PuckCriterion3D
介绍
Composite_PuckCriterion3D为3D状态下复合材料Puck失效准则。
原理
Puck准则被VDI和DNV规范引用,在过去50多年的发展中不断完善,由于目前大多数的工程软件只支持最早版本的puck准则,后续比如纤维失效中压缩效应的折减,纤维间失效系数的σ1削弱系数的引用都未提及,本文利用Matlab粗浅完善了后续Puck准则的相关进展,在本文编写的过程中得到了
Oliver博士 (https://ofcconsulting.de) 的帮助,在此表示感谢。
纤维失效准则
Puck 在 1969 年即提 出采用这个公式 [ Puck 1969, Puck 和 Schneider 1969] , 其物理意义就是 UD 层在多向应力作用下, 当平行于纤维方向的应力 σ1 等于或大于单轴应力作用下纤 维失效所需应力时, 纤维就发生了失效。 基于这种假设, 简单的纤维失效的条件为:
$$
\frac{\sigma_1}{R_∥^t}=1\quad\sigma_1>0
$$
$$
\frac{\sigma_1}{-R_∥^c}=1\quad\sigma_1<0
$$
当$\sigma_1$是拉伸应力,上式中$R_∥^t$为纤维失效拉伸强度。
当$\sigma_1$是压缩应力,上式中$R_∥^c$为纤维失效压缩强度。
Mannigel [ Mannigel 2007] 通过大量的试验研究来量化这 种影响。 他发现相对较小的剪切应力 $\tau_{21}$ 对纤维失效几乎没有影响。 如果剪切应力超过了临界值并导致微损伤, 压缩失效强度则会明显降低。 Mannigel 发现在临 界值以上剪切应力和压缩失效强度存在一个线性递减的关系。 这个关系通过发表在 [ Mannigel 2007] 上的大量试验结果来确定。
更新后的纤维压缩失效准则如下:
$$
f_{E,FF}^{(-)}=\frac{\sigma_1}{-R_∥^c}\quad\sigma_1<0\ and\ \abs {\frac{\tau_{w1}}{\sigma_1}}\le\frac{\tau_{21,thr}}{R_∥^{(-)}}
$$
$$
f_{E,FF}^{(-)}=\frac{(1-k)\sigma_1}{-R_∥^c}+\frac{\tau_{w1}}{R_{⊥∥}^A}\quad\sigma_1<0\ and\ \abs {\frac{\tau_{w1}}{\sigma_1}}>\frac{\tau_{21,thr}}{R_∥^{(-)}}
$$
式中:
$\tau_{21.thr}=kR_{⊥∥}^A$,一般可取k=0.5,该值在0~1之间,
$\tau_{w1}=\sqrt{\tau_{21}^2+\tau_{31}^2}$
纤维间失效准则
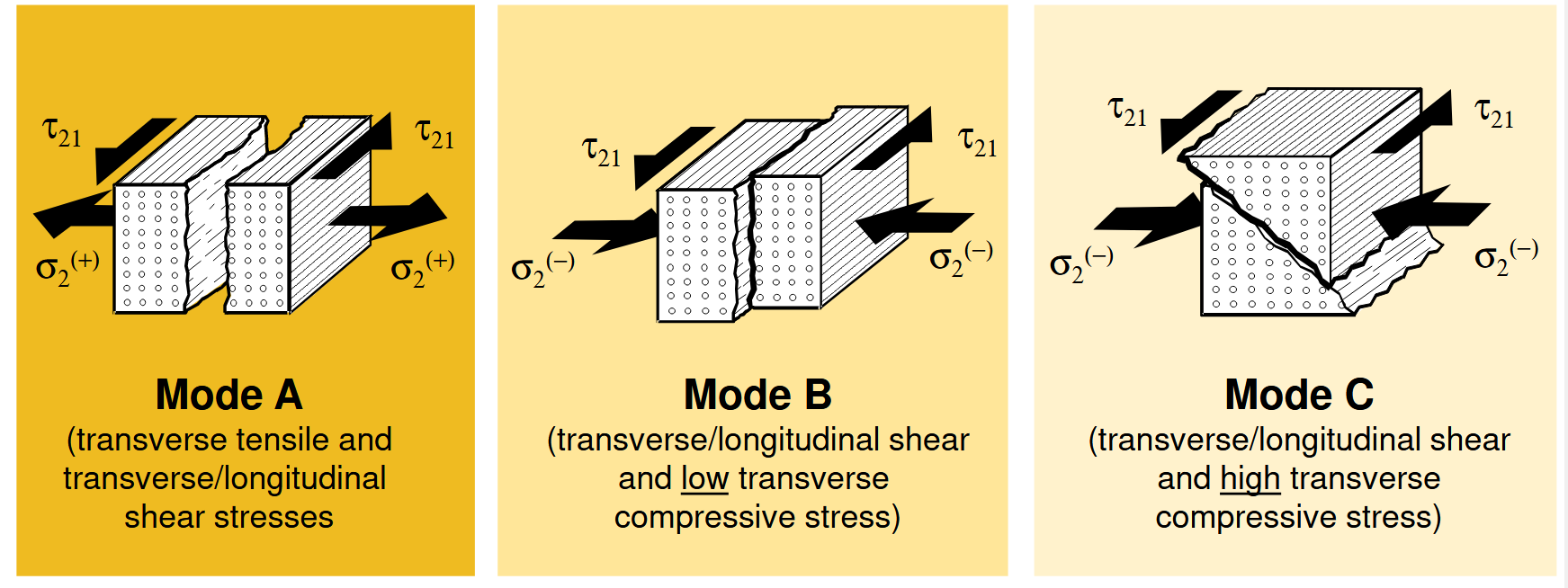
针对不同IFF断裂模式,主要有三种失效模式:
模式 A: 由横向拉伸应力 $σ_⊥^t$ 或纵向剪切应力 $\tau_{⊥‖}$ 单独作用或共同作用所 引起的失效。 在二维应力状态 σ1 、 σ2 、 $\tau_{12}$ 下, 裂纹沿着厚度方向扩展, 因此在 由 σ2 和 $\tau_{12}$ 共同作用面上扩展。 由于拉伸应力作用, 断裂面彼此分离。 从宏观上 分析, 这会导致弹性模量 $E_⊥$和剪切模量 $G_{⊥‖}$的下降。
模式 B: 失效由纵向剪切应力 $\tau_{⊥‖}$引起的。 这种失效发生在外部剪切应力$\tau_{12}$ 作用的平面上。 与模式 A 相比, 和 $\tau_{⊥‖}$共同作用在失效面上的横向正应力 $σ_⊥^c$ 是压缩应力。 其裂口不会张开并且断裂面会相互挤压在一起。 因此 IFF 模式 B 引 起的刚度下降明显低于 IFF 模式 A 引起的刚度下降。 因此, 只有断裂面的压缩应 力与横向压缩强度比值 $\abs{σ_{⊥fr}^c / R_⊥^c}$ 小于 0. 4 时, IFF 模式 B 才会发生。
模式 C: 如果失效处的压缩应力与横向压缩强度比值$\abs{σ_{⊥fr}^c / R_⊥^c}$大于 0. 4 时, 外部剪切应力 $\tau_{12}$ 作用面就不再是断裂面。 事实上, 失效发生在与 σ2 和 $\tau_{21}$ 作 用面成角度为 θfp ≠0° 的斜面上。 在平面应力状态下, 失效角的增加从模式 B 到模式 C 的临界值 0°到大致 54° 再到纯粹横向压缩应力 ( $\tau_{21}$ = 0) 。 IFF 模式 C 意味着在破坏层和相邻层之间存在着分层的危险。
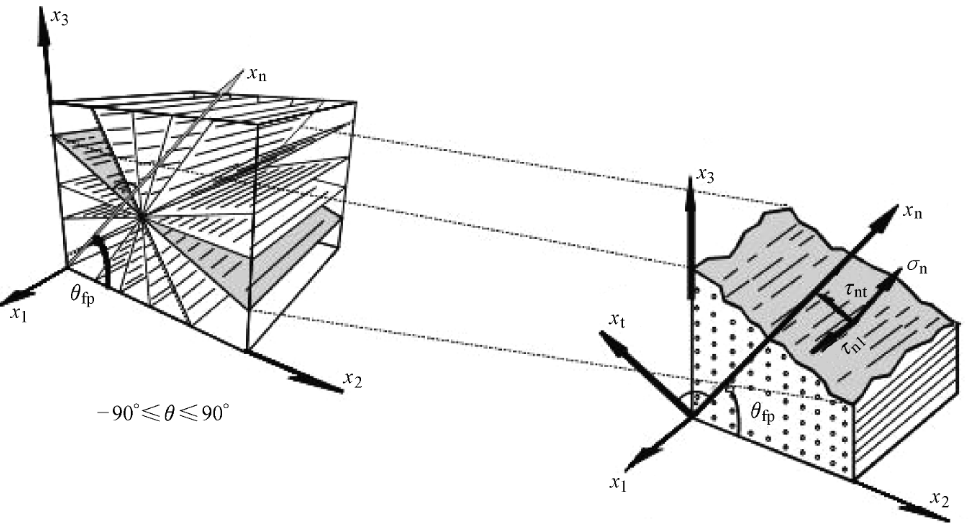
当计算IFF失效时,首先需要在-90°~90°之间建立关键平面,将计算所得的平面投影到该平面,通常以1°为步长,进行180次计算,在由如下公式计算该角度平面的系数,最终汇总180个结果,取其最大值。
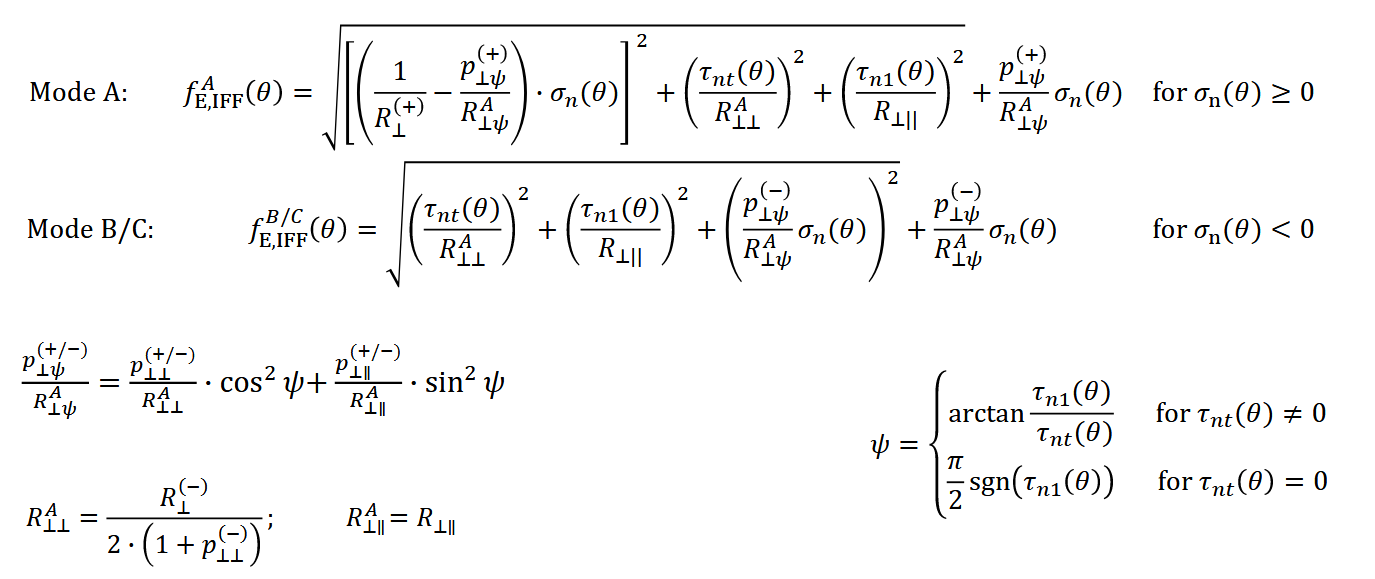
这里还涉及一个倾角参数的选取,针对GFRP和CFRP可以选用如下参数:

DNV$^{[2]}$规范则给了一个相对折中的值,个人感觉该值在GFRP材料中还是有一定的参考意义
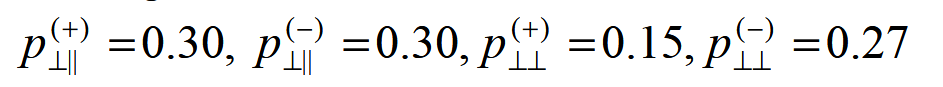
根据莫尔假设, 平行于纤维方向的应力σ1 对 IFF 都没有任何影响, 由于σ1 的作用面垂直于应力σn 、 n1 和 nt 的作用面, 应力σn 、 n1 和 nt 对于 IFF 具有决定 性意义。 但是, 一系列影响的出现使得有必要在 IFF 准则中包含σ1 项, 这将稍微 降低 IFF 强度 [ Puck 1996] 。
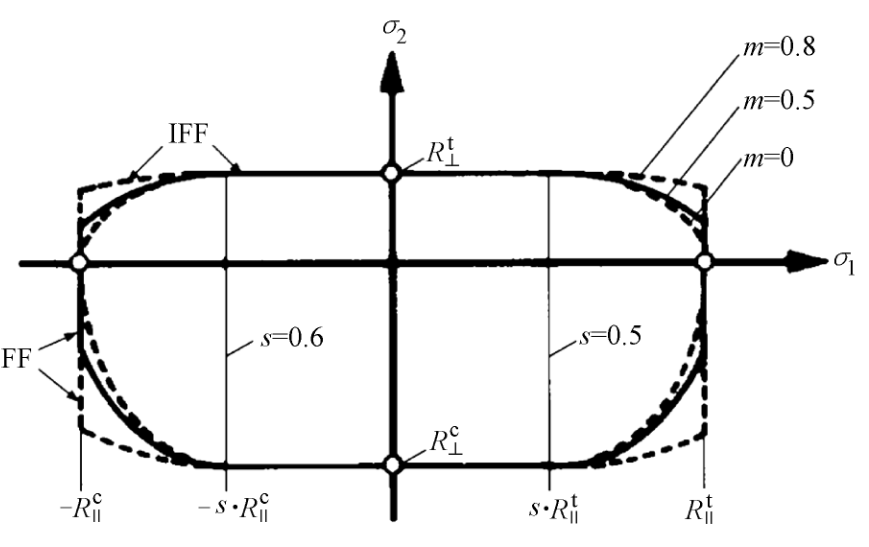
为了在 IFF 分析中以适合于实际情况的方式包含来自σ1 的弱化效应, 通过一 作用面的抗断裂性$R_⊥^t$、 $R_{⊥⊥}^t$ 和$R_{⊥‖}$ 乘以一个折减系数$η_{w1}$:
$$
f_{E1}=\frac{f_{E0}}{\eta_{w1}}
$$
在给定的假设下,推导折减系数$\eta_{w1}$的公式:
$$
\eta_{w1}=\frac{c[a\sqrt{c^2(a^2-s^2)+1}+s]}{(ca)^2+1}
$$
其中,$c=\frac{f_{E0}}{f_E(FF)}$,$a=\frac{1-s}{\sqrt{1-m^2}}$
渐进损伤
Puck准则同样也适用于渐进损伤分析,其通过大量的试验确定了$E_⊥$和$G_{⊥∥}$与危险系数之间的关系:
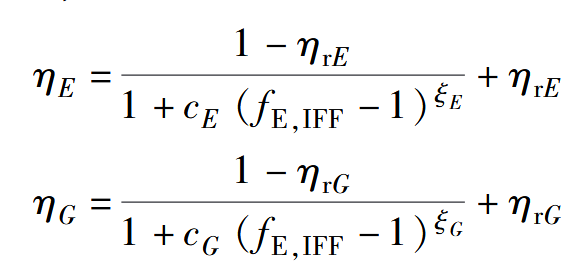
Knops 为了验证后失效分析模型做了大量的工作以提供实验数据 [ Knops 2003] 。可参考以下参数取值。
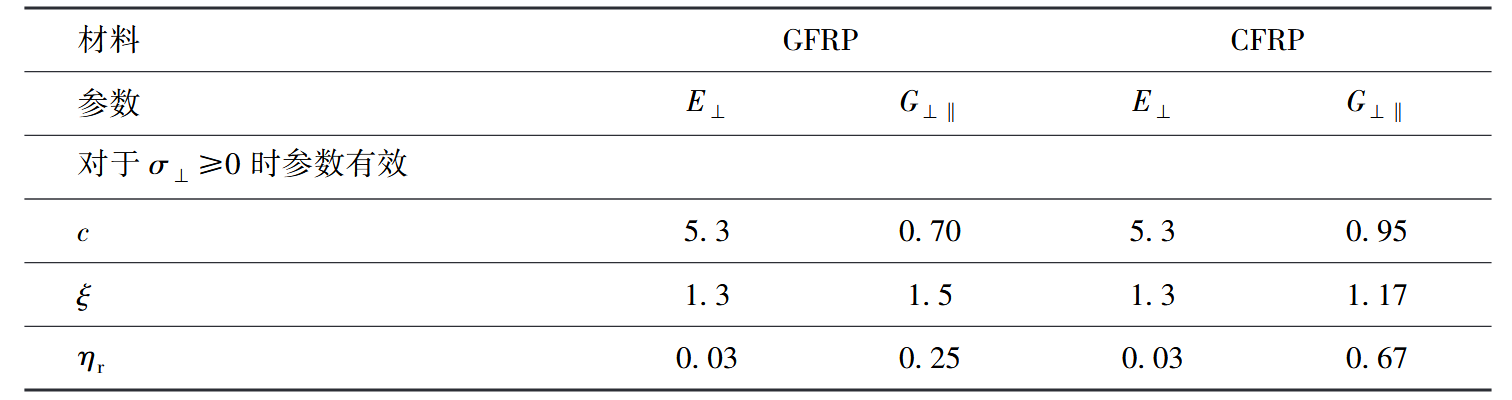
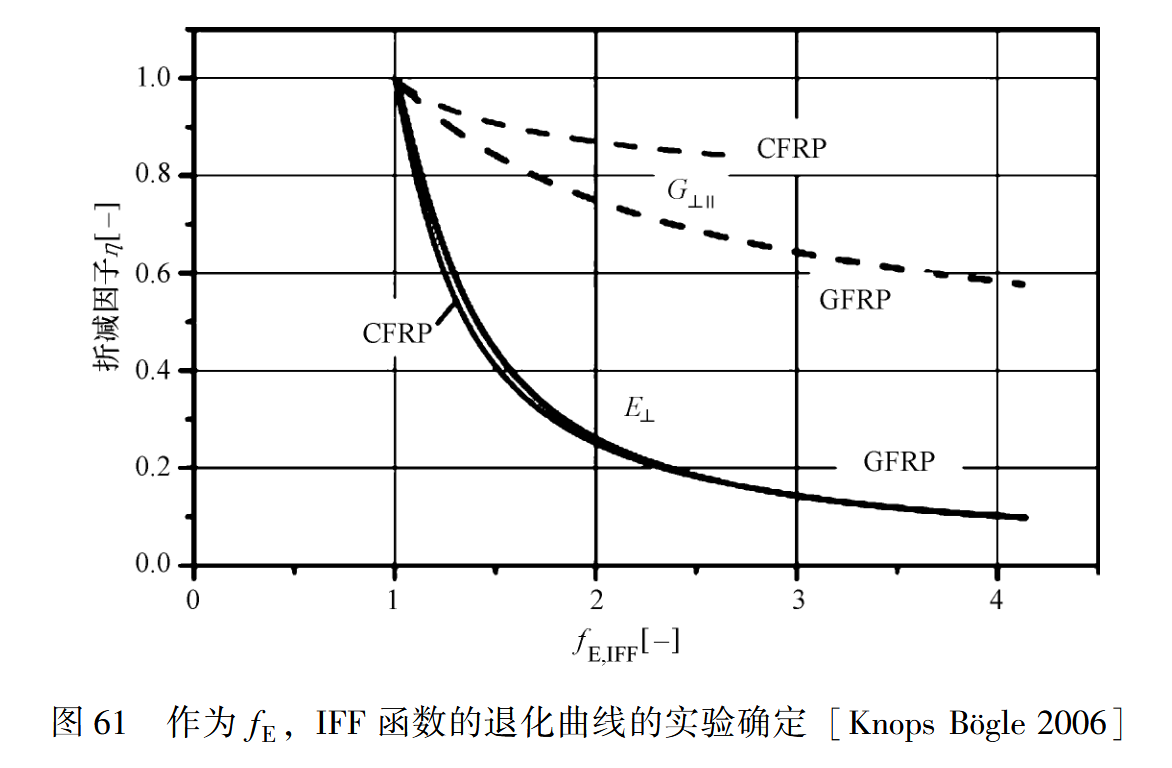
类结构
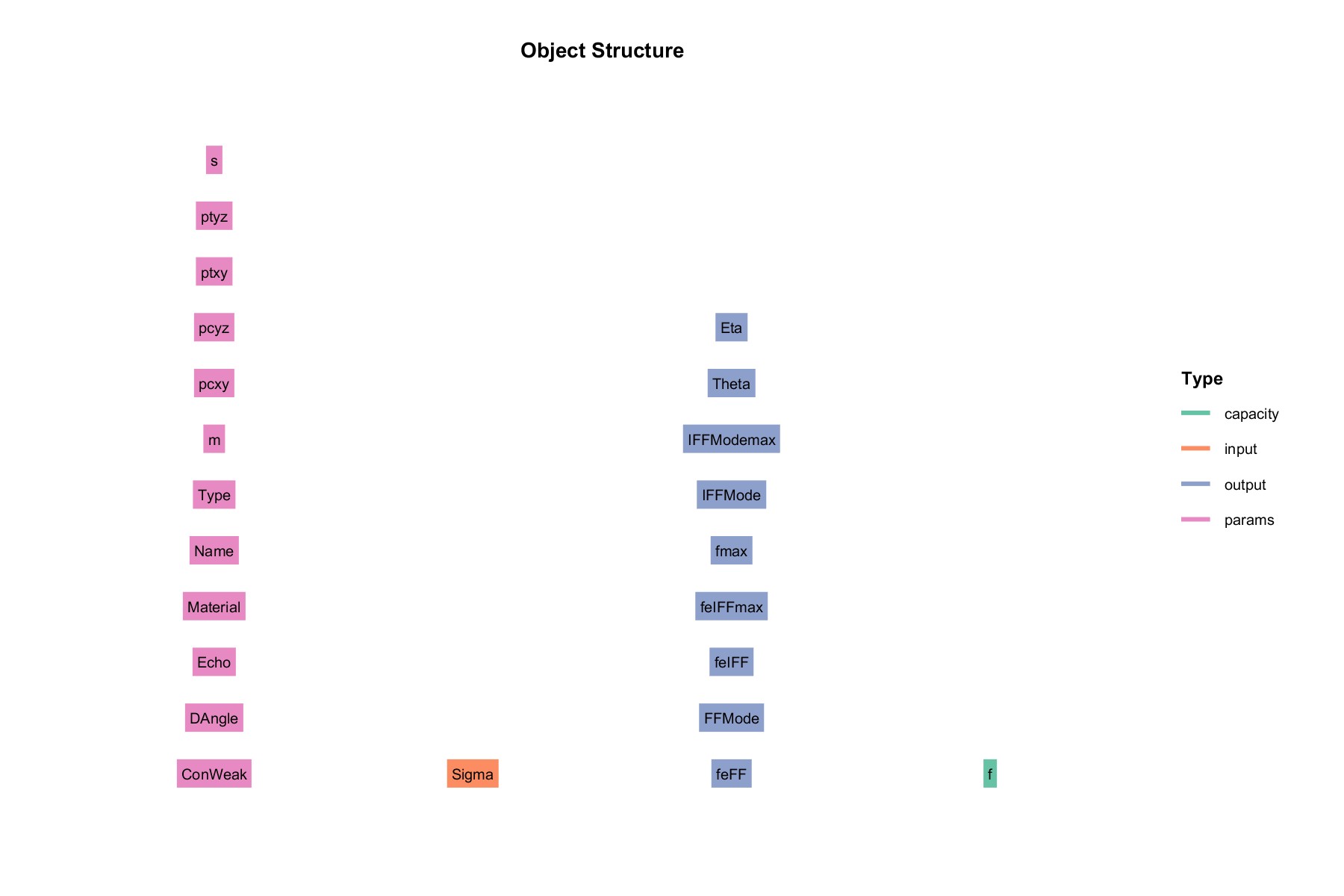
输入 input:
- Sigma : 应力
参数 params:
- s :σ1折减系数参数
- ptyz : 倾角参数
- ptxy : 倾角参数
- pcyz : 倾角参数
- pcxy : 倾角参数
- m : σ1折减系数参数
- Type : 材料类型
- Name : 名称
- Material : 材料属性
- DAngle : 角度步长
- ConWeak : 考虑σ1折减
输出 output :
Eta :折减系数
Theta : 失效平面角度
IFFModemax : IFF失效模式
IFFMode :IFF失效模式
fmax : 危险系数最大值
feIFFmax: IFF失效危险系数
feIFF: IFF失效危险系数
FFMode :FF失效模式
能力 capacity :
- f : 安全系数
案例
S=RMaterial('Composite');
Mat=GetMat(S,34);
inputStruct1.Sigma=[-36.2315,160.745,-3.07,0,0,0;...
2099.75,38.757,-2.3,0,0,0;...
-36.559,158.08,-1.6742,0,0,0;...
2057.85,38.3085,-1.29,0,0,0];
paramsStruct1.Material=Mat{1,1};
paramsStruct1.DAngle=1;
paramsStruct1.ConWeak=0;
paramsStruct1.Type='CFRP';
% paramsStruct1.Type='GFRP';
paramsStruct1.s=0.5;
paramsStruct1.m=0.5;
C= method.Composite.PuckCriterion3D(paramsStruct1, inputStruct1);
C= C.solve();
PlotEtaCurve(C);
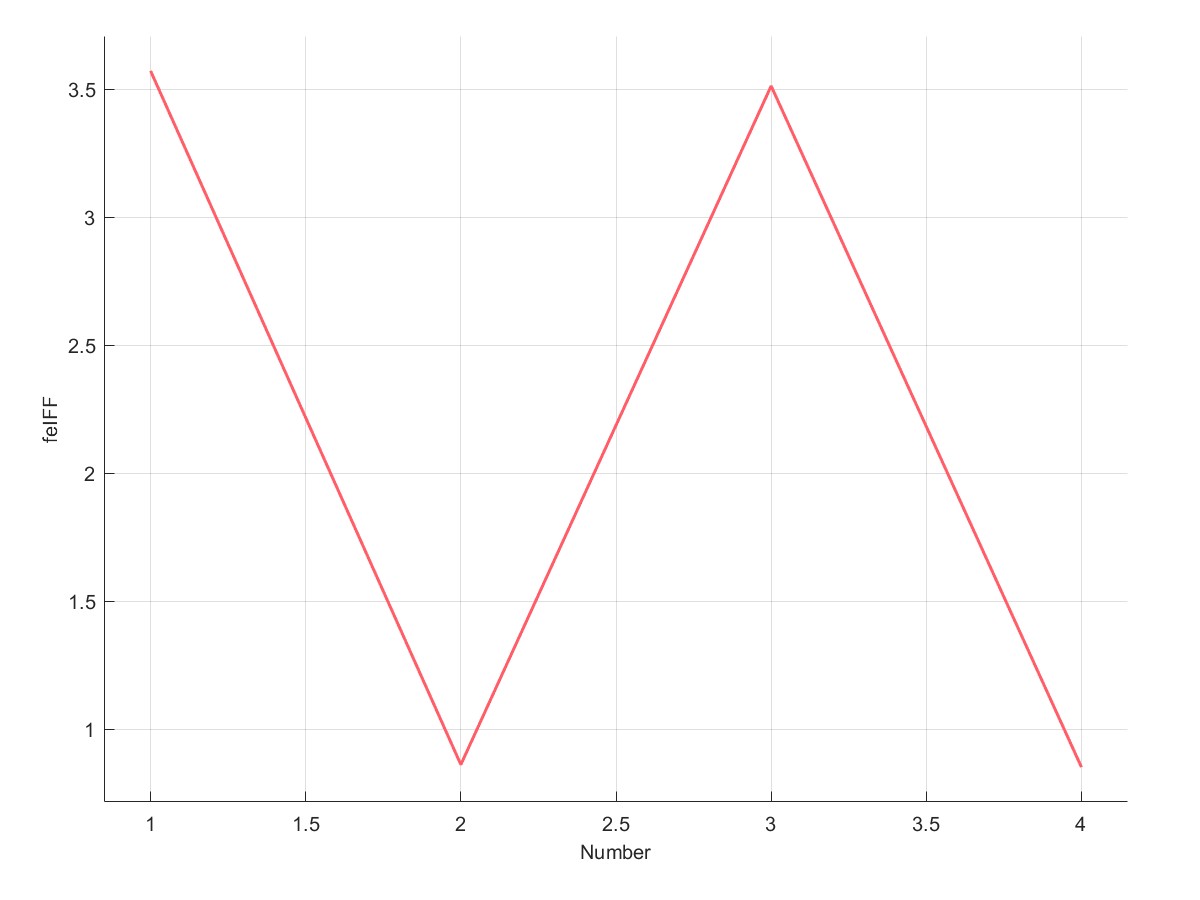
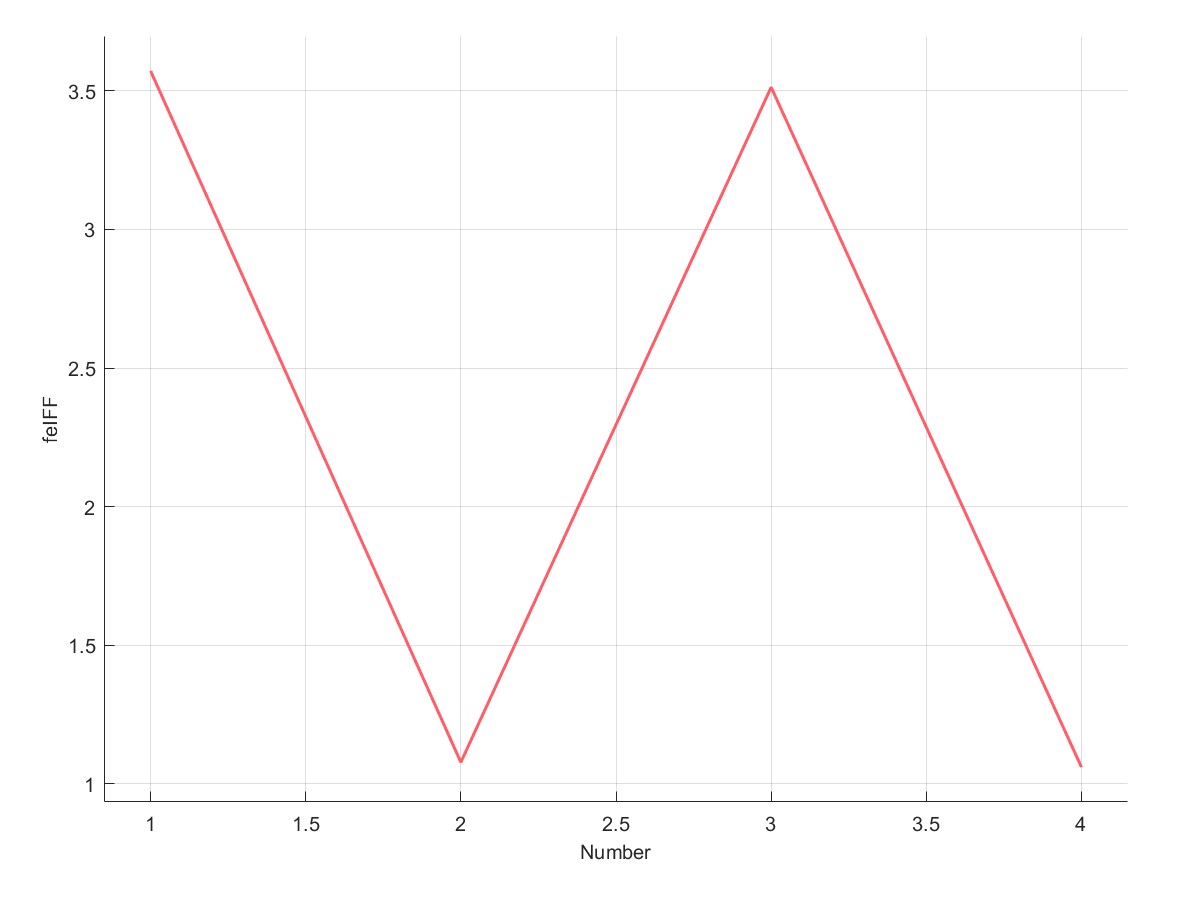
PlotfeIFF(C);
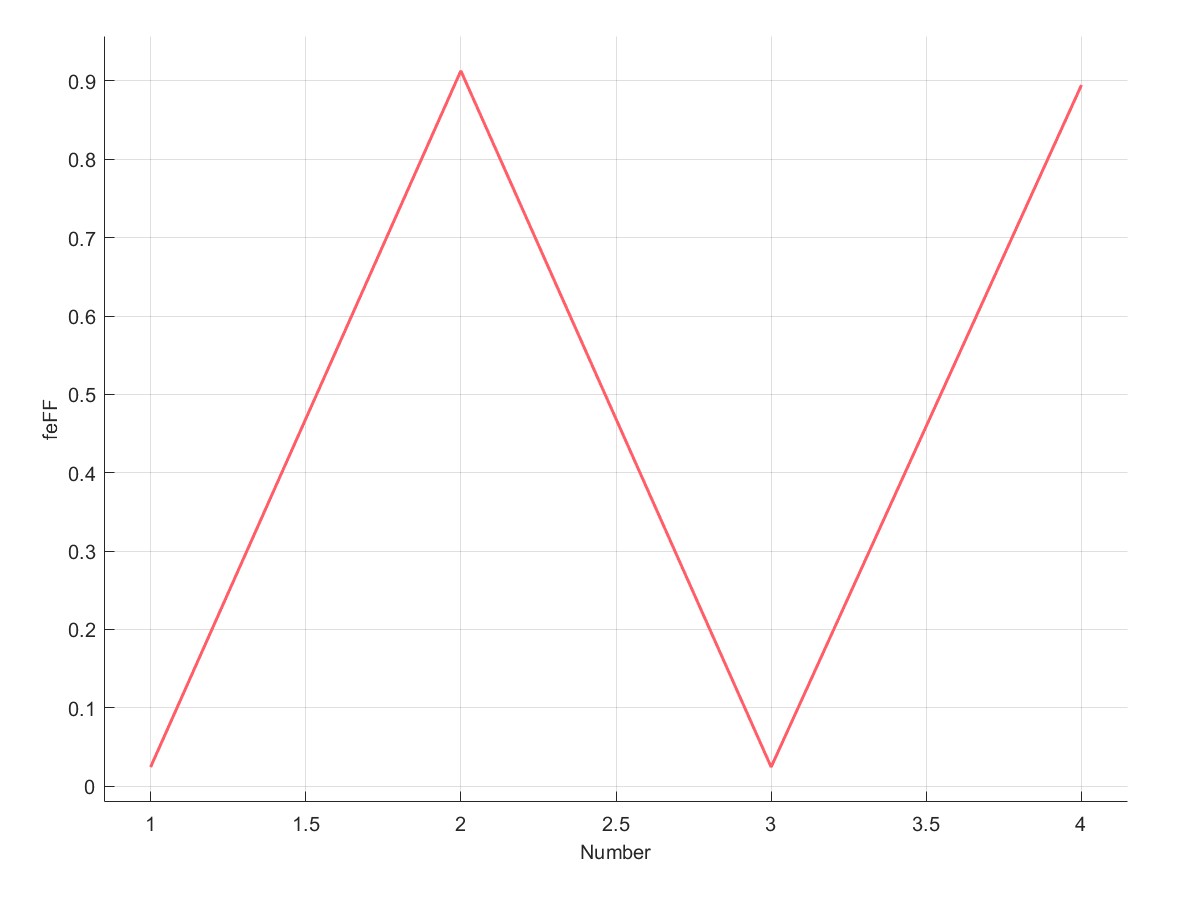
PlotfeFF(C);
PlotfeIFFmax(C);
PlotfeIFFTheta(C);
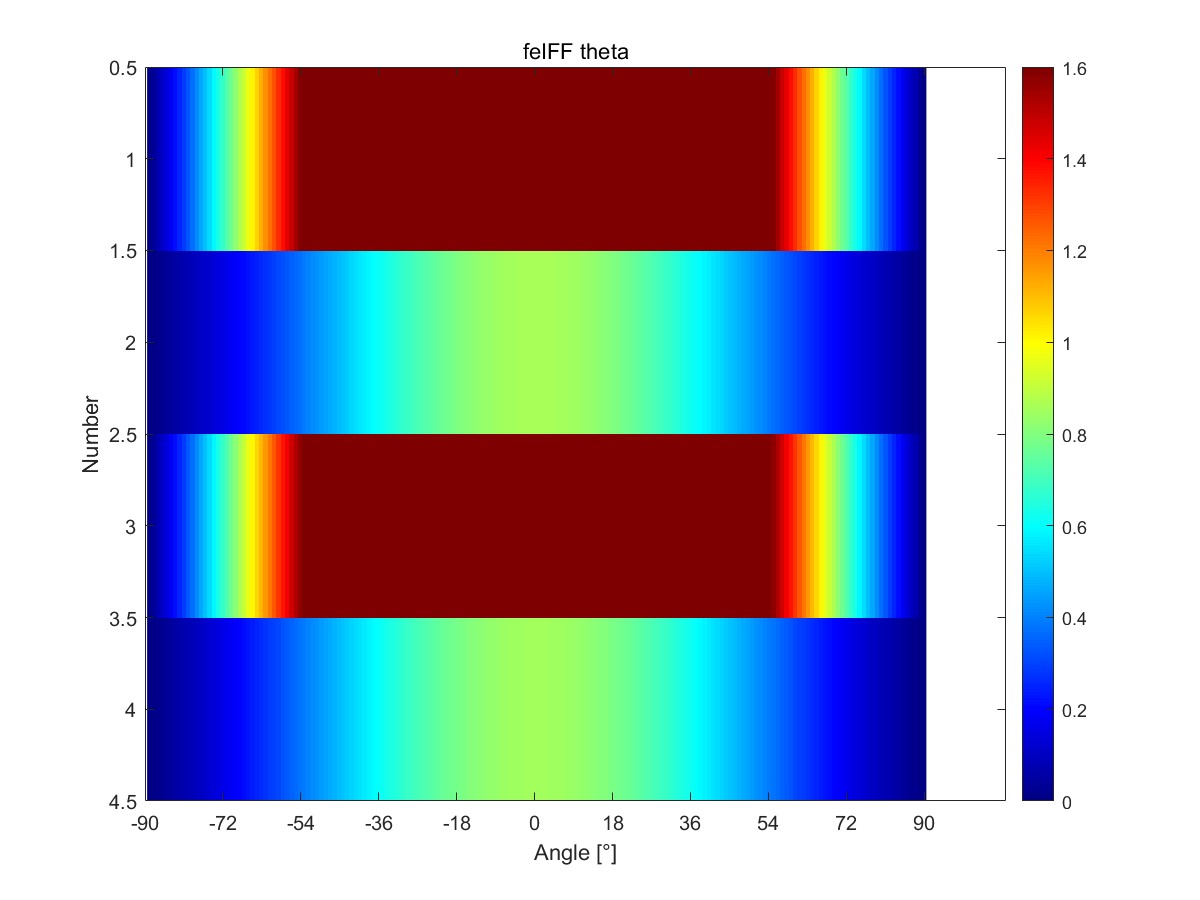 | 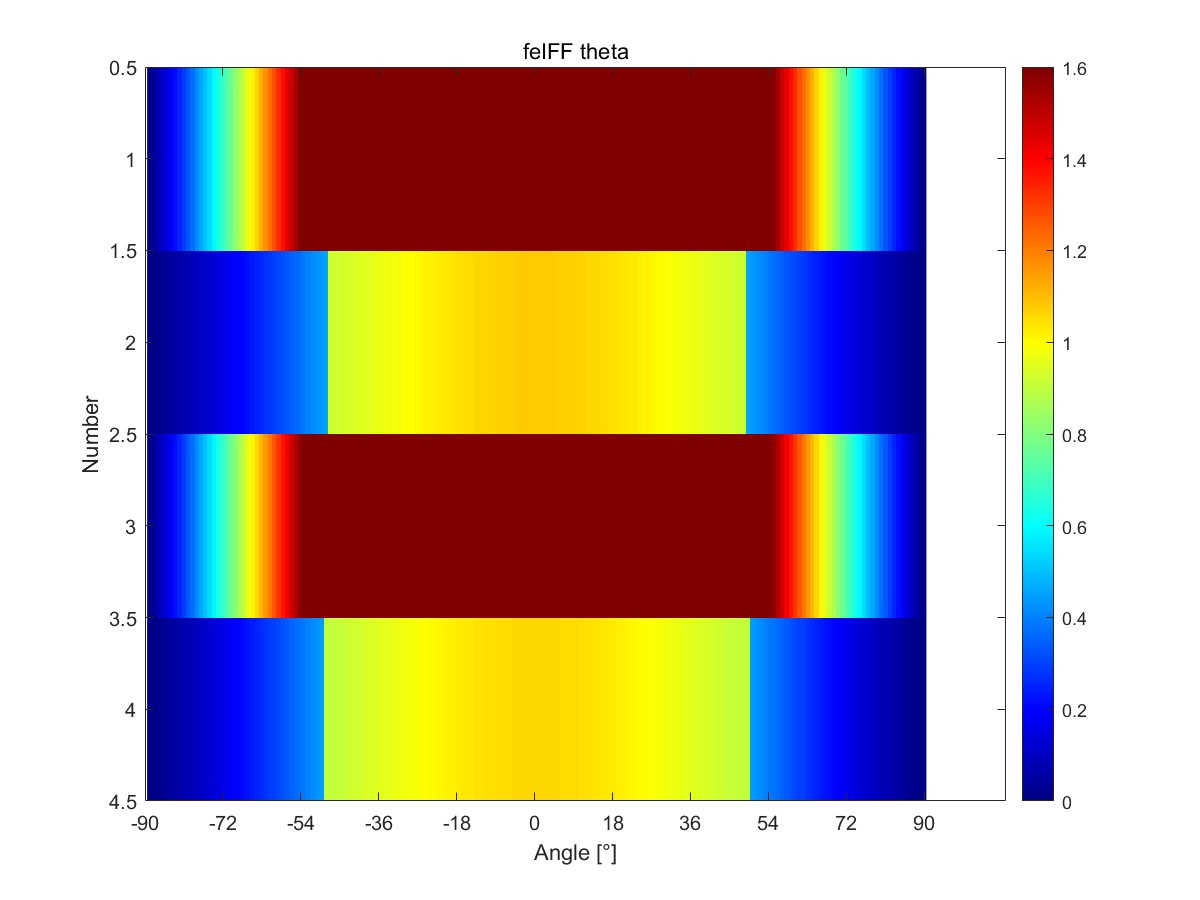 |
| 不考虑σ1折减 | 考虑σ1折减 |
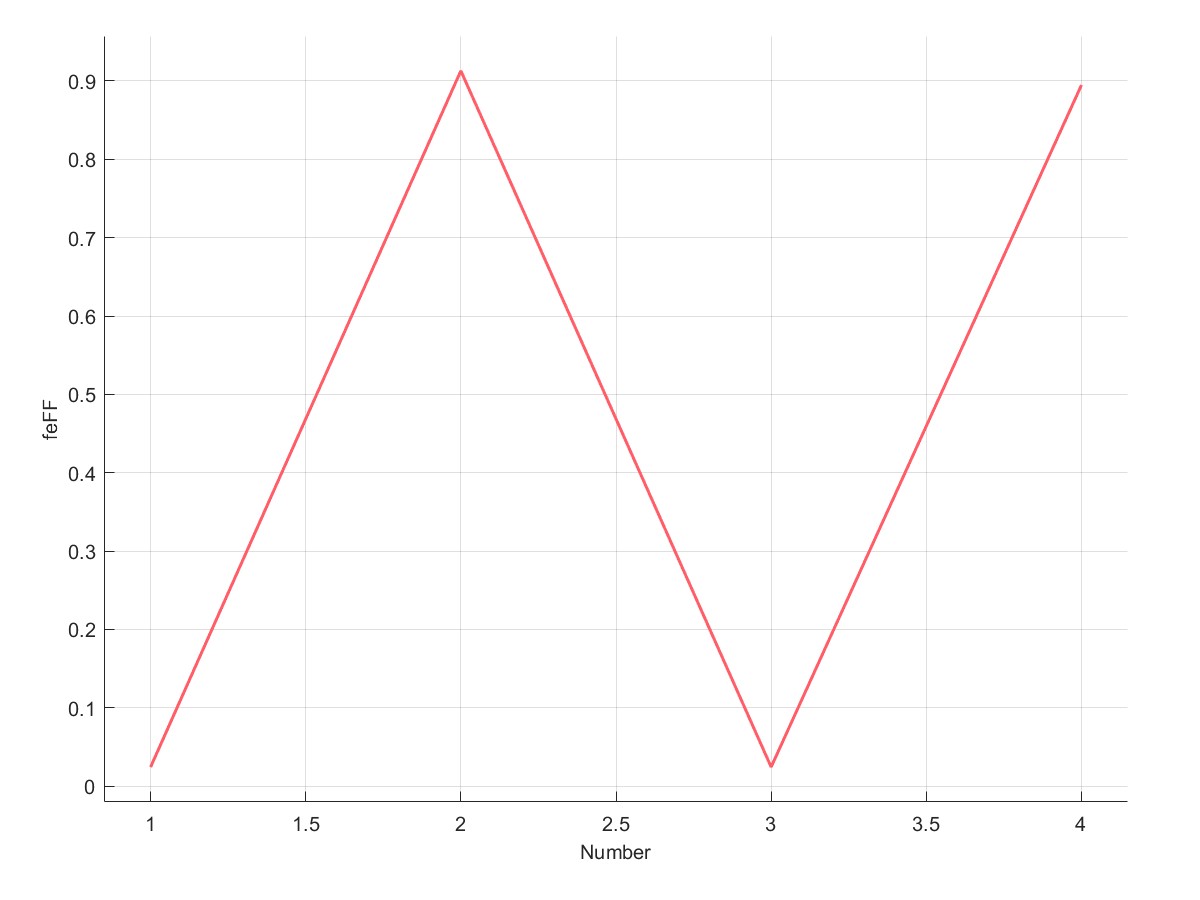 |  |
| 不考虑σ1折减 | 考虑σ1折减 |
 |  |
| 不考虑σ1折减 | 考虑σ1折减 |
 |  |
| 不考虑σ1折减 | 考虑σ1折减 |
同时在材料强度不变的情况下,变更材料类型由CFRP为GFRP,可观察两者折减系数取值的区别
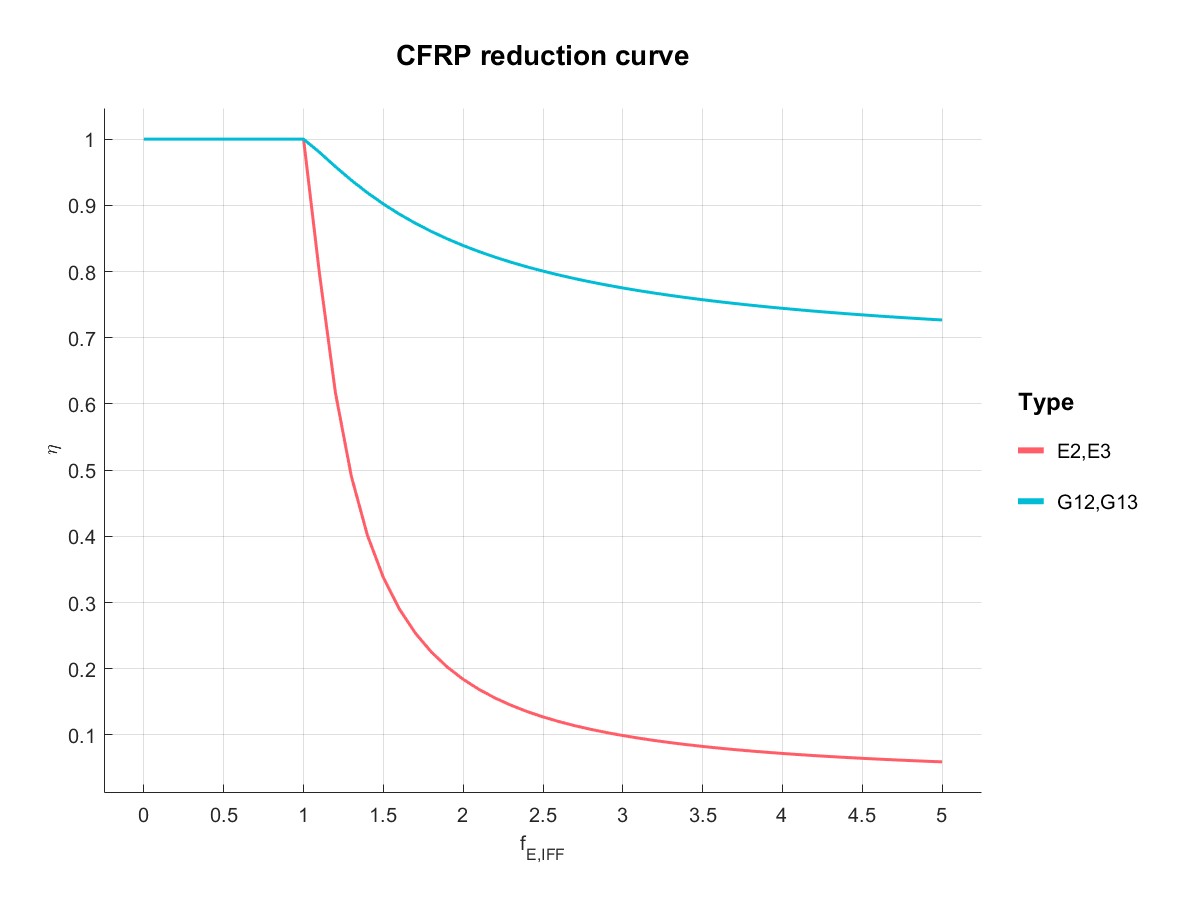 | 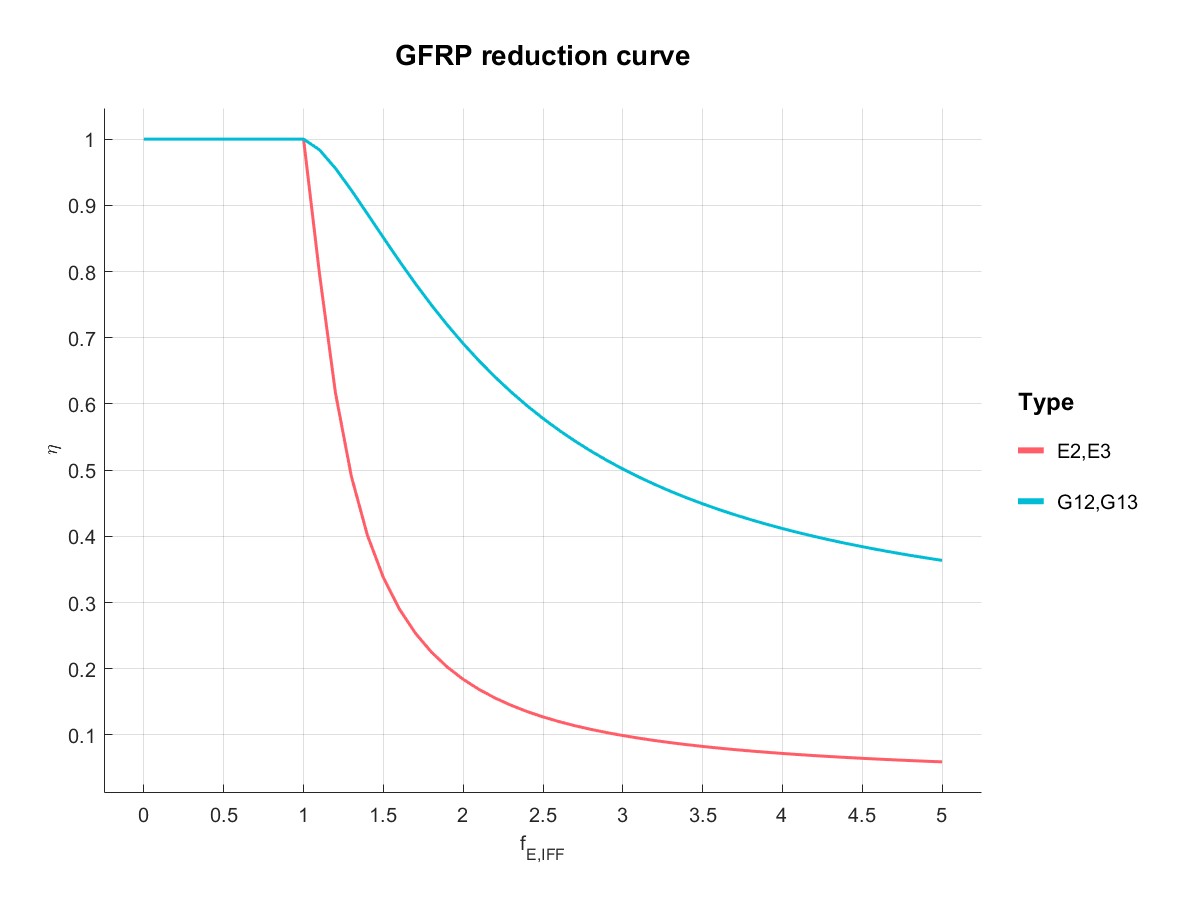 |
| CFRP | GFRP |
CFRP计算得到的折减系数:
0.0799778409034907 0.755288692029387
1 1
0.0814442969222847 0.757023702971999
1 1
GFRP计算得到的折减系数:
0.0807882284717462 0.442922535823326
1 1
0.0822655919265399 0.447971787610760
1 1
参考文献
[1] 复合材料层合板失效分析
[2] DNV-OS-C501
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com