Mori-Tanaka方法与微观力学分析

Mori_Tanaka方法

1973年，Mori和Tanakal在研究弥散硬化材料的加工硬化时，提出求解材料内部平均应力的背应力方法，即Mori-Tanaka法。由于这个方法运算简单，同时在一定程度上考虑了复合材料中夹杂相之间的相互作用，近年来受到广泛的应用，成为处理各种非均质复合材料性能的有效手段之一。

具体说明可参考文献[1]，本文仅给出最终的公式

纵向弹性模量

纵向弹性模量可由下式计算：
$$
\frac{E_{1}}{E_0}=\frac{1}{1+V_f[A_1-v_0(A_2+A_3)]/A}
$$

横向弹性模量

$$
\frac{E_{2}}{E_0}=\frac{1}{1+V_f[A_5-v_0(A_4+A_6)]/A}
$$

纵向剪切模量

$$
\frac{G_{12}}{G_0}=1+\frac{V_f}{2(1-V_f)S_{1212}+G_0/(G_1-G_0)}
$$

纵向泊松比

$$
v_{12}=\frac{v_0-V_f[A_4-v_0(A_5+A_6)]/A}{1+V_f[A_1-v_0(A_2+A_3)]/A}
$$

横向泊松比

$$
v_{23}=\frac{v_0-V_f[A_6-v_0(A_4+A_5)]/A}{1+V_f[A_9-v_0(A_7+A_8)]/A}
$$
以55%体积率的玻璃钢复合材料为例，采用MT方法预测材料属性随体积率变化如下：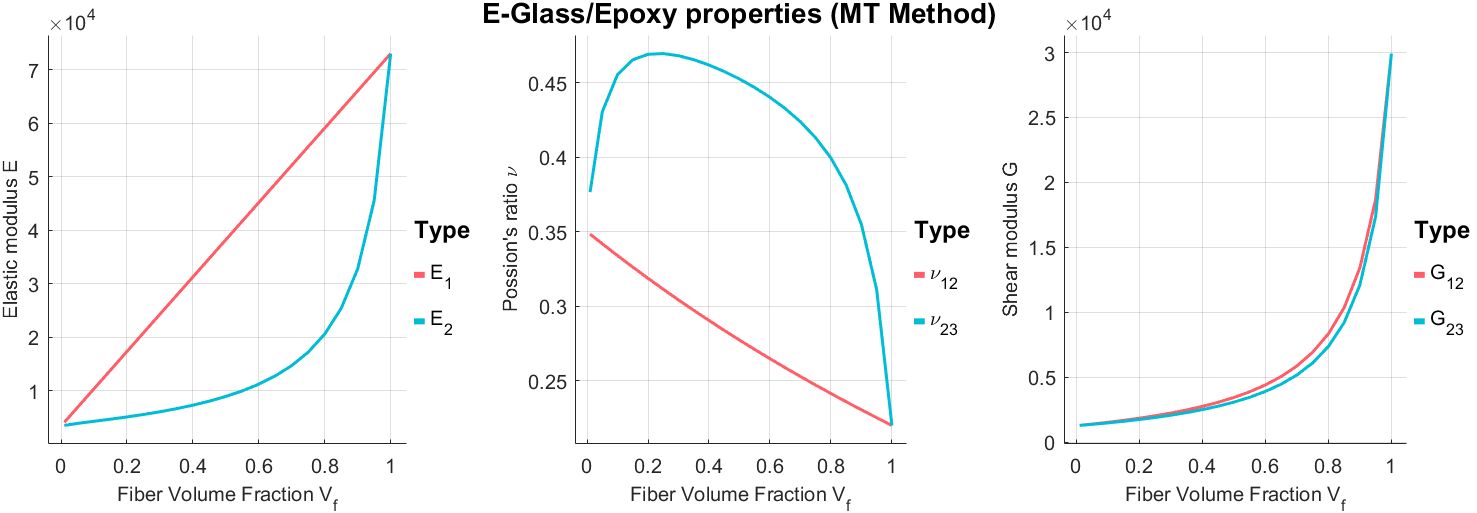

S=RMaterial('Composite');
mat=GetMat(S,[1,2]');
inputStruct.Vf=0.55;
inputStruct.Fiber=mat{1,1};
inputStruct.Matrix=mat{2,1};
paramsStruct.Theory='MT';
Ply1= method.Composite.Micromechanics(paramsStruct, inputStruct);
Ply1=Ply1.solve();
Plot(Ply1);
PlotAlpha(Ply1);

微观力学分析

在微观力学模型中，建立相同体积率的模型，参见Micromechanics模块，图中蓝色为Eglass, 黄色为环氧树脂Epoxy。

通过分析其应力和应变，也可以计算材料属性：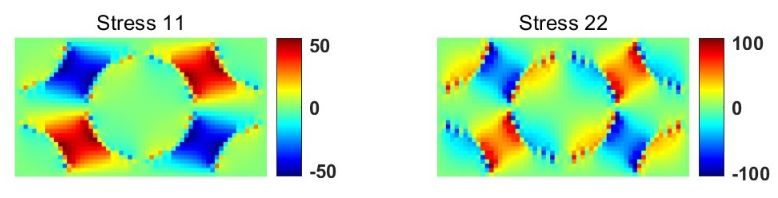

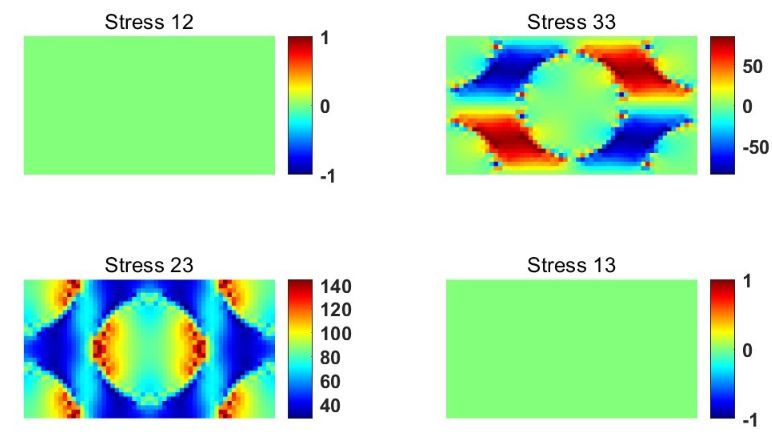
S=RMaterial('Composite');
mat=GetMat(S,[1,2]');
inputStruct.Vf=0.55;
inputStruct.Fiber=mat{1,1};
inputStruct.Matrix=mat{2,1};
inputStruct.Load.Type=[2,2,2,1,2,2];% 2-Stress 1-Strain
inputStruct.Load.Value=[0,0,0,0.02,0,0];
inputStruct.Load.NINC=400;
paramsStruct.RUCid=200;
paramsStruct.Theory='HFGMC';
paramsStruct.Damage=0;% Progressive damage analysis
paramsStruct.Criterion=0; % Failure criterion
Ply2= method.Composite.Micromechanics(paramsStruct, inputStruct);
Ply2=Ply2.solve();

两者对比，可以发现材料力学属性十分接近。

	MT	Micro
E1	41.7	41.5
E2	10	11
E3	10	10.5
v12	0.27	0.27
v13	0.27	0.27
v23	0.45	0.42
G12	3.89	4.03
G13	3.89	3.83
G23	3.46	3.66
相比较而言，可以采用经验公式的算法，速度更快，采用微观力学的方式除了获得材料的属性外，也可以获得更多的信息，比如应力、应变以及渐进损伤分析等。因此，对于复合材料来说，遇到一些棘手的问题，通常可求助微观力学来寻求答案。

参考文献

[1] 三维编织复合材料力学性能分析方法
[2] Practical micromechanics of composite materials
[3] https://www.feacat.com/2025/05/06/Composite_Micromechanics/

---

本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com