渐进损伤分析
通常情况下,复合材料纤维的断裂可以认为是结构的破坏。但层间或者树脂基底的破坏,在有些情况下,结构依然能保持完好的功能性,这部分损伤被认为是可允许的损伤。比如一些压力容器内部,虽然有裂纹,但纤维仍然附着其表面,并没有丧失承载力,这些细微的损伤并没有对结构产生破坏。
这种效应通常需要通过渐进损伤分析来判断,根据有限元结果,对弹性模量和剪切模量$E_⊥$、 $G_{⊥‖}$进行折减,通过数次迭代来判断损伤是否收敛稳定。
应用Puck准则进行渐进损伤分析
根据 Puck 于 1969 年最初设计的退化方法 , 模量$G_{⊥‖}$ 、$E_⊥$ 和$v_{⊥‖}$:
$$
\eta_E=\frac{1-\eta_{rE}}{1+c_E(f_{E,IFF}-1)^{\xi_E}}+\eta_{rE}
$$
$$
\eta_G=\frac{1-\eta_{rG}}{1+c_G(f_{E,IFF}-1)^{\xi_G}}+\eta_{rG}
$$
$$
\eta_v=\frac{1-\eta_{rv}}{1+c_v(f_{E,IFF}-1)^{\xi_v}}+\eta_{rv}
$$
式中$\eta_r$、$c$、$\xi$均为试验拟合的参数,$f_{E,IFF}$为计算得到的层间失效的危险系数,大于1为失效。
有意思的一点是,这里有一个前提,不管你的失效模式是什么样,只要你的计算得到的危险系数一样,折减因子也一样。这点如果更现代的微观力学角度来说是有待斟酌的。
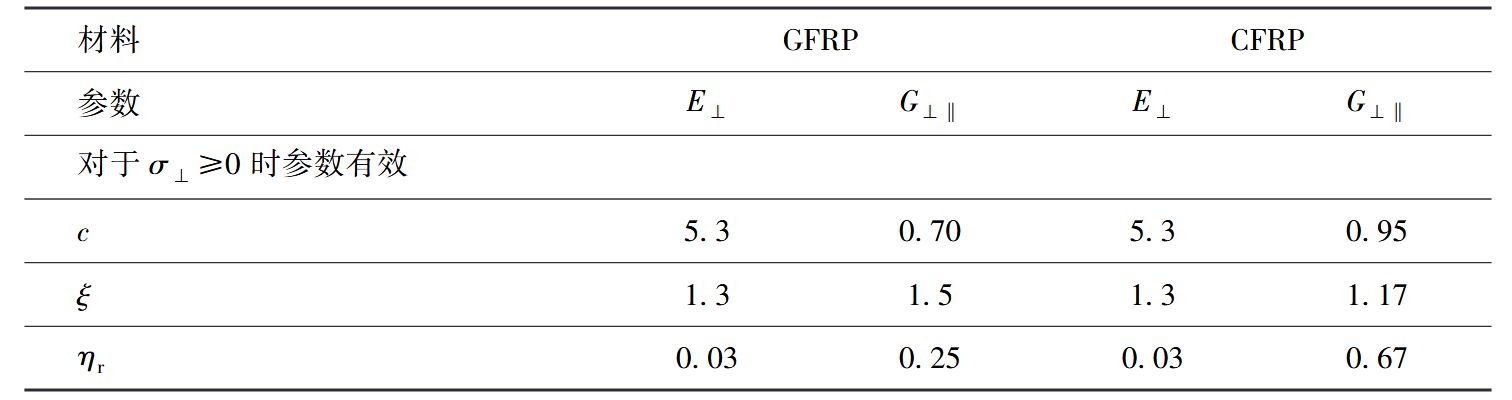
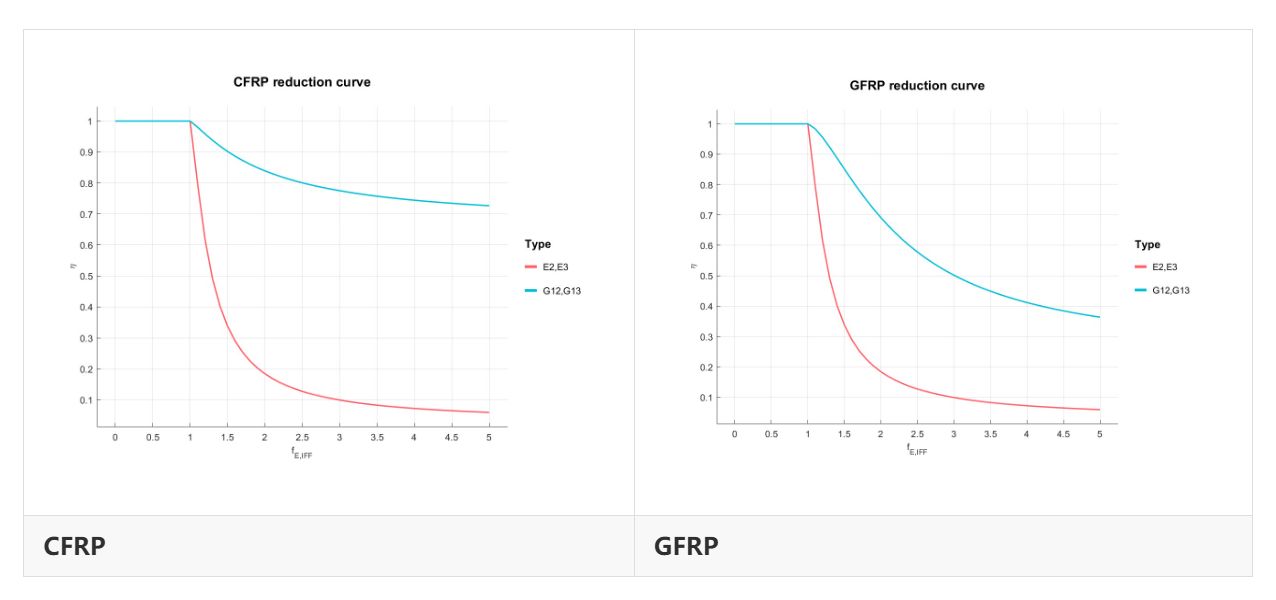
Knops于2003年的分析中,具体给定了拟合的参数,其结果表明 断裂力学方法模拟结果和实验数据都显示在给定的裂纹密度 (和给定的应力危险系数) 下, $E_⊥$的退化程度大于 $G_{⊥‖}$, 而泊松比 $ν_{⊥‖}$根本不需要折减 。因此在采用puck准则进行渐进损伤分析中无需对泊松比折减,笔者在测试有限元过程中,也发现即使泊松比发生变化,结果影响也很小。
对于CFRP和GFRP可按下表选取,可以发现两种材料对弹性模量的折减接近,对剪切模量的折减相差比较大。
有限元结果的修正
当对有限元结果进行修正时,给定一个载荷,计算得到的$f_{E,IFF}=1.5$,按照1.5去计算折减系数,再带入下一步计算。
这个时候又会发现一个bug,线弹性分析得到危险系数为1.5的时候,意味着这个结构很早之前就已经发生了变化,按照1.5系数得到的折减系数,并不是真正的折减系数,需要回退到安全系数为1时的情况重新计算。
一种比较简单的方式,就是缩小载荷步,比如原先10步的计算,改到100步,用微分的方式来近似分析。
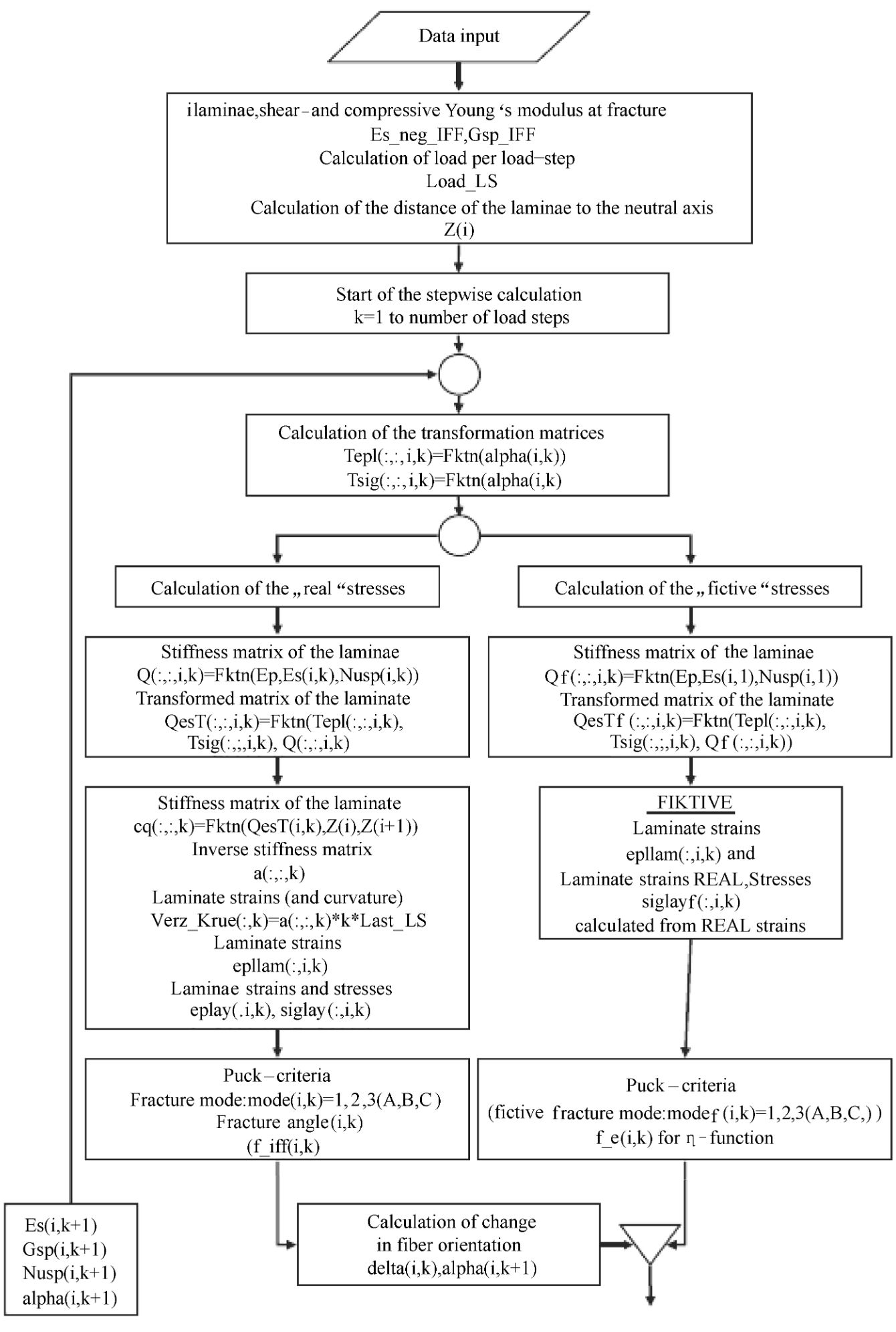
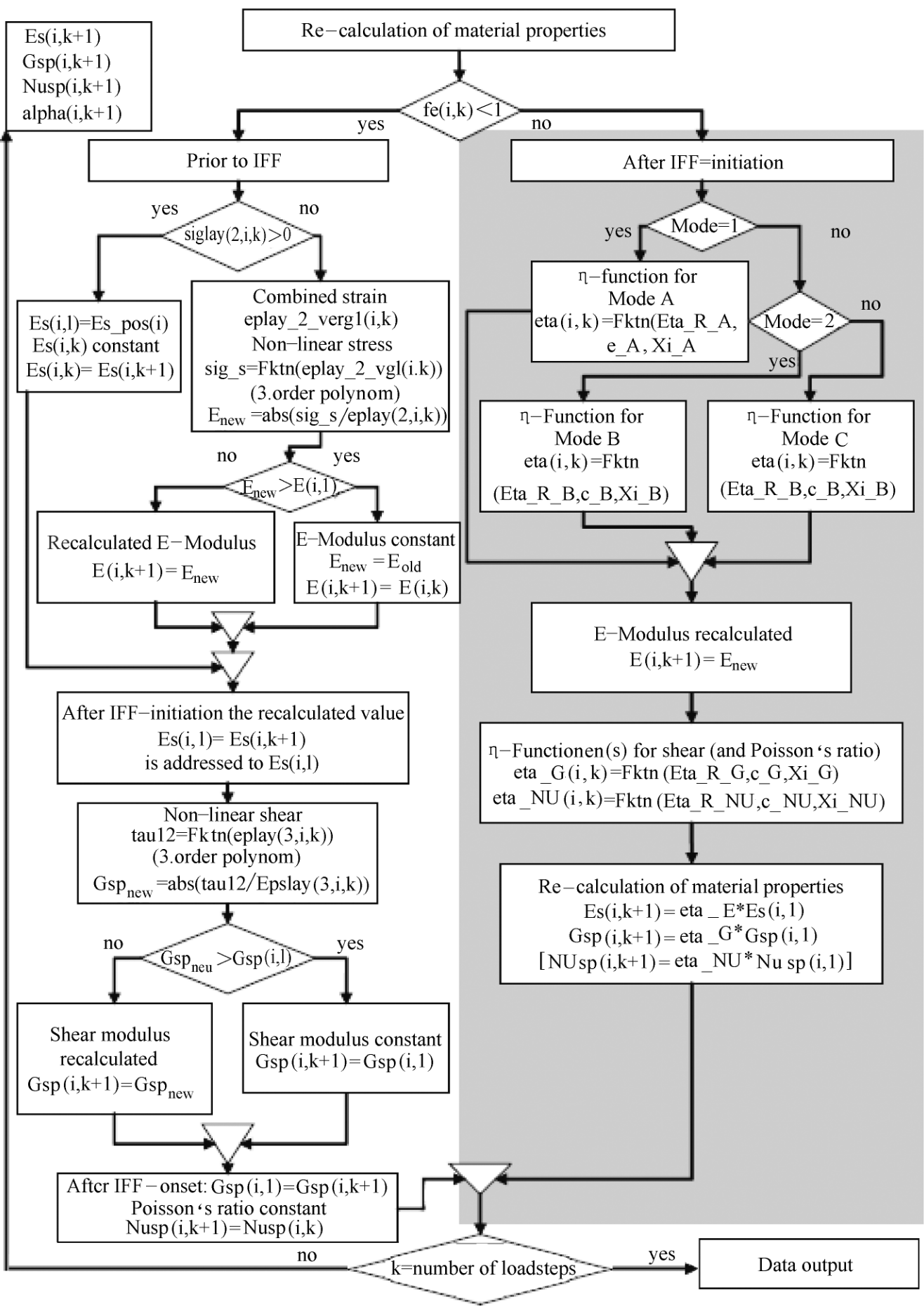
Knops提到了另一种方式,他将计算得到的应力分为两种,一种叫真实应力,一种时虚假应力,当通过第一步计算得到折减系数后,不能直接带入下一步,需要将第一步的应变带入折减后的结构,重新进行计算。如果危险系数小于1,则重新取该步的结果,该单元无需考虑折减。通过循环往复的迭代,可以得到最终的渐进损伤分析的结果。
参考文献
[1] https://www.feacat.com/2025/06/12/PuckCriterion3D/
[2] 复合材料层合板失效分析
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com