赫兹接触
在齿轴计算和仿真中,赫兹接触是一个比较关键的问题,这也是弹性力学研究的重要问题
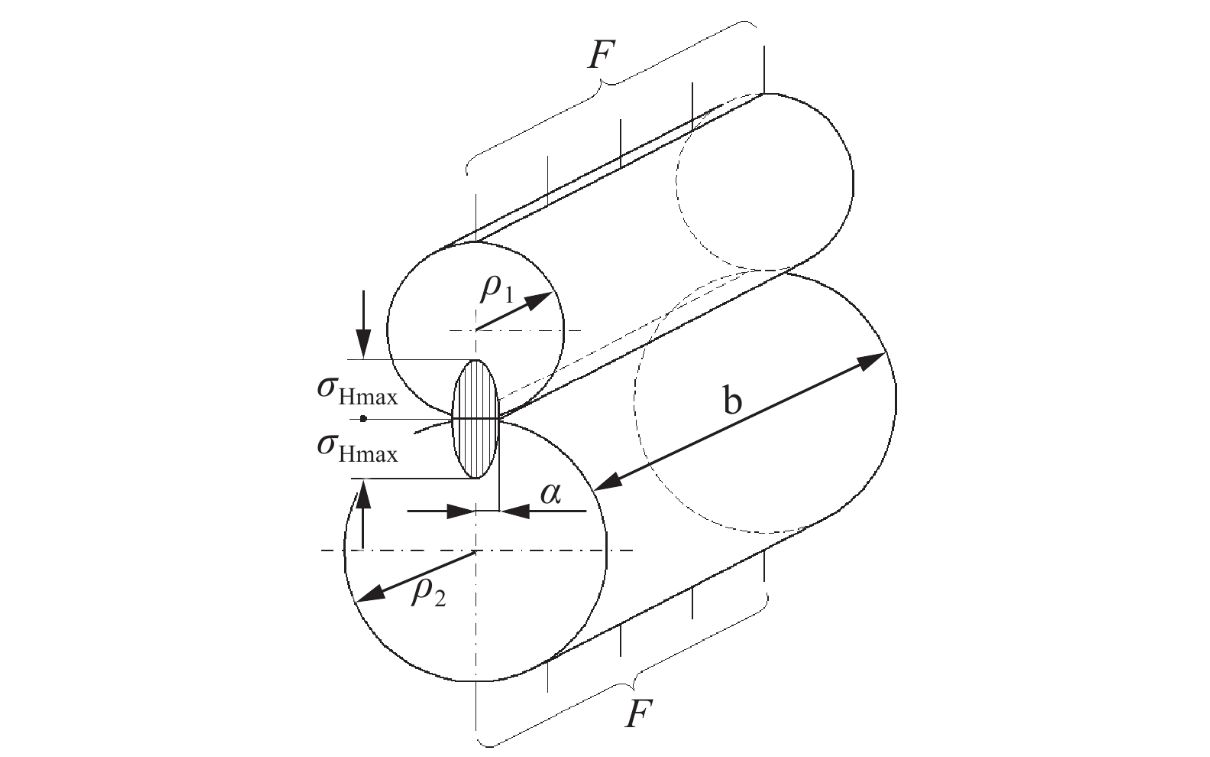
如图所示半径为r1和r2的两个圆柱体接触,其接触半宽a:
$$
a=\sqrt{\frac{4F}{\pi b}\frac{\frac{1-\mu_1^2}{E_1}+\frac{1-\mu_2^2}{E_2}}{\frac{1}{\rho_1}+\frac{1}{\rho_2}}}
$$
最大接触应力$\sigma_{Hmax}$为
(好奇怪,公式识别不出来,找不到bug,别的平台没问题)
做齿轮和轴承的设计,齿面的接触疲劳强度一般为1500Mpa,但对于极限工况下可以适当放宽,而轴承滚道的极限强度可4000Mpa。
次表面应力分析
赫兹接触分析仅适用于垂直于表面集中力所引起的表面应力,试验数据表面很多表面的疲劳失效更多的源于次表面,尤其时轴承。
在Baffalo中Sub_Surface_Stress模块中提供了次表面计算的弹性力学方法。
正交剪应力
在滚子滚过滚道时,滚道次表面会产生正交剪应力,每个滚子滚过滚道的应力差值为:
$$
\Delta \tau=2\tau_{yz}
$$
那么轴承的疲劳强度应与剪应力差值成正比,又由于剪应力与接触正压力成正比。所以后续的轴承寿命理论均基于此修正。
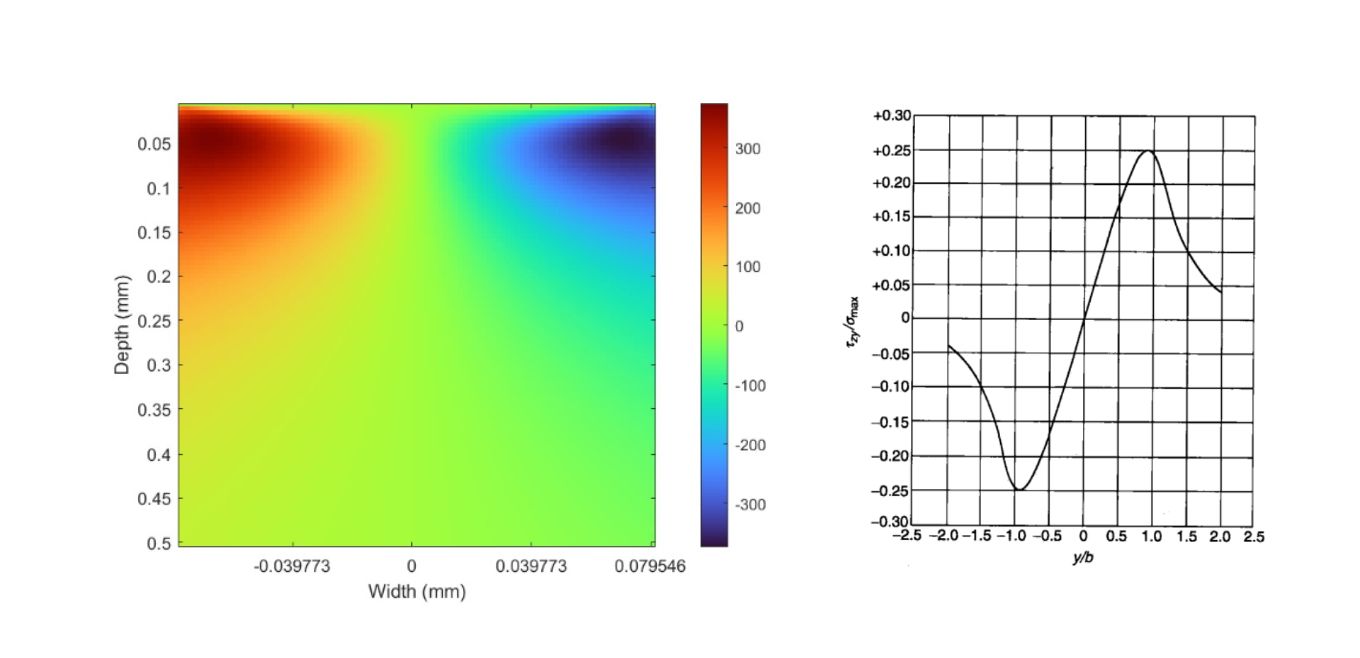
一些教材中,写轴承的寿命与次表面的最大剪应力成正比,最大剪应力与正交剪应力的方向不同,其与表面成45°,笔者更倾向于正交剪应力,因为轴承疲劳失效更多的表现为表面的麻点和剥落,初始裂纹的方向更近似于正交剪应力方向。

主剪应力
次表面主剪应力与接触面呈45°,也称最大剪应力,在齿轮设计中,有种不常见的失效形式与其相关,通常表现为其有一条沿主剪应力方向的主裂纹,失效时随着裂纹的发展会产生另一条伴生裂纹。
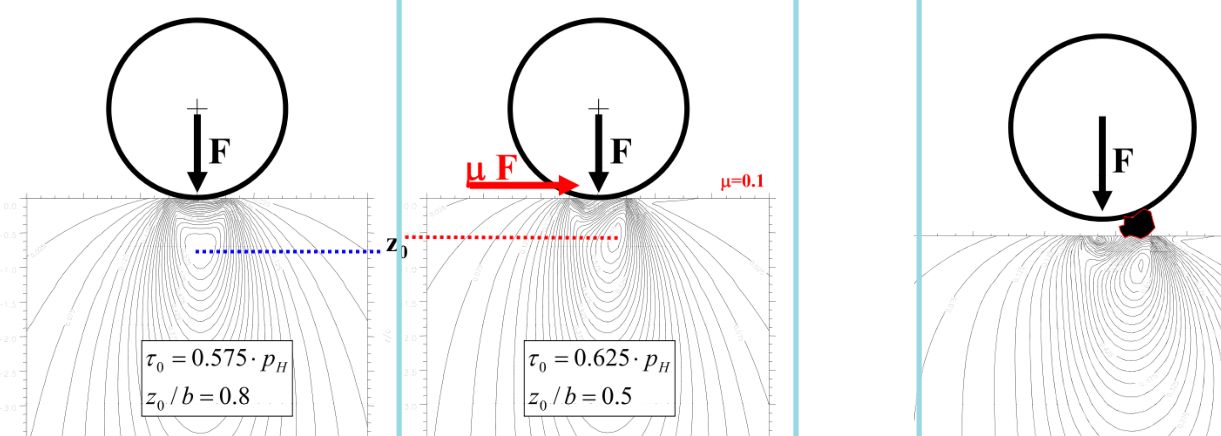
摩擦力影响
通常情况下,齿轮次表面主剪应力的影响并不显著,但当润滑油中有很多碎屑,或者考虑油膜厚度时,次表面的主剪应力显著增大,可等效于接触表面增加了摩擦力。
在Baffalo中通过设置摩擦系数,可进一步分析其影响,加入摩擦力后,次表面的剪应力会有个突起,表现为剪力增大。
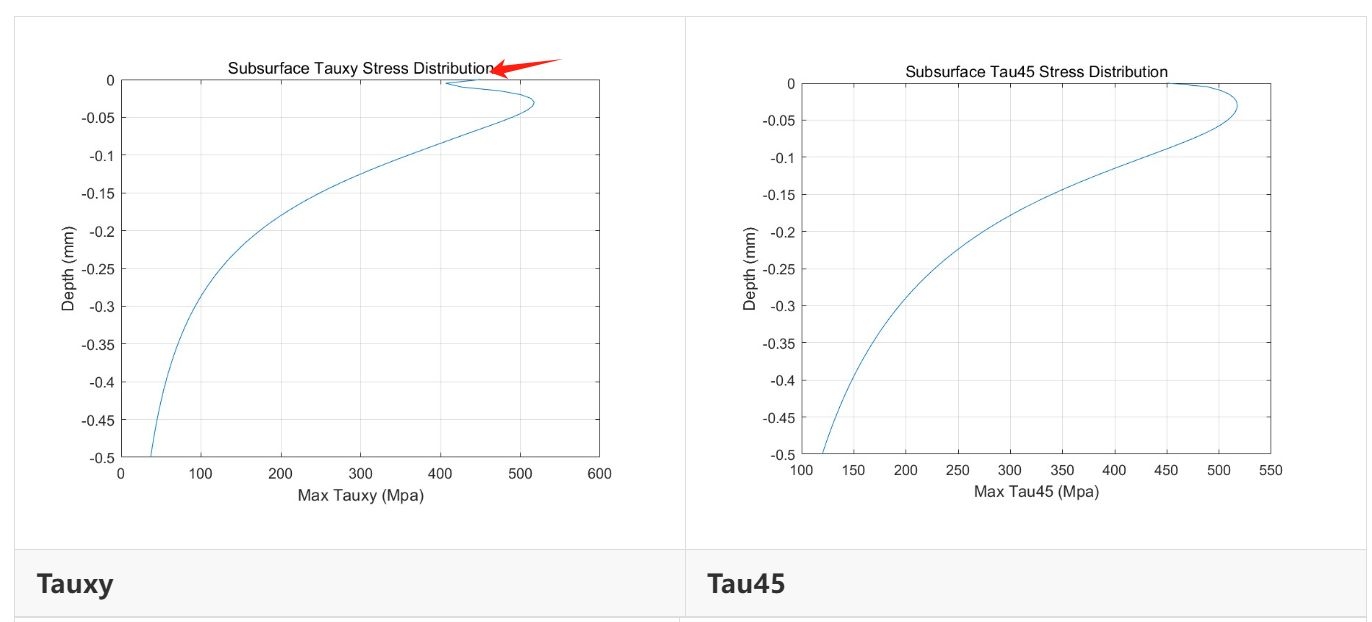
正交剪应力的分布也不像之前那么对称。
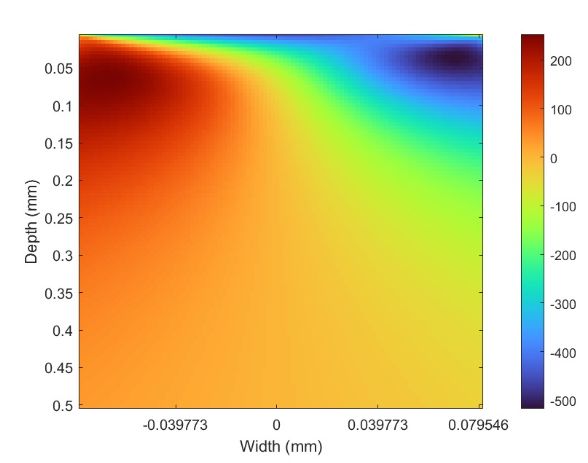
同样在轴承设计领域中,也越来越关注摩擦力的效应,在修正的疲劳寿命中引入清洁度的概念,更加关注润滑油脂对轴承影响。
参考文献
[1] 弹性力学手册
[2] https://www.feacat.com/2025/07/14/HertzContact/
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com