介绍
Ramberg_Osgood用来生成应力应变曲线。
原理
MMPDS $^{[1] [2]}$是美国航空专业最权威的材料标准,包含航空航天领域各种金属材料力学性能。在本规范中,单参数Ramberg-Osgood Parameter n和双参数Dual Bron Parameters n1, n2应力应变曲线被应用来求解金属材料的力学性能。这两种半经验公式可以用来评估材料的强度。
已知材料的弹性模量E, 抗拉强度Ftu, 屈服强度Fty, 断裂伸长率εmax, 通过这几个参数即可求出材料的应力应变曲线。
首先通过极限的抗拉强度和断裂伸长率求出极限应变值$\epsilon_{us}$:
$$
\epsilon_{us}=100(\epsilon_{max}-\frac{F_{tu}}{E})
$$
接着应用极限应变值,求出Ramberg-Osgood系数n:
$$
n=\frac{ln(\epsilon_{us}/0.2)}{F_{tu}/F_{ty}}
$$
运用Hill $^{[46]}$提出的方程算出材料的应力应变曲线:
$$
\epsilon=\frac{\sigma}{E}+0.002(\frac{\sigma}{F_{ty}})^n
$$
材料的真实应力和应变值和工程应力应变为log关系,由下式可得:
$$
\epsilon_{true}=ln(1+\epsilon)
$$
$$
\sigma_{true}=\sigma(1+\epsilon)
$$
类结构
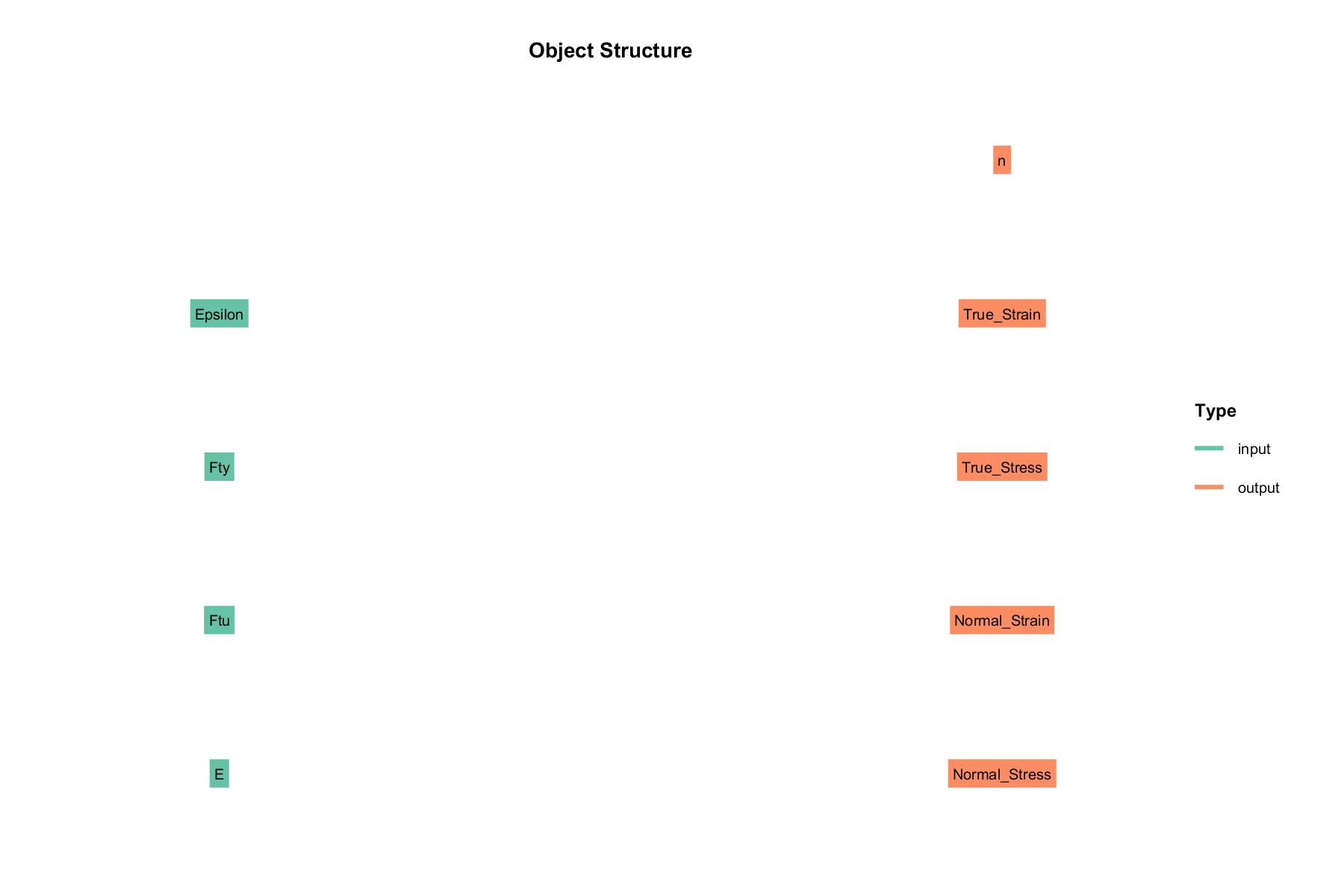
输入 input:
- Fty : 材料屈服强度
- Ftu : 材料拉伸强度
- E : 弹性模量
- Epsilon : 断裂延伸率
输出 output :
- n : 参数
- True_Strain : 真实应变
- True_Stress : 真实应力
- Normal_Strain : 名义应变
- Normal_Stress : 名义应力
案例
inputStruct1.E=71018.5;
inputStruct1.Ftu=468.8;
inputStruct1.Fty=386.12;
inputStruct1.Epsilon=0.1;
paramsStruct1=struct();
obj1=method.Stress_Strain_Curve.Ramberg_Osgood(paramsStruct1,inputStruct1);
obj1=obj1.solve();
obj1=obj1.plot();
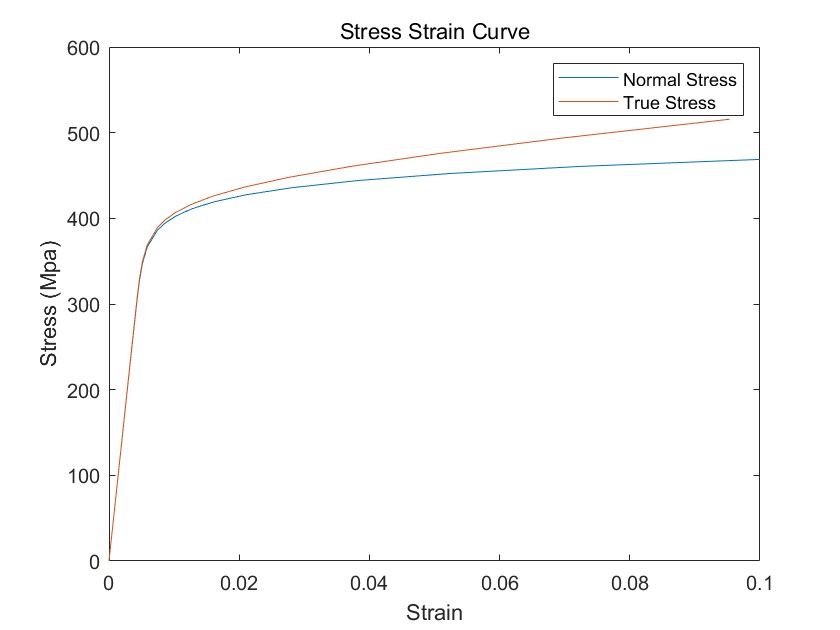
参考文献
[1] DOTFAAAR-MMPDS-01_Metallic Materials Properties Development and Standardization(MMPDS)
[2] Metallic Materials Properties Development and Standardization (MMPDS-11)
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com