齿轮的网格通常要求采用映射的方式画网格,在齿廓和齿根圆弧要有明显的边界,这个边界点为齿廓的起点,也是接触的起点。这样的分界好处时后期做齿廓修形时可以很方便的修改齿形,而齿根的圆弧与刀具的选择相关性很大,做齿根圆弧优化时也可以只调整齿根曲线。
另外在做接触或者接触斑的分析时,齿廓一般不用考虑侧隙,这样就不用花费额外时间调整齿形副的装配位置,以便更好的帮助分析收敛,所以再用Kisssoft或者Romax导出齿形时,建议将侧隙调整为0。
齿廓的曲线方程
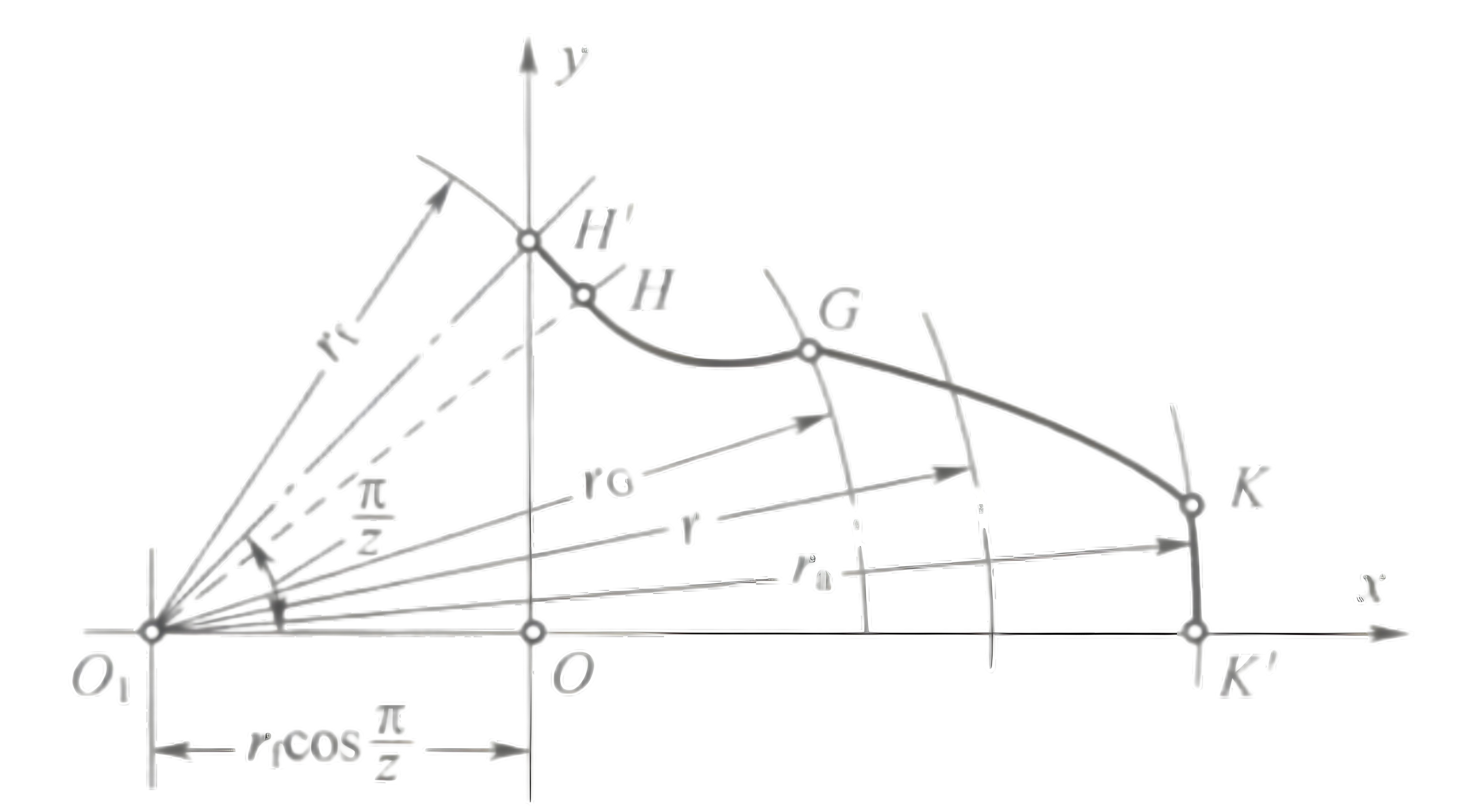
在齿轮计算中有很多公式,但实际只要掌握了齿廓曲线,其他的几何参数都可以直接通过齿形分析得到。以下内容摘自于参考文献[1],下图是一个无修缘无根切齿轮的端面齿廓。由下列四段曲线构成:
齿根圆弧HH’,半径等于$r_f$;
过渡曲线HG;
基本齿廓曲线KG:
齿顶圆弧KK’,其半径为r_a。
齿顶圆系制作齿坏时车制而成,而齿根圆是滚刀节线在齿轮分度圆上滚动时,由顶刃包络切成。按下图中所示配置齿轮坐标系Oxy,其中Ox轴是齿廓的对称轴,与0x轴相垂直的Oy轴通过齿根圆与齿槽对称轴的交点H,于是便确定了坐标原点O,它与齿轮轴心O之间的距离为 $r_fcos(\pi/z)$。
下图(a)所示为用一齿条刀加工齿轮的示意图,坐标系$Px_0y_0$固连于刀具之上,其坐标原点为节点P,刀具中线与节线之距离为xm(变位量)。
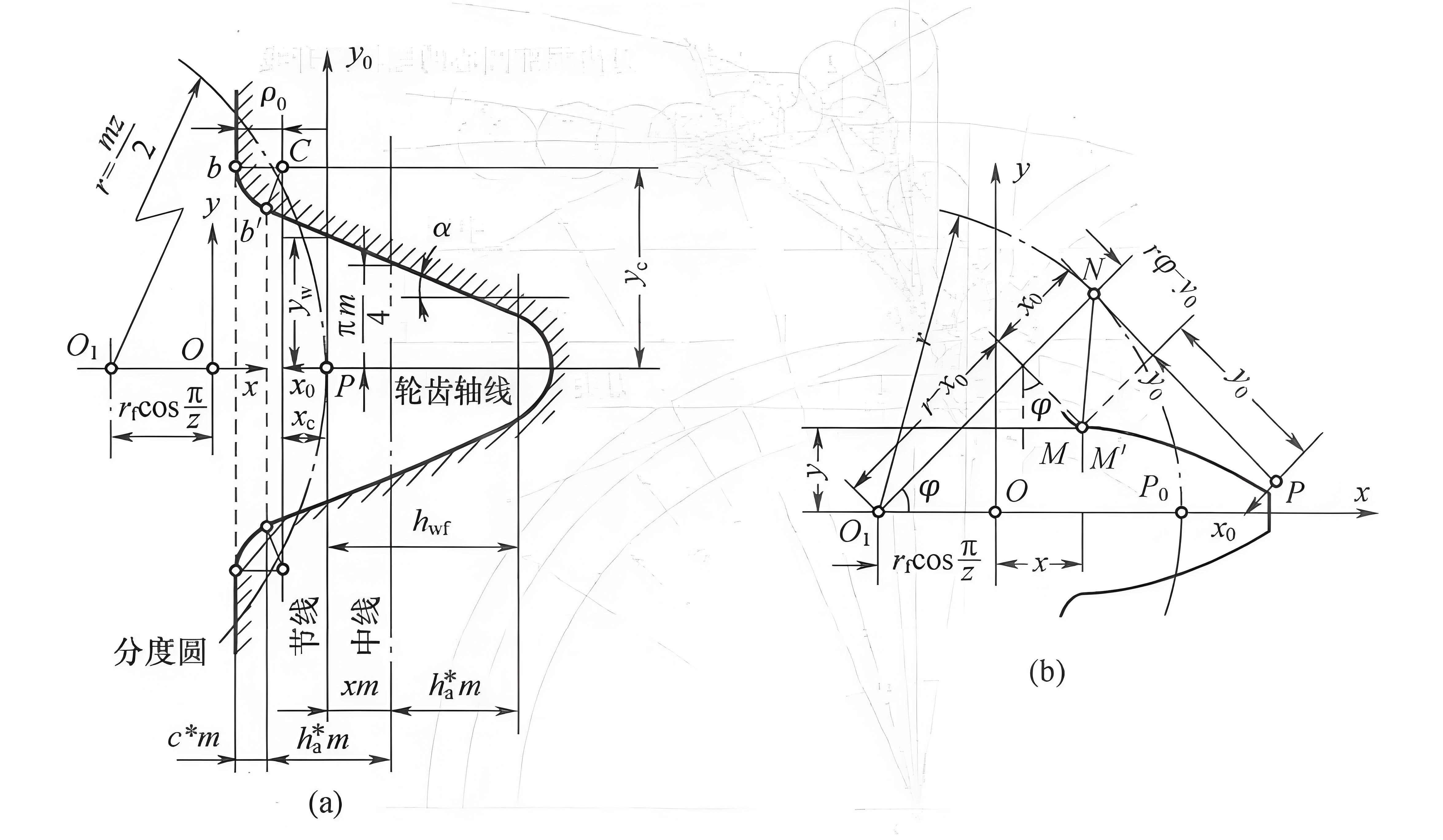
设刀具齿廓上任意一点M’在刀具坐标系$Px_1y_1$中的坐标为x0和y0,该点的法线M’N与刀具节线$Py_0$的交点为N;在刀具节线沿齿轮分度圆滚动的过程中,当N点与分度圆接触时,点 M将与齿轮齿廓上的对应点M接触(如上图(b)所示),二者的公法线亦通过N点。于是,把M’点在坐标系$Px_0y_0$中的坐标xo、yo转换至坐标系Oxy中,即可得到齿轮齿廓上相应M 点的坐标x、y。设齿条刀滚动角为Φ,则:
$$
x=(r-x_0)cos\phi+(r_{\phi}-y_0)sin\phi-r_fcos(\frac{\pi}{z})
$$
$$
y=(r-x_0)sin\phi-(r_{\phi}-y_0)cos\phi
$$
$$
\phi=\frac{\overline{PN}}{r}
$$
上式即是用齿条刀加工的齿轮齿廓普遍方程式,也是x0、y0和\phi的函数。因此,若已知刀具齿廓上任意点M’的坐标(x0、y0)、$\overline{PN}$及r的值时,就可以用上式求出该点(齿轮齿廓上相应点为M)在齿轮坐标系Oxy中的坐标(x、y)。若取齿条刀具上的若干点,利用上式求出齿轮齿廓上相应各点的坐标(x、y)加以连结,便得到所加工齿轮的齿廓曲线。顺便指出,用齿轮滚刀切制齿轮时,也近似地将其当作用齿条刀加工,故研究结果也适用于滚齿。
齿轮齿根过渡曲线HG段是由齿条刀的齿顶倒圆部分bb’所切出的(如下图所示)。M’在刀具坐标系$Px_0y_0$中的坐标(x0,y0)为:
$$
x_0=x_c+\rho_0cos\gamma
$$
$$
y_0=y_c-\rho_0sin\gamma
$$
$$
\gamma=arctan\frac{r\phi-y_c}{x_c}
$$
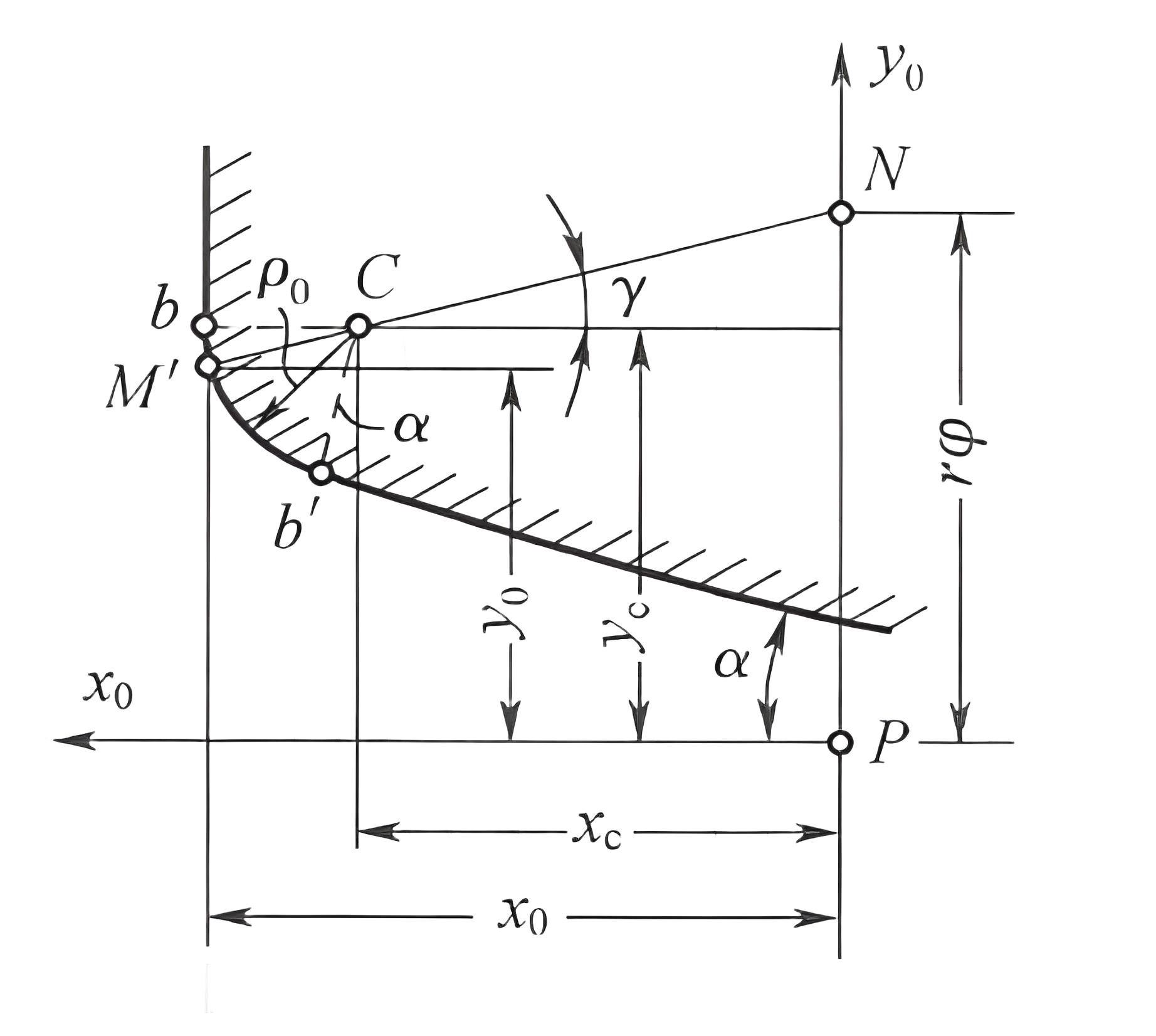
式中角度$\gamma$在下述范围中变动:
$$
0\le\gamma\le(\pi/2-\alpha)
$$
式中。$\alpha$为齿条到的齿形角,一般为20°。
将(4)(6)式带入 (1)(3)式可以得到齿轮齿廓齿根的过渡曲线方程:
$$
x=(r-x_c-\rho_0cos\gamma)cos\phi+(x_ctan\gamma+\rho_0sin\gamma)sin\phi-r_fcos(\frac{\pi}{2})
$$
$$
y=(r-x_c-\rho_0cos\gamma)sin\phi+(x_ctan\gamma+\rho_0sin\gamma)cos\phi
$$
建模
在Baffalo中的SingleGear模块可以直接生成单个齿轮。
inputSingleGear.mn= 1;
inputSingleGear.alphan = 20;
inputSingleGear.Z=17;
inputSingleGear.b=10;
inputSingleGear.x=0.3;
inputSingleGear.beta=20;
paramsingleGear.MeshNTooth = 17;
obj1=gear.SingleGear(paramsingleGear, inputSingleGear);
obj1=obj1.solve();
PlotCutting(obj1);
PlotToolCurve(obj1);
PlotGearCurve(obj1);
Plot2D(obj1);
Plot3D(obj1,'faceno',101);
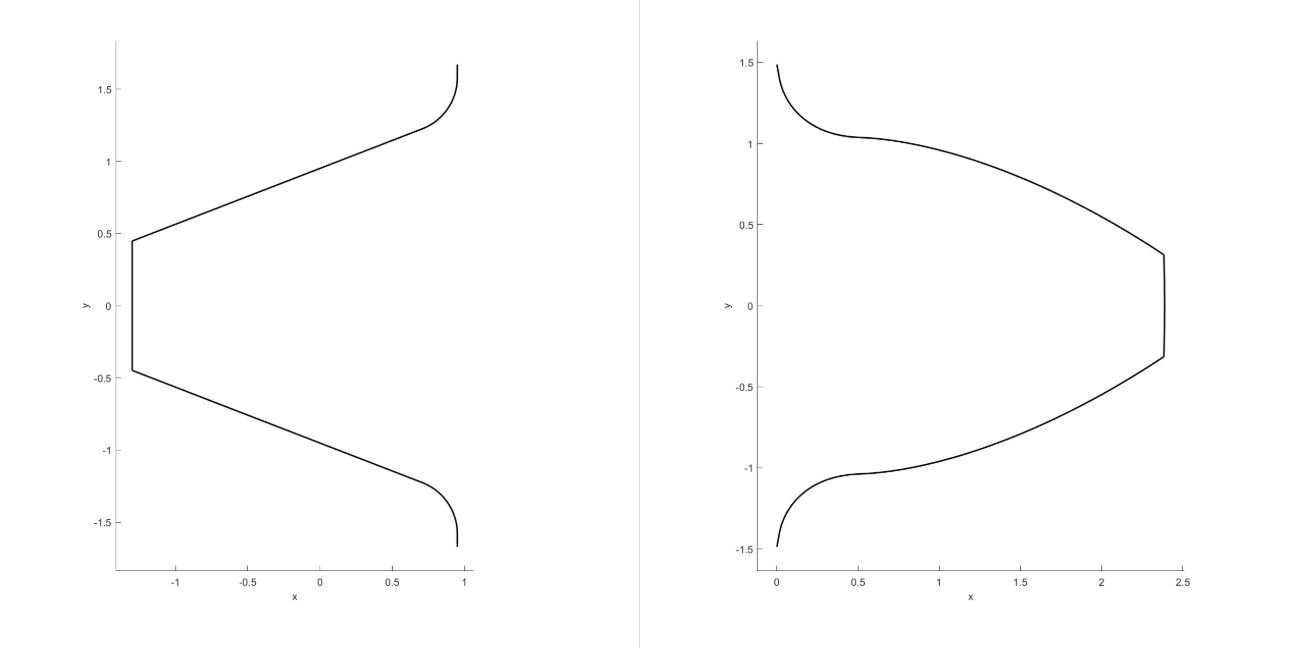
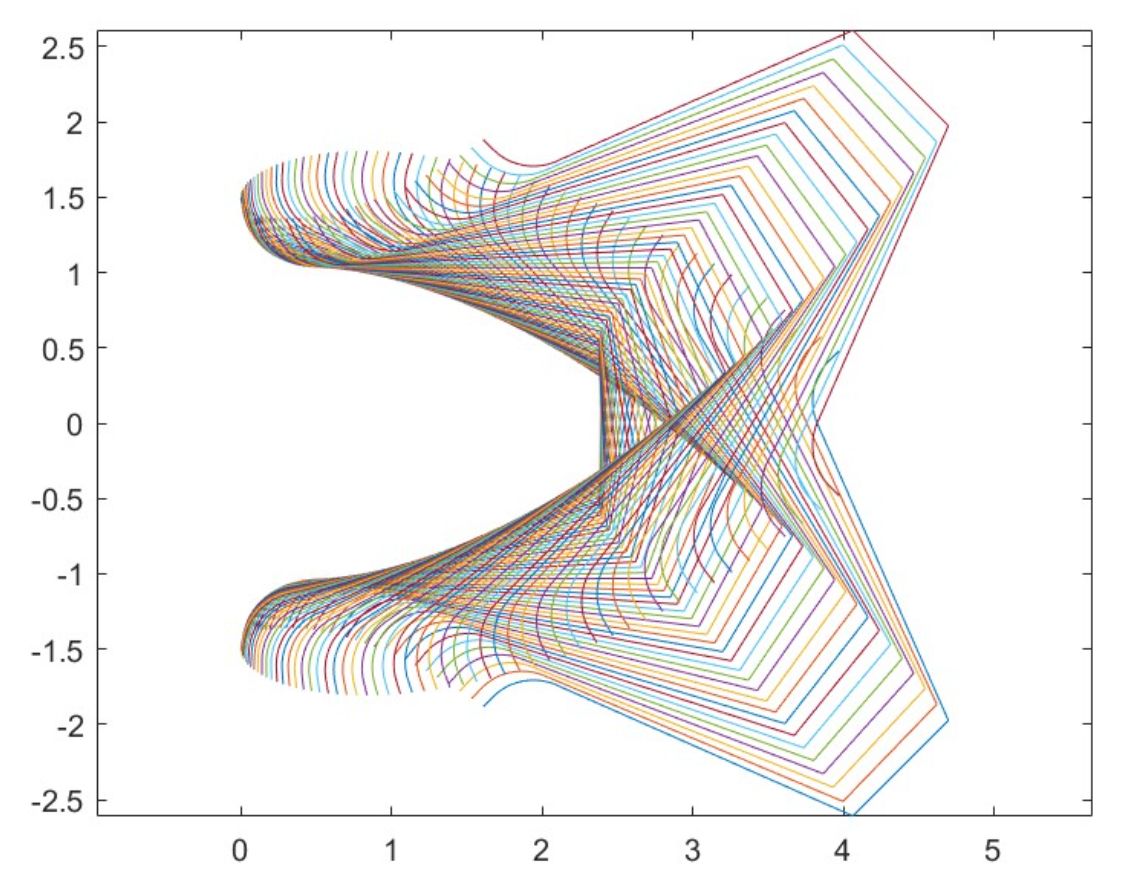
刀具和单个齿形绘制:
建立的实体网格如下,同时齿面也做了编号处理,方便后期提取数据。
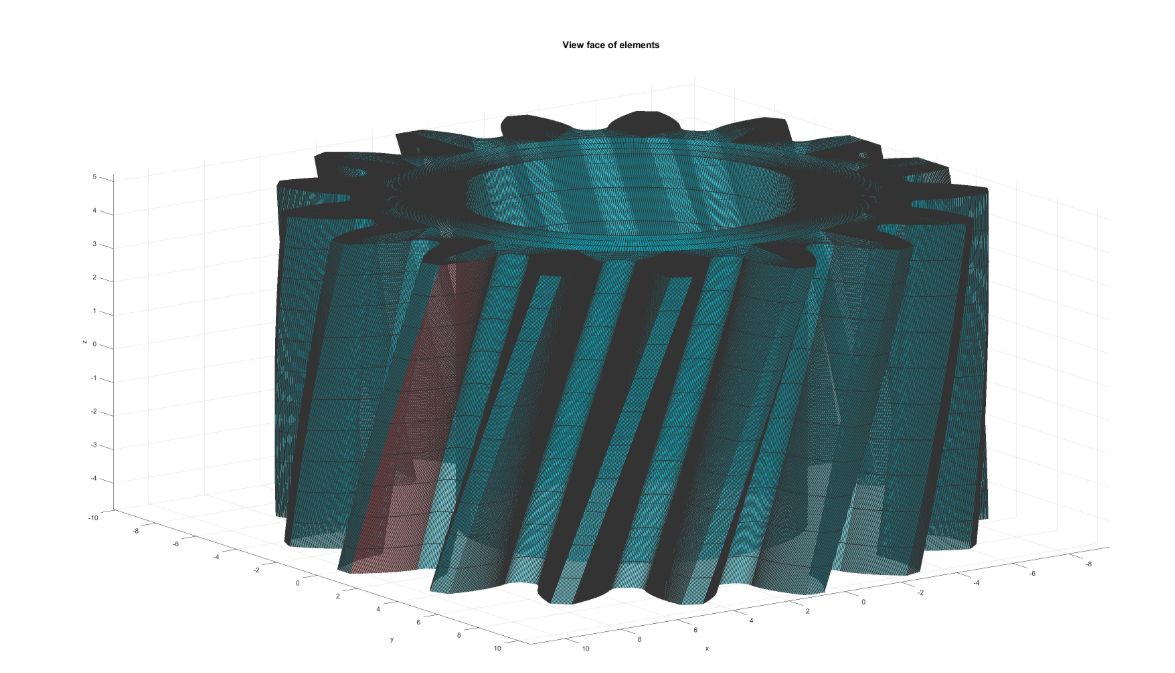
参考文献
[1] 圆柱齿轮几何计算原理及实用算法
[2] https://www.feacat.com/2025/07/22/SingleGear/
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com