介绍
赫兹接触解释了无限长圆柱体的接触问题,无限长柱体之间的理想线接触状态在实际问题中是不存在的。在滚子轴承中,滚子的长度一般都小于滚道的宽度,而当滚子的轮廓不是一条直线,并且滚子相对于滚道产生倾斜时,这样的问题无法用Hertz 线接触理论解决,此类问题被称为非Hertz问题。
非赫兹接触
首先观察赫兹接触条件下的压力分布,其截面的压力为:
$$
p(x)=p_{max}\sqrt{1-(x/b)^2}
$$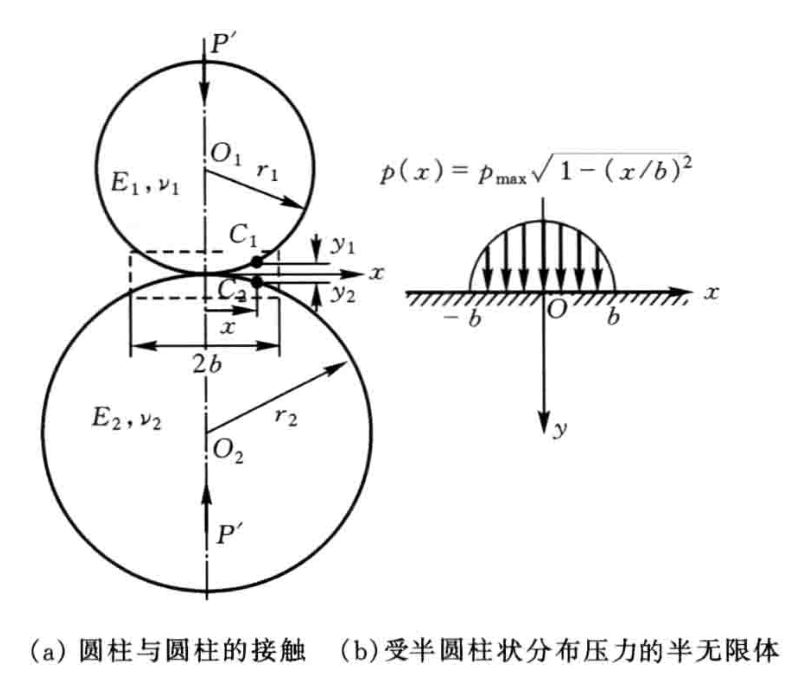
对于有限长的滚子,我们不妨假设沿滚子素线方向将可能接触区域划分为n个条形单元,在单元内假定接触应力沿素线方向(y轴)为均匀分布,沿横向(r轴)按Hertz分布,如下图所示: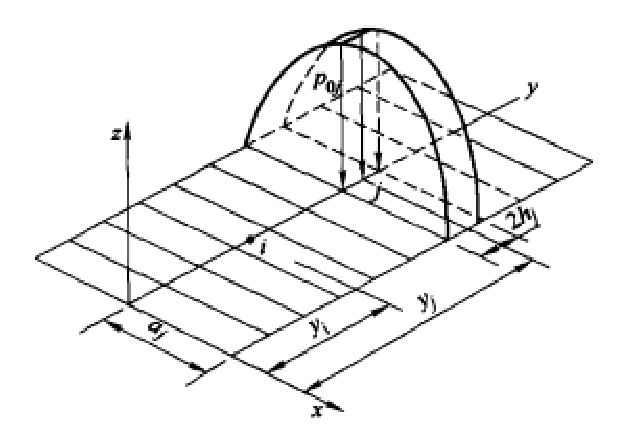
我们将其类比于一个结构力学问题F=kx,一个截面相当于一个梁,那么要求解这个整体的变形和受力,最关键的是需要求解整个结构的刚度矩阵:
$$
k=\begin{bmatrix}
k11 & k12 & k12 \
k21 & k22 & k23 \
k31 & k32 & k33
\end{bmatrix}
$$
通过力学分析和数值计算可以得到改矩阵,在 滚动轴承分析计算与应用[2]一书中介绍了该方法,感兴趣的读者可以参阅该书。最终要得到滚子接触斑应力的分布,可通过这种切片的思想再引入牛顿迭代法求得: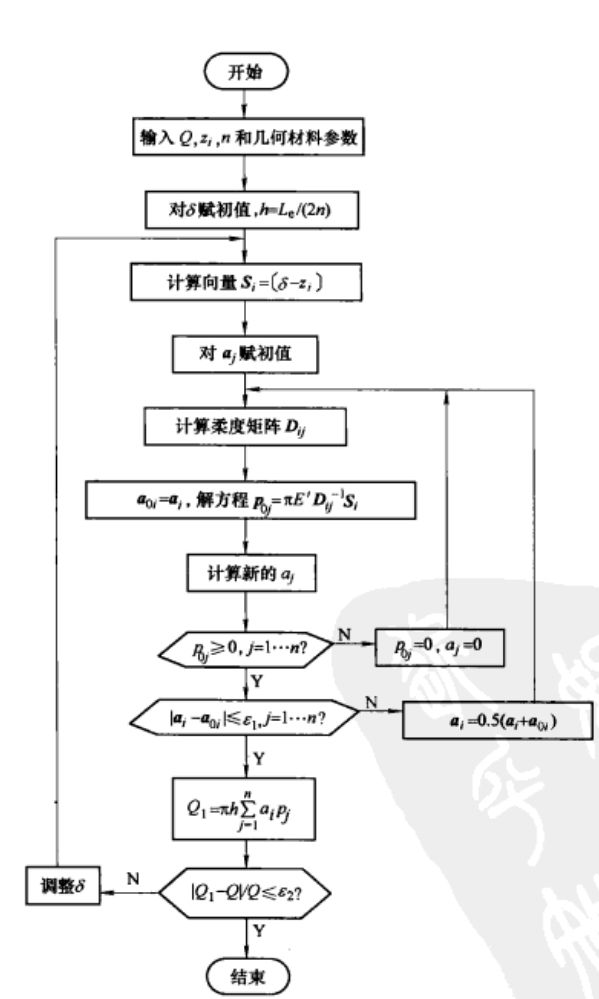
滚子修形
目前这种切片的非赫兹接触分析的方式已集成在Romax和一些轴承供应商的专用分析工具中, 在Baffalo中可方便分析滚子修形的影响。
修形对比
本案例选自 滚动轴承分析计算与应用[2],圆柱滚子与半空间表面接触。滚子素线中部为直线,两端圆弧修型,如下图所示。已知D=10mm,L=14mm,r=0.7mm,L=9mm, R。=1800mm,首先按照Q=920N施加外载荷。
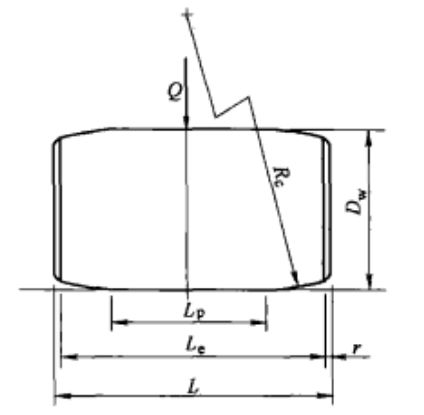
两端圆弧修形的公式如下:
当 $|y| \le L_p/2$
$$
Z(y)=(L_p/2+y)
$$
当 $|y| \gt L_p/2$
$$
Z(y)=(L_p/2+y)+\frac{y^2-(L_p/2)^2}{2R_c}
$$
无修形滚子接触应力,可以看到两端的应力集中非常严重:

圆弧修形滚子接触应力,虽然改善了两端的应力集中,但由于曲率不连续,仍然有应力集中现象:

倾角分析
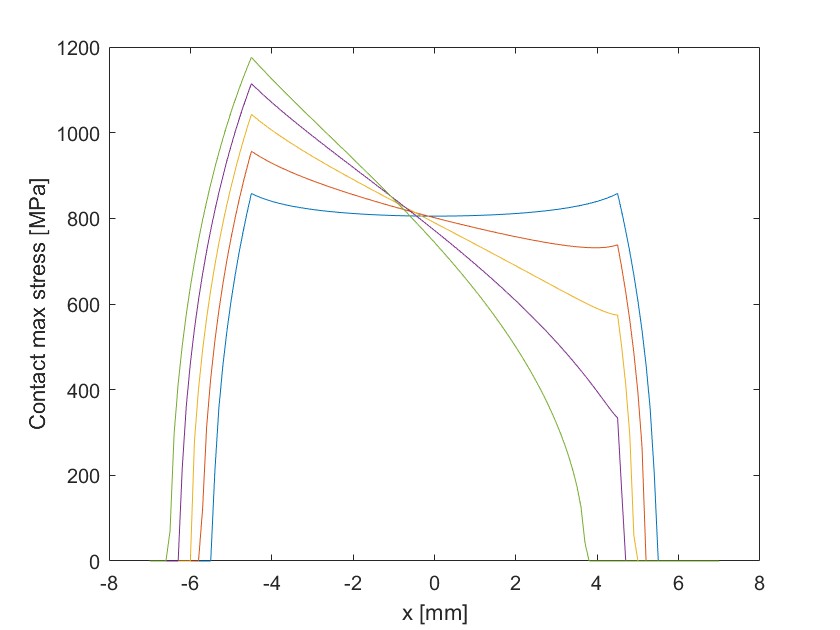
考虑滚子倾角对接触应力的影响,倾角的角度为 0.0086~0.043°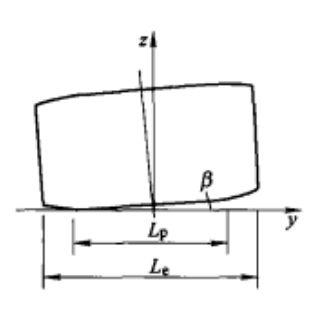
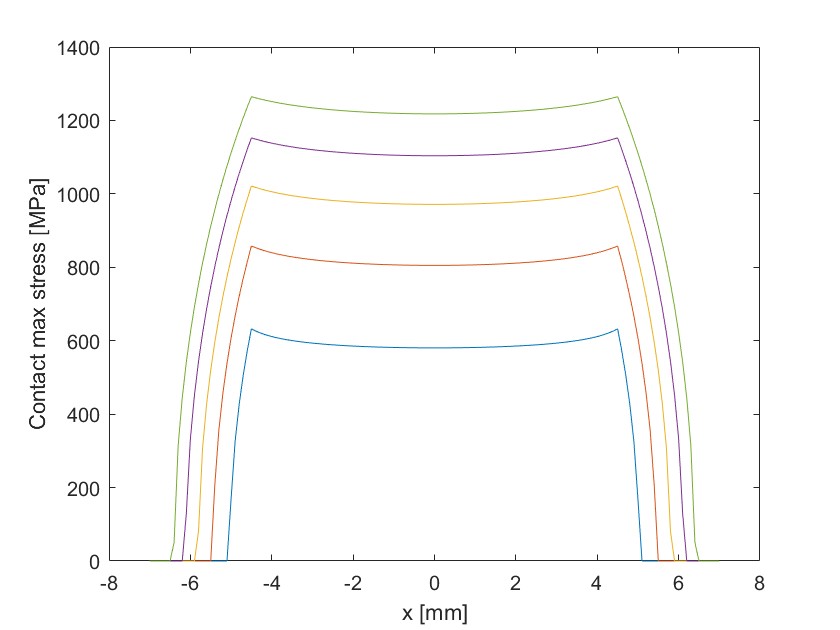
外载荷分析
设置倾角为0,载荷由460~2300变化,得到的最大接触应力图:
参考文献
[1] https://www.feacat.com/2025/07/15/%E8%B5%AB%E5%85%B9%E6%8E%A5%E8%A7%A6%E5%92%8C%E6%AC%A1%E8%A1%A8%E9%9D%A2%E5%BA%94%E5%8A%9B%E5%88%86%E6%9E%90/
[2] 滚动轴承分析计算与应用
[3] 弹性力学手册
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com