介绍
1934年举行的国际国家标准化协会(ISA)会议上首次讨论了滚动轴承负载等级的计算方法,自此开启了滚动轴承标准化计算的序列。
1945年的ISA会议上,滚动轴承寿命计算方法首次得到提议。自1947年和1952年 Lundberg与 Palmgren 提出基于次表面应力的寿命预测模型 以来,该理论方法得到广泛的认可。
1962年,第一套规范化的轴承寿命建议计算方法 ISO/R 281发布。

1977年,ISO 281-1:1977 规范中引入了可靠度的概念,进一步完善了规范。
ISO 281: 1990
1990年,ISO 281-1:1977 被 ISO 281:1990取代,自此轴承寿命的计算方法已基本稳定,后续规范都基于此做不同的修正。
基本额定寿命
深沟球轴承的基本额定寿命可由下式计算:
$$
L_{10}=(\frac{C_r}{P_r})^3
$$
$C_r$为基本额定动载荷,$P_r$为当量动载荷。下标10的表示可靠度为90%。上标3为寿命系数,与接触的类型相关,一般点接触的寿命系数为3,线接触的寿命系数接近4,而滚子轴承的接触形式介于点接触和线接触之间,ISO规范取为10/3。
$P_r$为当量动载荷,需根据实际工况换算。$C_r$为额定动载荷,这个系数各个供应商的轴承手册都有说明,当轴承选定,该系数就已经敲定了。
我们主要关注下轴承寿命的修正公式,ISO 281:1990中对于寿命的修正如下:
$$
L_{na}=a_1a_2a_3L_{10}
$$
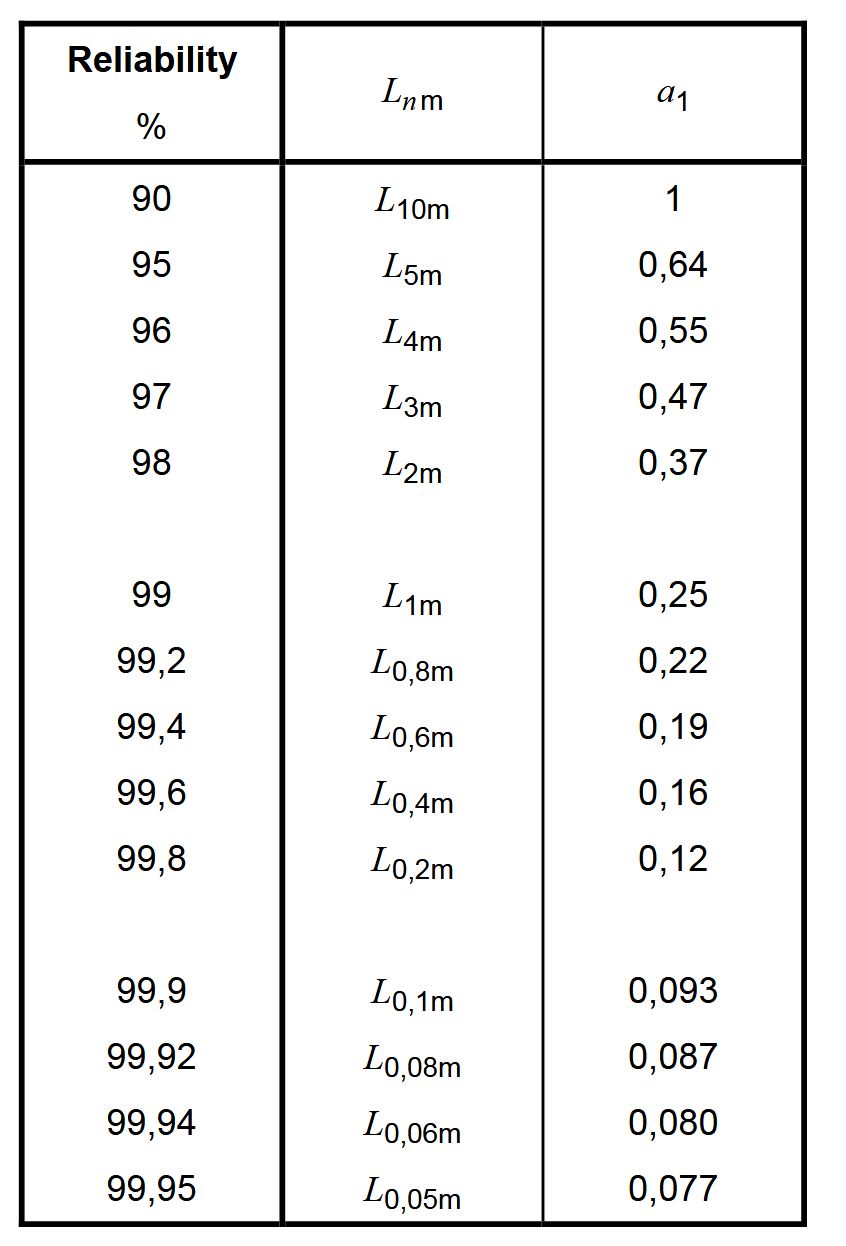
系数$a_1$是可靠度的修正系数,基于威布尔分布,可由下表查询。
系数$a_2$是一个工艺参数,可以理解为某个轴承用来某种工艺,或者某种新材料,这部分提升可用$a_2$表示,因此$a_2$是一个经验参数,并没有具体可参照的数值。
系数$a_3$是工况修正系数,比如说我的轴承将要运行在少油的环境中,因为得不到充分的润滑,寿命有所降低,此时可用$a_3$修正。$a_3$也是个经验系数。
可以看出来,ISO 281:1990规范给了轴承基本额定寿命,但对于轴承工艺和材料的提升,以及具体轴承使用工况并没有很多经验。
ISO 281 : 2007
ISO 281:2007 对于轴承基本额定寿命的做了更细致的修正:
$$
L_{nm}=a_1a_{ISO}L_{10}
$$
式中,$a_1$为可靠度的修正。$a_{ISO}$ 为系统的修正系数,其更加侧重于使用场景的修正。ISO 281: 1990对工艺和材料的修正系数 $a_2$ 并入了基本额定寿命的修正中。
对于深沟球轴承,$a_{ISO}$ 可由下式计算:
$$
a_{ISO}=0.1(1-(2.5671-\frac{A}{k^B})^{0.83}(\frac{e_cC_u}{P}))^{-9.3}
$$
式中,k为运动粘度比例,A和B是于运动粘度相关的常数,$e_c$与润滑油中的颗粒相关,$C_u$ 是一个与疲劳相关的系数。
ISO 281:2007对于轴承使用场景,尤其是润滑这有了更深刻的理解和认识。但对于轴承和材料和工艺相关的系数,基本毫无建树,这很大程度上归功于整个轴承行业的垄断。
ISO/TS 16281
ISO /TS 16281 规范在轴承的使用场景上发力,对于球轴承,进一步考虑了游隙和倾斜的影响,明确了滚子的刚度。在滚子轴承中,引入了滚子切片的影响。
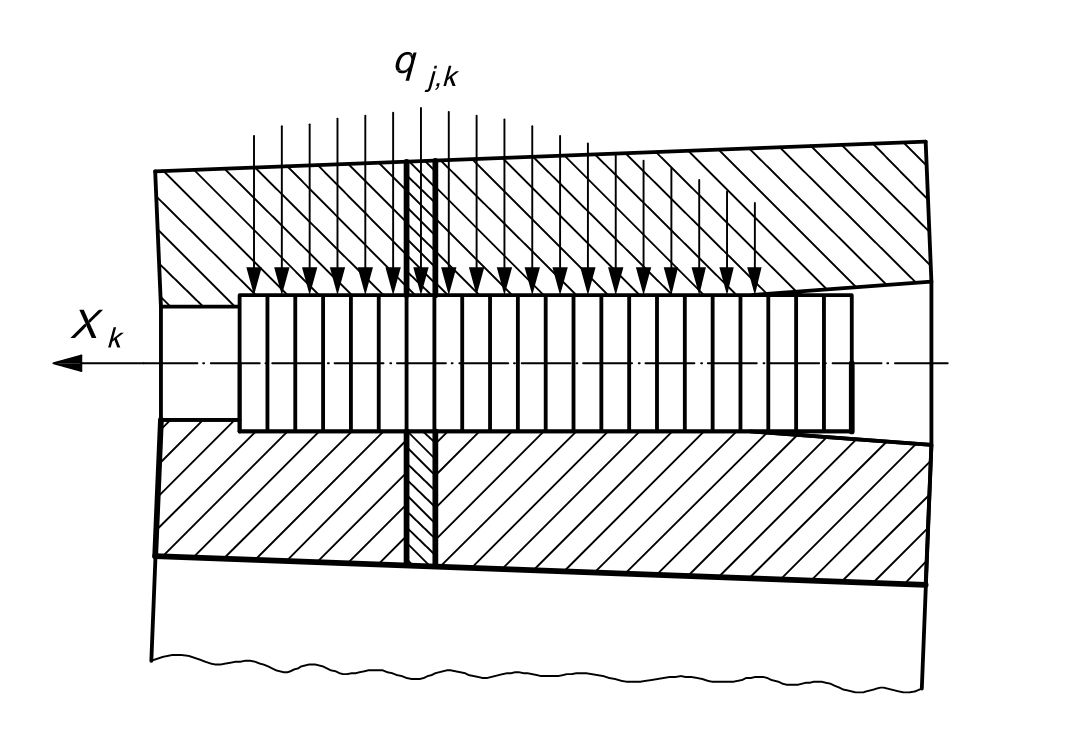
从某种程度上讲,这份规范对于现代轴承轴承分析影响深远,它不再视轴承为一个整体。而是将其分开为内圈、外圈和滚子,定义了滚子刚度,使得一些加工的几何误差和游隙的分析成为可能。比如内外圈的椭圆度,我可以调整滚子的刚度,来分析具体滚子的受力。
美中不足的是,这份规范虽然将轴承受力拆分为滚子受力,但其并没有将轴承的寿命进一步拆分到滚子层级。
在后续的文章中,我将一步细分轴承寿命,引入滚子滚道的寿命计算,将轴承寿命与SN曲线挂钩。
参考文献
[1] ISO 281
[2] ISO/TS 16281
[3] Evolution of rolling bearing life rating through the standardization
[4] ISO/R 281
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com