介绍
在之前的文章中介绍了非赫兹接触滚子修形分析方法[1], 大量的研究表明,直线型轴承滚子两端存在着严重的应力集中,可以高达中部应力的3~7倍,如下图所示。边缘应力集中导致早期疲劳剥落,降低了滚子轴承的承载能力。
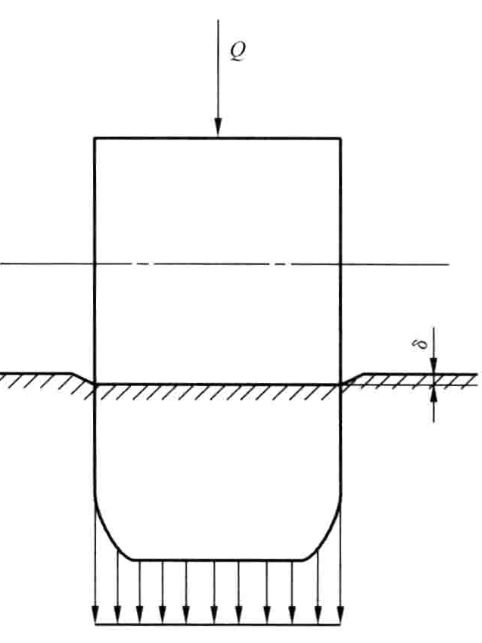
本文简单介绍不同滚子母线修形方法下的母线方程。
滚子修形
对数修形
一般在分析软件中包括Kisssoft和Romax在默认条件下都为对数修形,对于常规的钢滚子,其对数修形方程如下:
如果滚子长度小于2.5倍的滚子直径$L_{we} \le 2.5 D_w$:
$$
P(x_k)=0.00035D_wln[\frac{1}{1-(2x_k/L_{we})^2}]
$$
当滚子长度大于2.5的滚子直径时$L_{we}>2.5D_w$时:
当$|{x_k}| \le \frac{L_{we}-2.5D_{we}}{2}$,$P(x_k)=0$
当$|{x_k}| \gt \frac{L_{we}-2.5D_{we}}{2}$,
$$
P(x_k)=0.00050D_wln(\frac{1}{1-[[2|x_k|-(L_{we}-2.5D_{we})]/2.5D_{we}]^2}
$$
弧坡修形,圆心在中线上
弧坡修形取滚子单面的凸度约等于滚子与滚道之间的变形量:
$$
\Delta c=\delta
$$
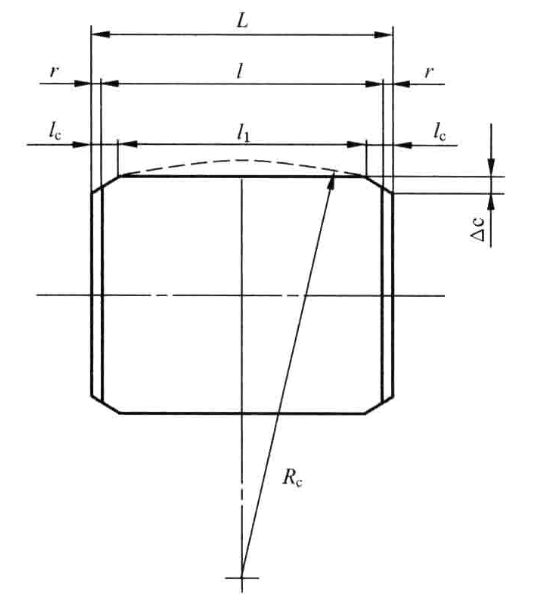
母线边缘的长度为:
$$
L_c=0.15l
$$
圆弧半径近似取:
$$
R_c=\frac{l^2-l_1^2}{8\Delta c}
$$
弧坡修形,圆心在两侧
上节的弧坡修形,由于圆心在中线上,导致中段和边缘曲线是不连续的,为了使得滚子母线更加光滑,可以把圆心调整到两侧。
仍然取母线边缘的长度为:
$$
L_c=0.15l
$$
圆弧半径近似取:
$$
R_c=\frac{l^2}{88\Delta c}
$$
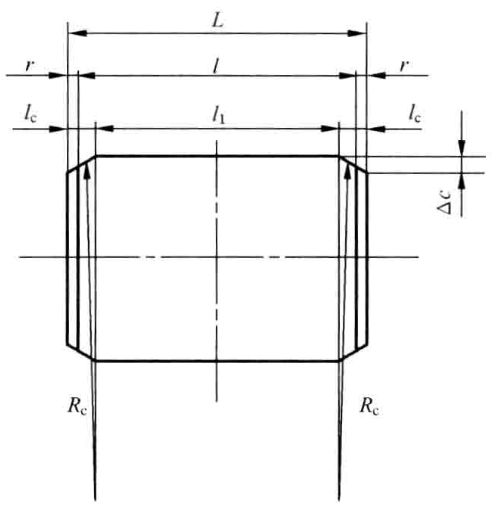
全凸滚子
全凸滚子的型面如同对称球面滚子,只是圆弧半径非常之大。这种修正方法的优点是不仅可以消除或减小边缘效应引起的应力集中,还可以有效地消除或减小轴线偏斜引起的端部应力集中。缺点是实际负荷小于计算负荷时实际接触长度减小,中部应力高,还会降低疲劳寿命。
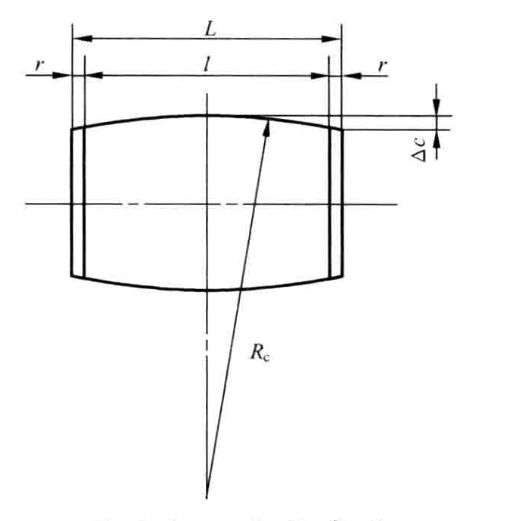
全凸滚子取:
$$
\Delta c=\delta
$$
$$
R_c=\frac{l^2}{8\Delta c}
$$
参考文献
[1] https://www.feacat.com/2025/07/28/%E9%9D%9E%E8%B5%AB%E5%85%B9%E6%8E%A5%E8%A7%A6%E5%92%8C%E8%BD%B4%E6%89%BF%E6%BB%9A%E5%AD%90%E4%BF%AE%E5%BD%A2/
[2] 滚动轴承设计原理
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com