介绍
滚动轴承作为机械系统中的关键部件,具有非线性的特性,对计算方法要求很高。在之前的文章中介绍了如何建立滚子轴承,本文以深沟球轴承为例,介绍球轴承的有限元建模分析方法。
球轴承
几何关系
尽管滚珠轴承看似是简单的机械元件,但其内部几何结构,以及相应的运动和应力关系却相当复杂。最重要的几何参数如下图所示,该图展示了深沟球轴承(在径向载荷作用下)的变形。其中两个参数是滚珠直径D和节圆直径Dm,滚珠围绕轴承轴线在节圆直径上转动。内圈和外圈的滚道沟曲率半径ri和ro略大于滚珠半径,一方面稍大的曲率半径可以防止轴承卡死,另一方面这些微小的间隙中能贮藏润滑油脂,帮助散热,沟曲率半径率k来表征:
内滚道沟曲率半径ki:
$$
k_i=r_i/D
$$
外滚道沟曲率半径ko:
$$
ko=ro/D
$$
沟曲率半径均要求大于0.5,如果没有实际数据可以取0.52。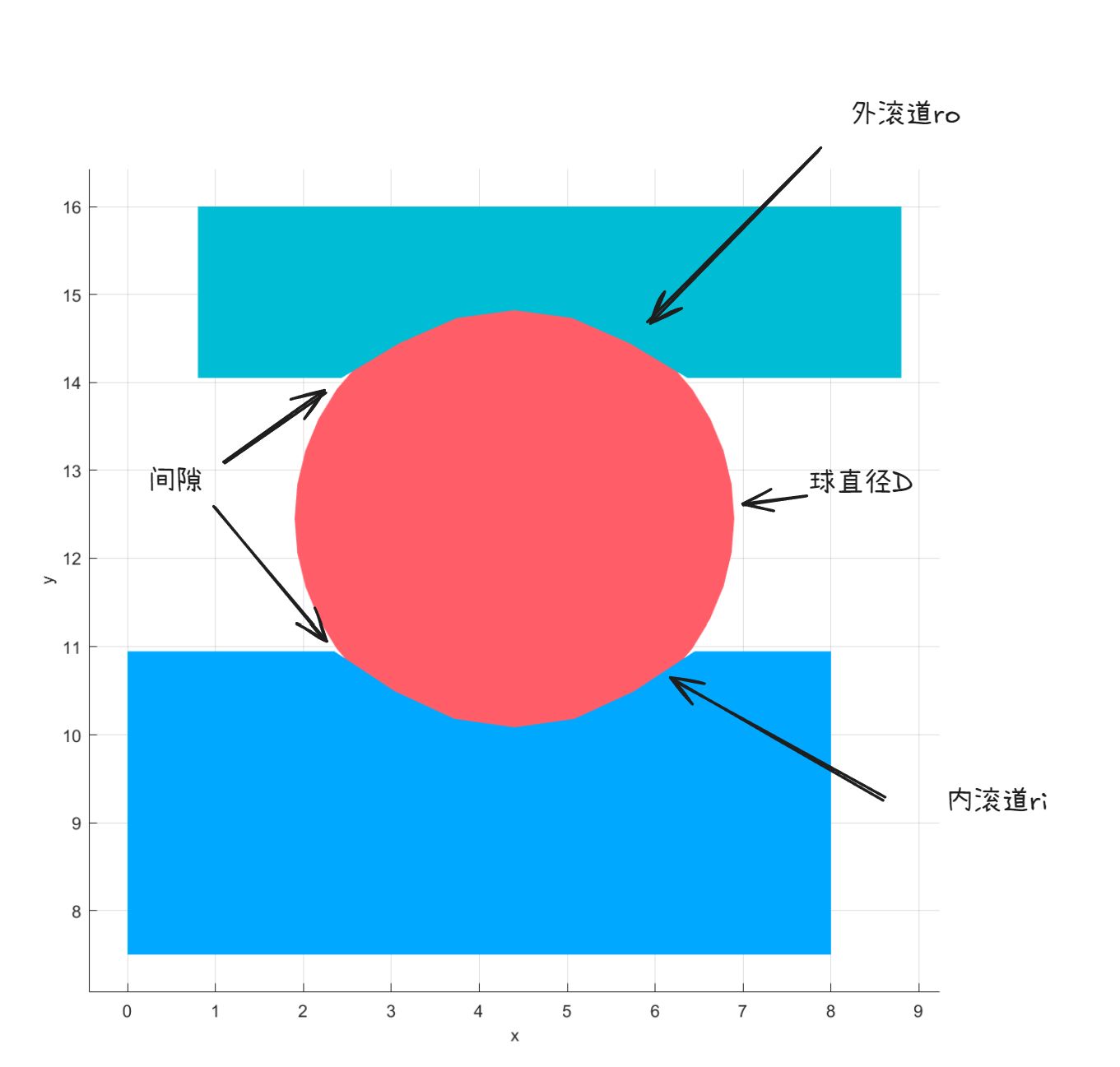
刚度曲线
从几何角度来看,滚珠力的方向可以从轴承套圈相互之间的位置推导得出。确定力的大小则需要用到赫兹点接触理论。对于相互挤压的两个非一致性弹性体的局部应力和变形,赫兹 建立了相关理论。对于钢质物体,两物体在接触点处的相互接近量 δ(单位:毫米)取决于力 F(单位:牛顿):
$$
\delta=2.79e^{-4}\delta^*(\sum \rho F^2)^{1/3}
$$
式中$\delta ^*$为赫兹接触插值参数,$\rho$为曲率
对于不考虑游隙的情况下,滚子的刚度曲线即为点接触的刚度曲线。
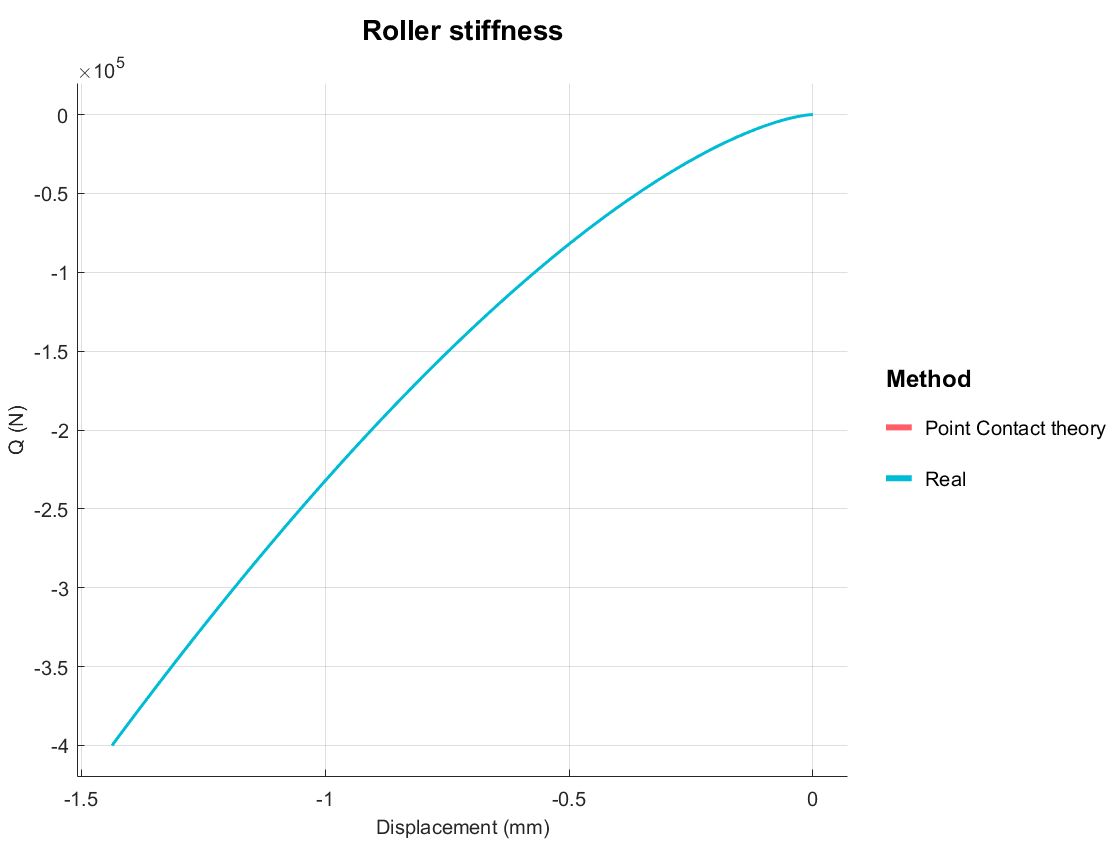
对于该深沟球轴承,在外荷载作用下的滚子受力如下,在径向载荷下有三个滚子受力。
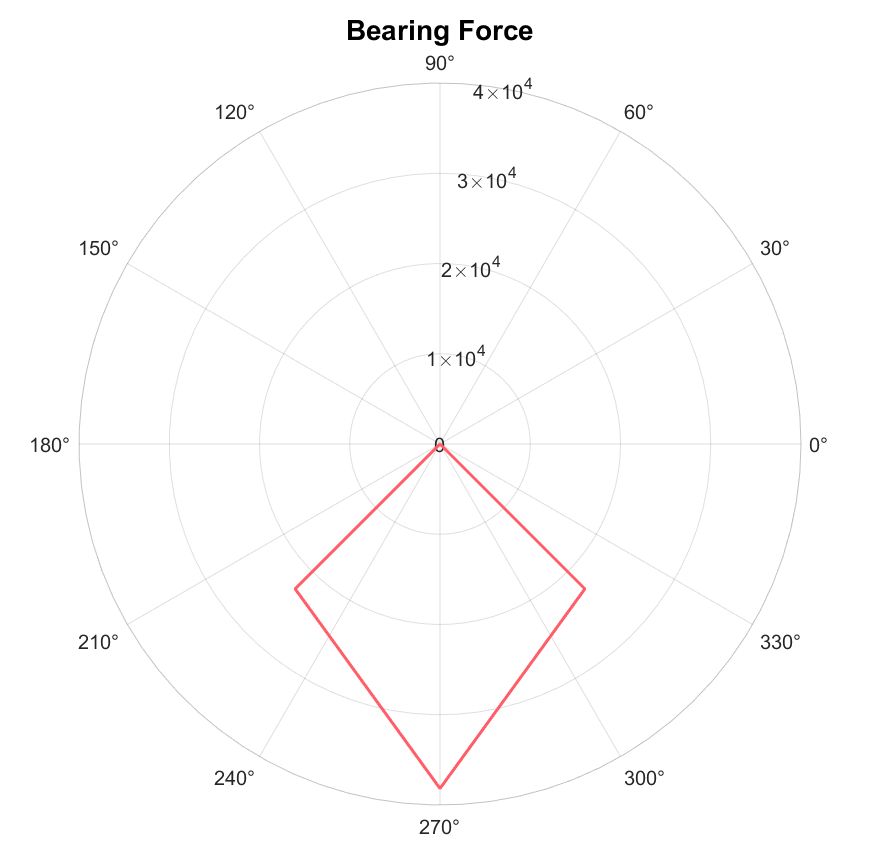
有限元模型
对于有限元模型,我们需要抓取内外滚道的中心,并于中心点建立弹簧。
有限元模型:
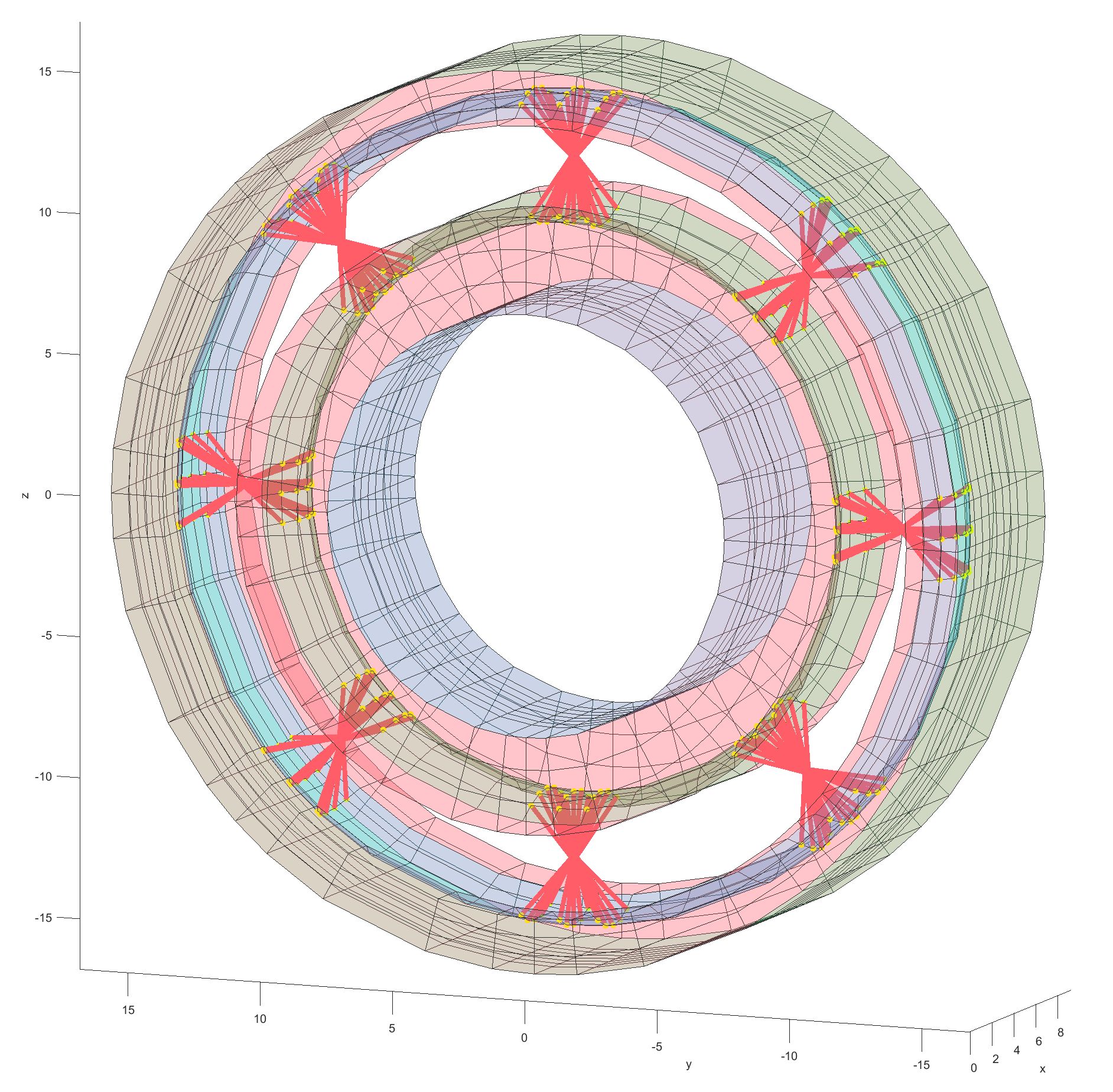
球滚子连接: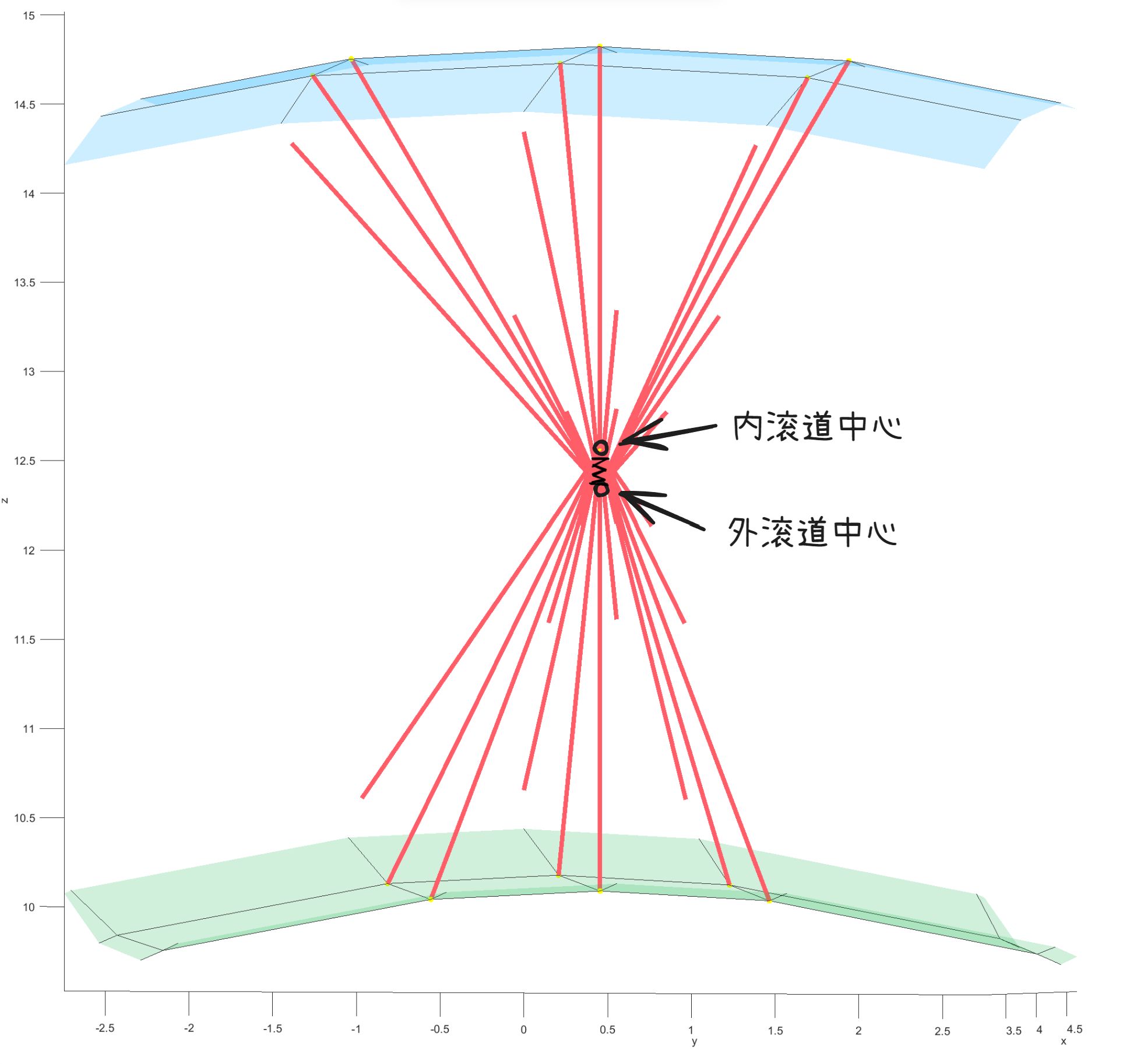
在仿真中,由于弹簧连接两滚道的中心,随着外载荷的变化,弹簧的受力始终沿着内外滚道中心的方向,即滚子接触角的方向,与球轴承的受力特点相符合。
由于深沟球轴承接触角变化不大,以下例子为角接触球轴承在推力作用下实体模型和弹簧模型接触角与外载荷的变化曲线,可以看出两者基本匹配。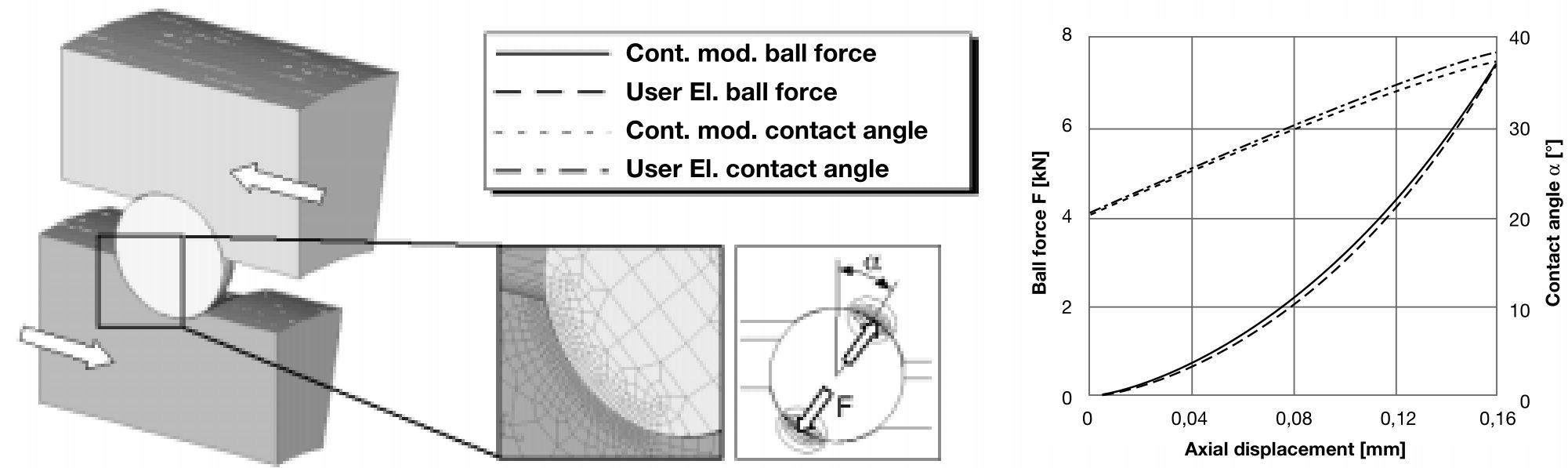
参考文献
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com