介绍
在之前的文章中介绍了纤维缠绕模块的开发,在确定完滑线系数、缠绕角后需要对整个部件的线型进行设计,使得缠绕的纤维均匀布满,这部分很多书籍和文献都没有介绍,本文将从最基本的数学原理介绍如何将纤维均匀布满。

一笔画多角星
首先,我们来讨论如何画一个五角星,这个问题非常简单,几何所有人都可以不假思索的画出如下图形:
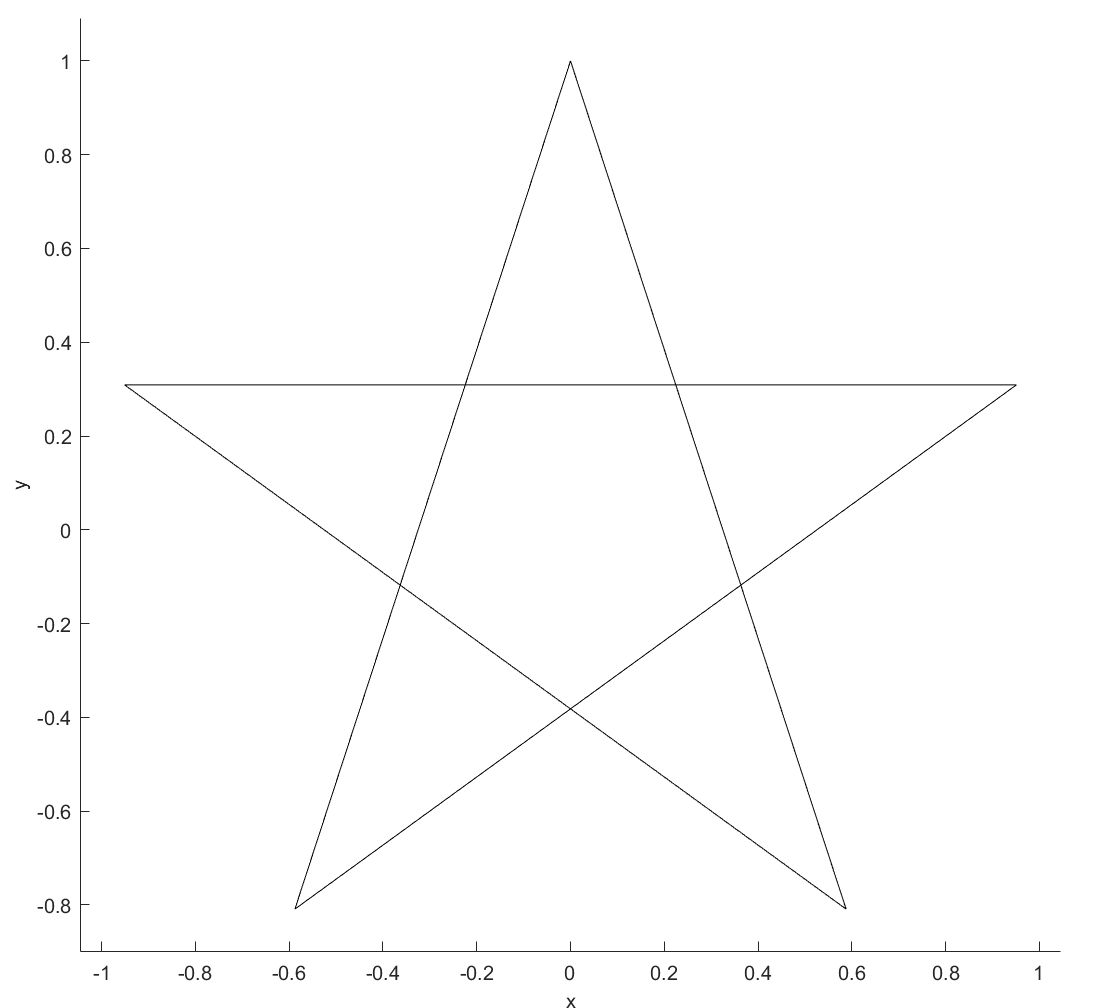
我们把多角星的角数定义为N, 把一条线跨过的角数称为P,
对于N=5角星,P=2、3,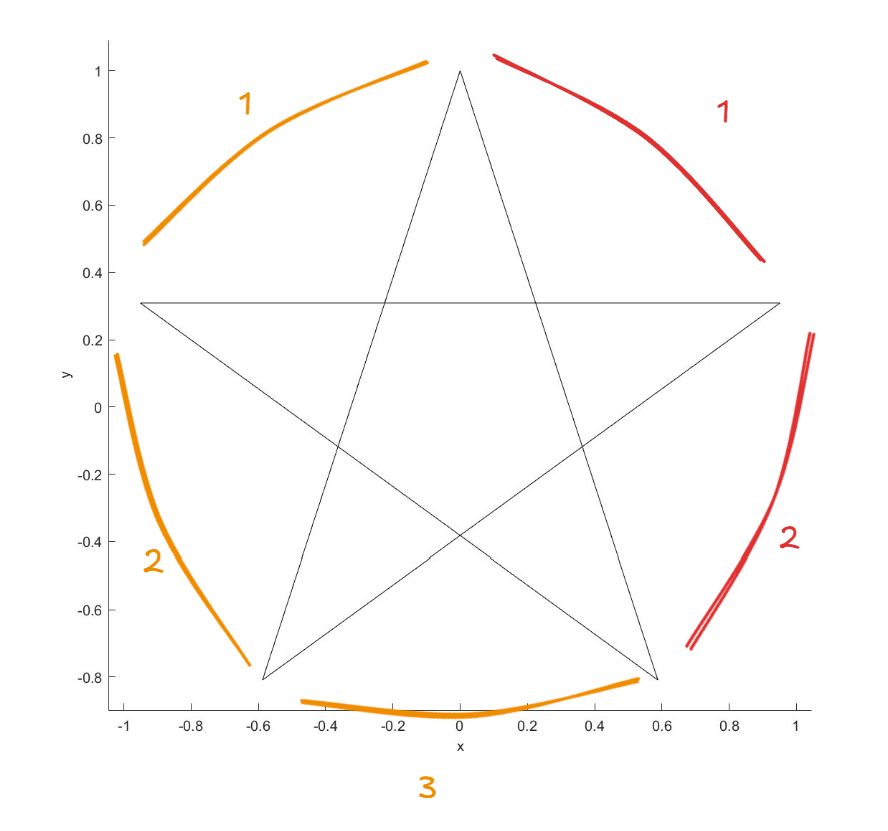
我们再来讨论六角星,当N=6时,P可以取2、3、4,但是很遗憾这几种组合均不能一笔画。
接着当N=7时,p取2、3、4、5,这几种组合都可以一笔画多角星。
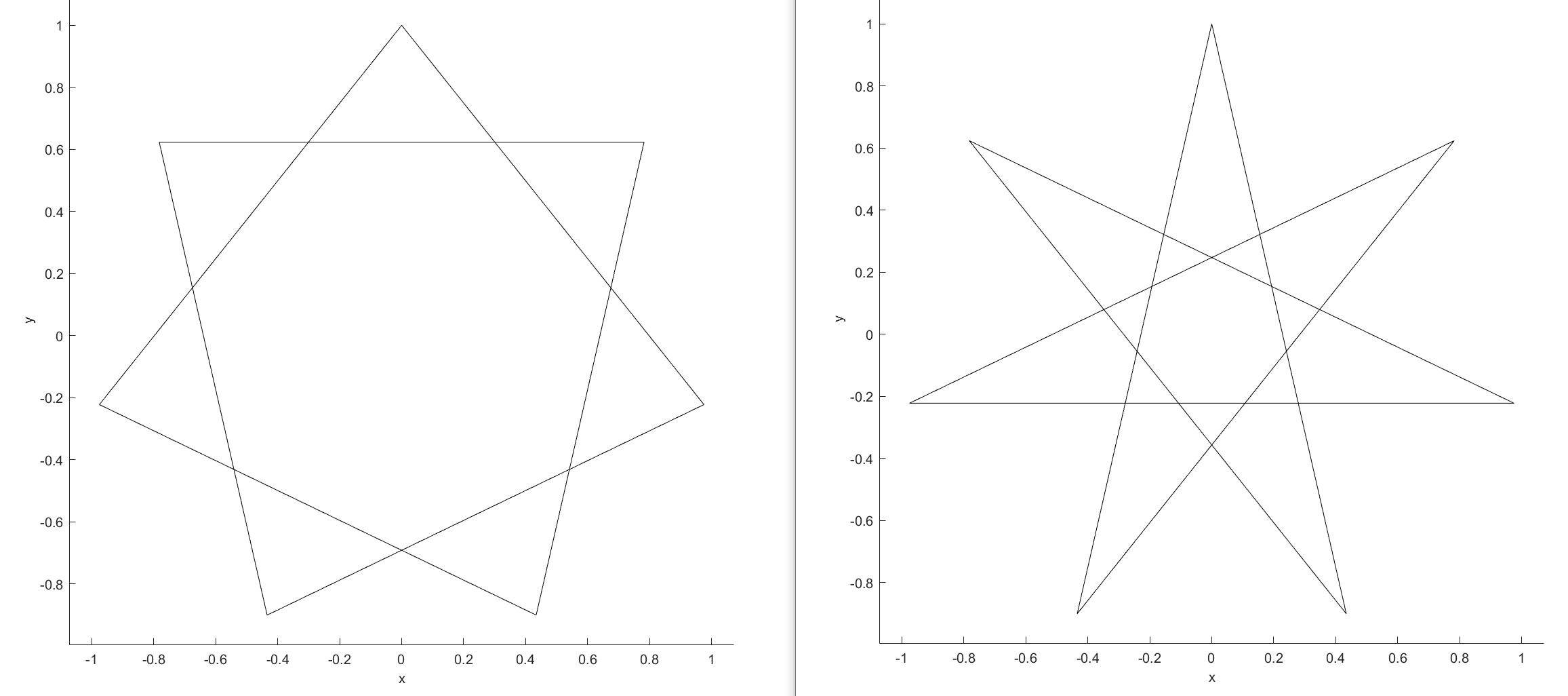
似乎当N为质数时,似乎更容易画出多角星,下一个质数是11,接着当N=11时,p取2、3、4、5、6、7、8、9,均可以稳定一笔画出。
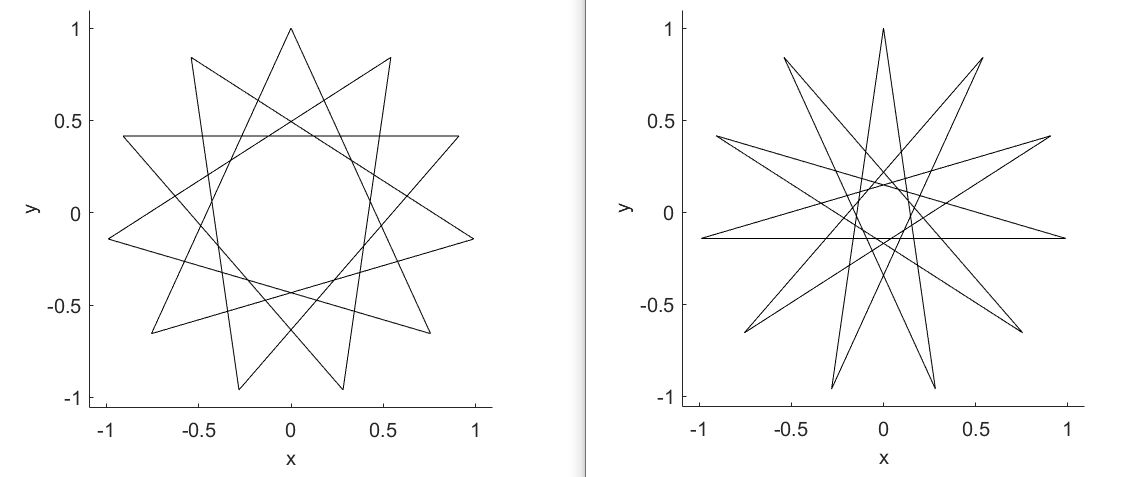
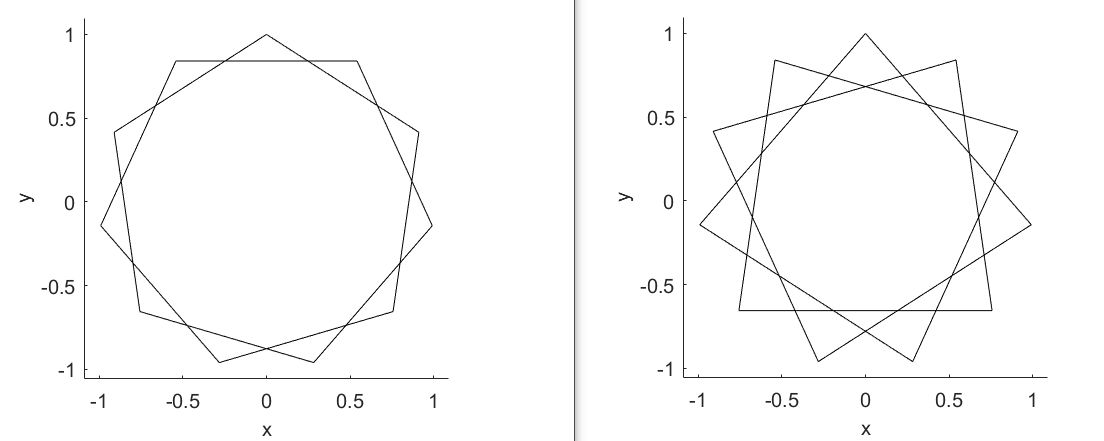
当N为质数时,其与任何数都互质,因此再绘图过程中,任何路径都不会与之前重复。
我们在回过头看N=6的情况,当P=2、3、4,N和P均可以找到公约数,因此六角星并不能一笔画成。
从多角星到线型分析
一笔画多角星可以归属到一个简单的图论问题,我们在把目光转回到纤维缠绕中,当纤维的带宽和缠绕角确定,我们可以计算起点处周长可以包含多少个带宽:
$$
N=\frac{2\pi R}{w/cos(\alpha)}
$$
式中,w为纤维带块,$\alpha$为缠绕角。在实际计算中,N选取最近的几个整数,这就满足了布满条件。
再运用上节提到的一笔画原理,不断搜索与N互质的P,这样就满足了均布条件。
我们以一个圆柱纤维缠绕为例: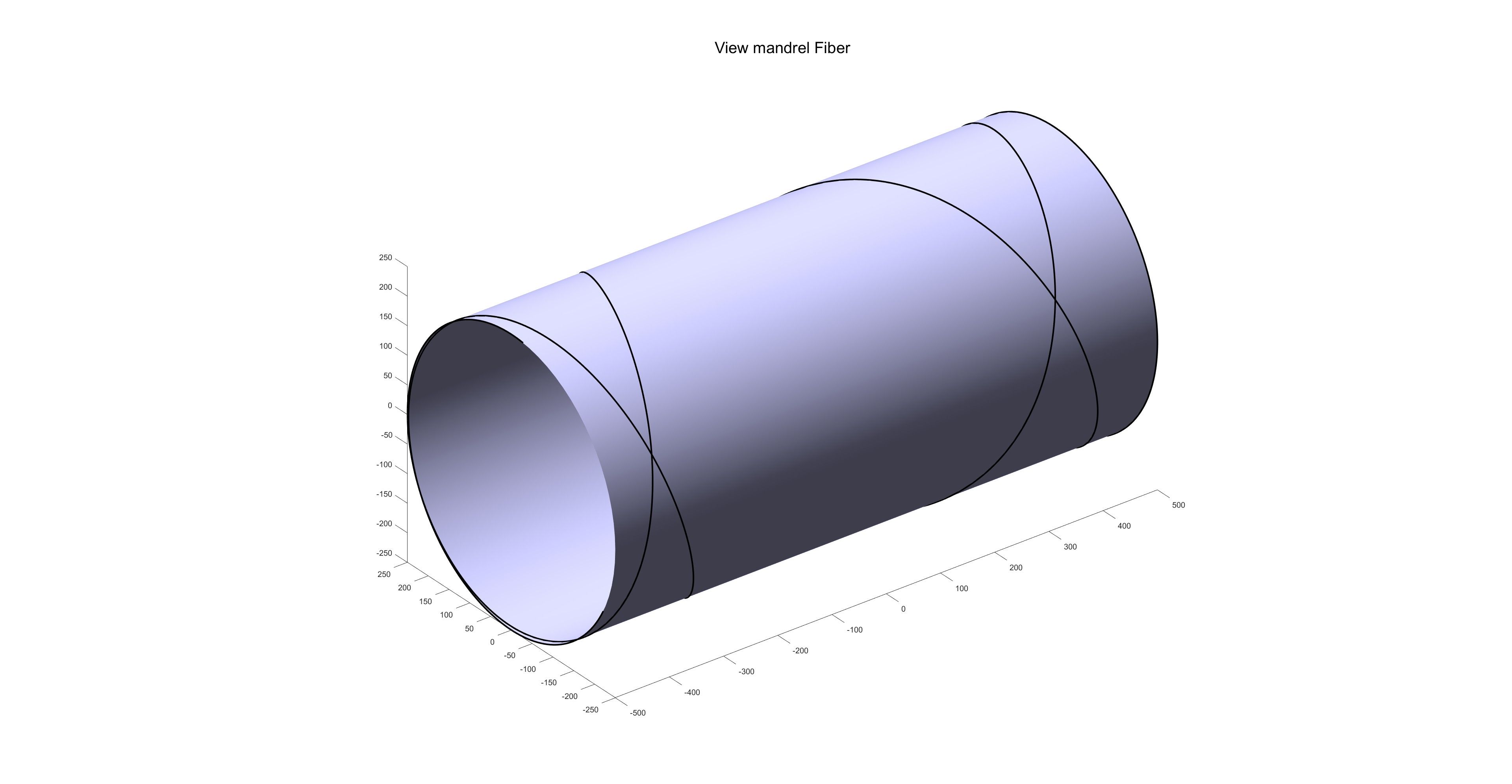
经过计算取N=47,其为一个质数,它与任何数互质,因为它有很多种方案可供选择,把所有方案绘制到一张图中:
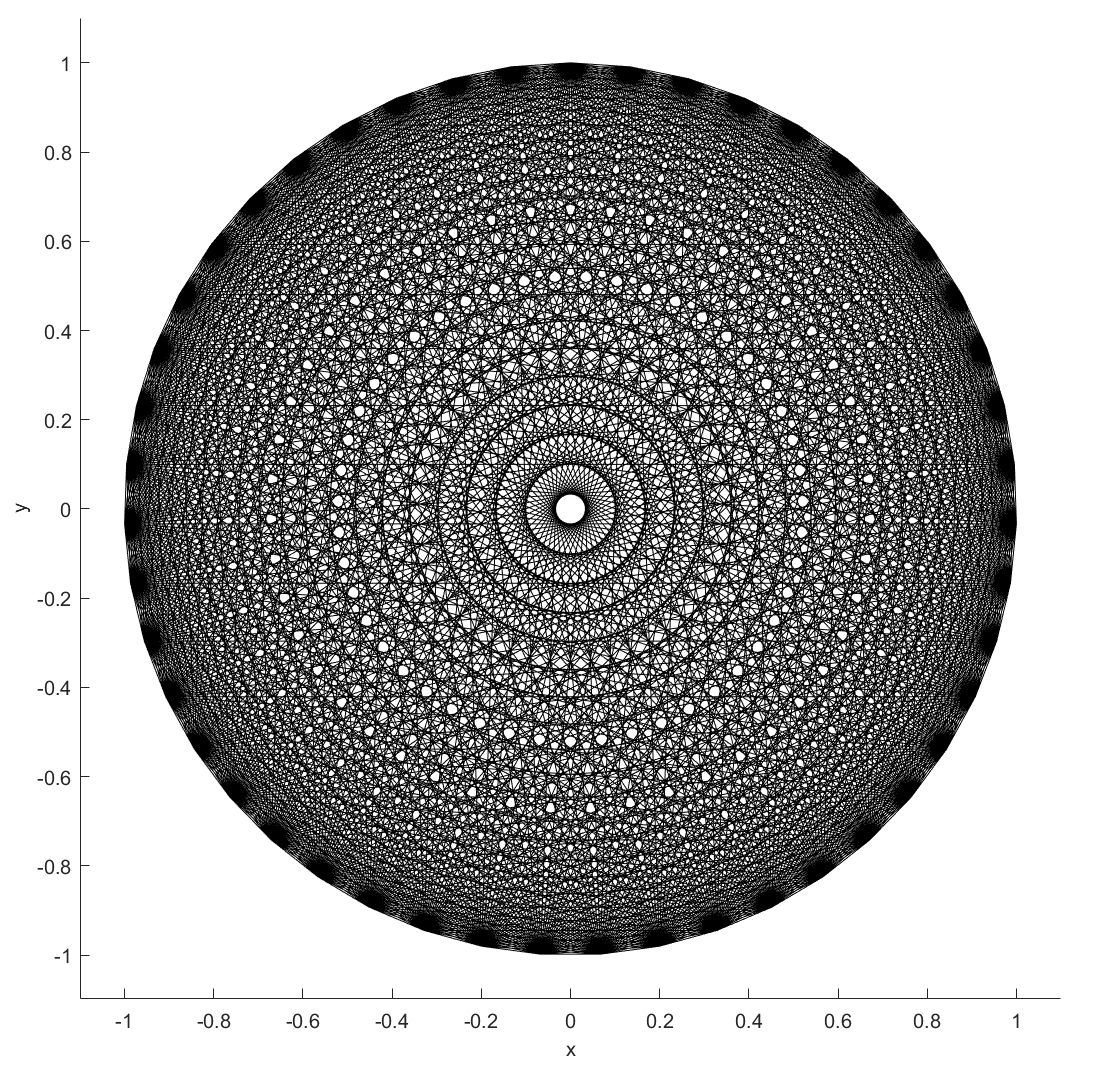
这里的方案很多,但在实际缠绕中,为了确保路径到达多角星的准确位置,需要90°缠绕角的尾端添加转接段,为了不让转接段纤维特别厚,尽量选择转接长度小的方案,因此在实际缠绕中,可供选择的方案并不多。
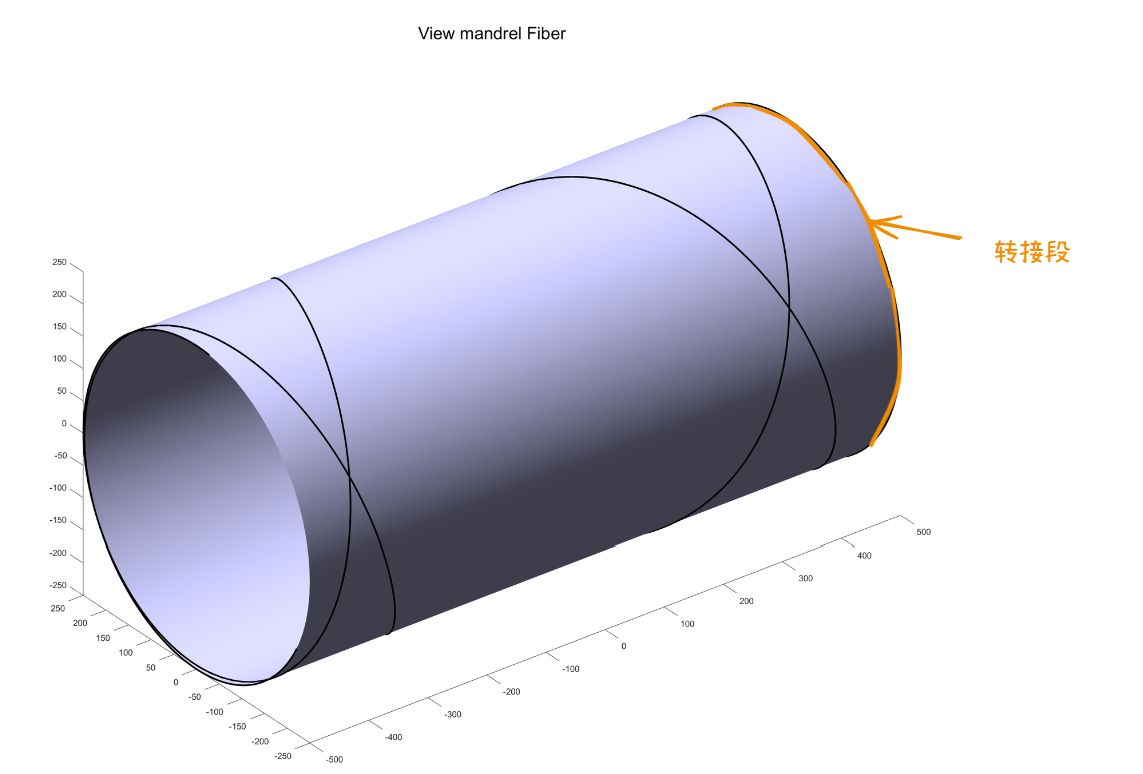
在确定完以上所有参数后,便可以初步在实际的项目中缠绕出满布均匀的部件。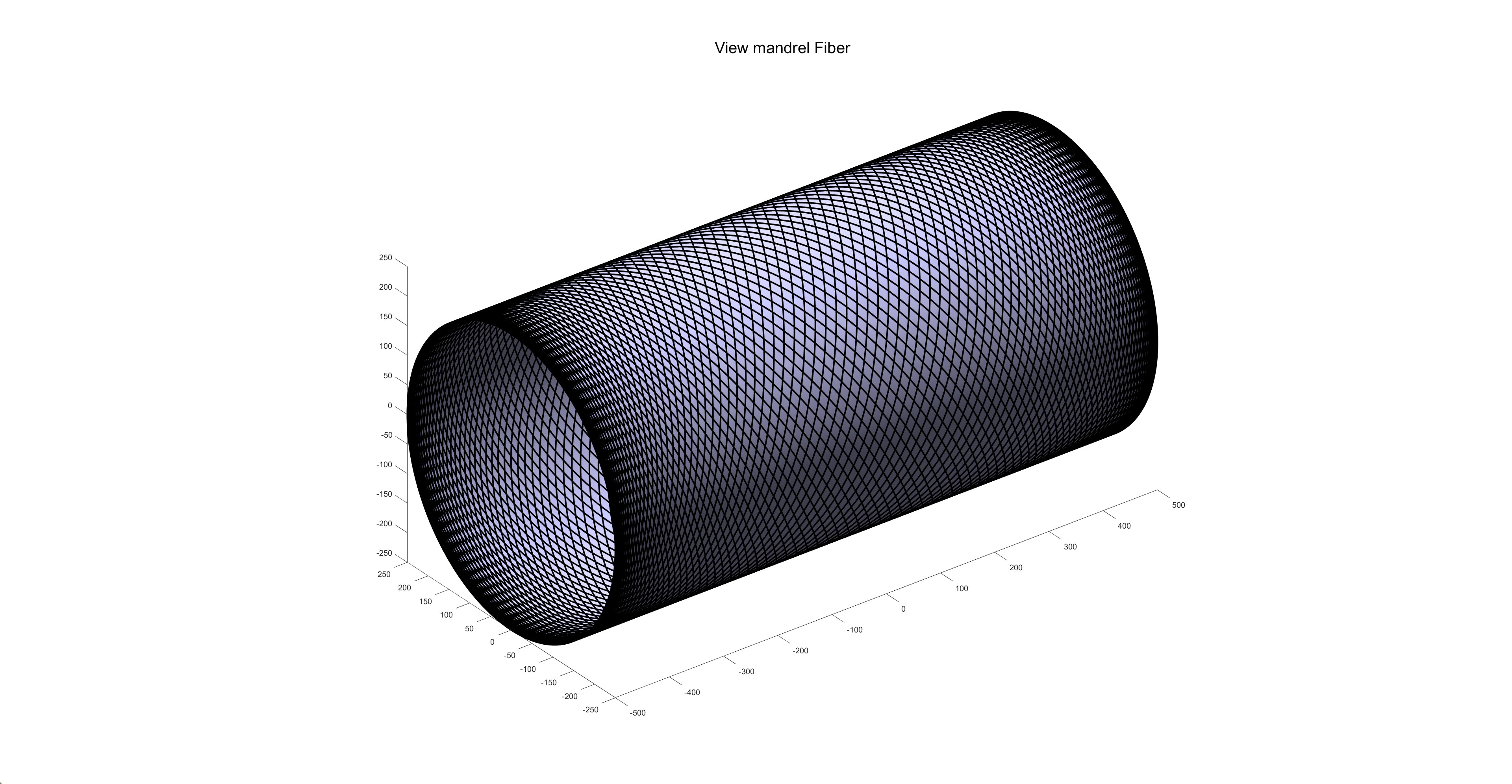
参考文献
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com