介绍
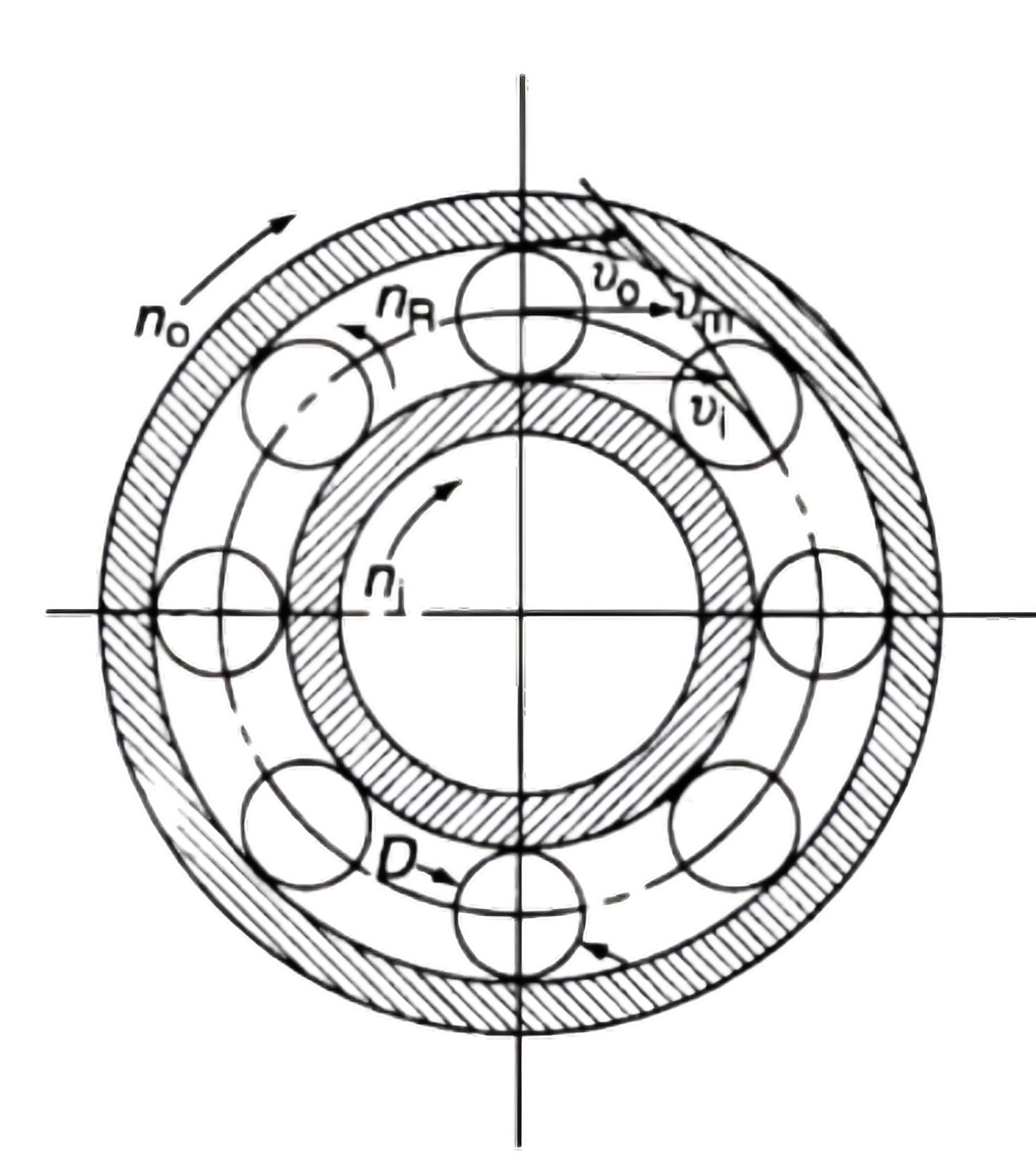
球或滚子轴承通常用于承受各种负荷,同时允许轴或滑块转动或平动。滚动轴承中的运动通常是一些复杂的运动。例如,一滚动轴承安装在转速为 $n$ (r/min) 的轴上,滚动体以转速 $n_m$(r/min) 绕轴承轴线转动,同时又以转速 $n_R$ (r/min) 绕自身轴线旋转。在多数工况下,特别是在轴承或外圈低速工况下,这些内部的速度能够运用简单的运动学关系式计算出足够精确的结果。
本文所讨论的情况是在低速/重载情况下,在这个限制条件下,可以略去轴承的动力学效应,比如球滚子的自身的陀螺和自旋效应。在高速的条件下,滚子自身受到离心力,这种情况下轴承运动会更为复杂。
为什么要理解轴承的运动学?
首先轴承的结构参数直接影响其运动学特性,比如滚子挡边的设计直接与滚子运动相关,同时我在之前的文章中介绍了滚道次表面的应力[2],如果我们得到滚子旋转一周对滚道某位置次数,是不是就能知道在整个生命周期中,该位置次表面的应力幅值、循环次数的信息。再进一步讲,如果我有了次表面剪力的SN曲线,那么我们可以通过SN曲线来计算轴承寿命。
其次轴承的异常运动往往是故障的早期信号,运动学分析为故障诊断提供了关键依据,结合运动学参数(如转速波动、冲击频率)与振动信号分析,可建立寿命预测模型。
另外在我们也可以人为的施加一些缺陷,在之前的文章中介绍了滚子和球的弹簧模型[3],[4], 如果滚道出现一个缺陷,当滚子经过滚道时,将该滚子的刚度降低,通过拟动力学的方式可以在仿真中复现缺陷的影响。
保持架转速
首先假定轴承内圈和外圈同时旋转,内外圈具有相同接触角$\alpha$ 。绕轴旋转的线速度为:
$$
v=\omega r
$$
由此可以推算出内圈的线速度:
$$
v_i=\frac{1}{2} \omega_i(d_m-Dcos\alpha)=\frac{1}{2} \omega_i d_m(1-\gamma)
$$
同理外圈线速度为:
$$
v_0=\frac{1}{2}\omega_od_m(1+\gamma)
$$
如果滚子和滚道没有严重的滑动,保持架和滚动体的线速度为内圈和外圈速度的平均值:
$$
v_m=\frac{1}{2}(v_i+v_o)
$$
进一步整理可得,内圈、外圈和转架的转速关系:
$$
n_m=\frac{1}{2}[n_i(1-\gamma)+n_0(1+\gamma)]
$$
滚动体转速
保持架相对于内圈的角速度是:
$$
N_{mi}=n_m-n_i
$$
假定内圈滚道和球接触处没有严重的滑动,接触点上球的线速度等于滚道的线速度,于是:
$$
v_m=\frac{1}{2} \omega_md_m(1-\gamma)=\frac{1}{2} \omega_RD
$$
因为n正比于$\omega$, 带入得到:
$$
n_R=(n_m-n_i)\frac{d_m}{D}(1-\gamma)
$$
整理得到滚动体自转的转速为:
$$
n_R=\frac{d_m}{2D}(1-\gamma)(1+\gamma)(n_0-n_i)
$$
应用简介
我们将运动学简单应用到计算中,如下图所示是内滚道某一位置在运动过程中发生接触统计,可以看到一次循环为97转。
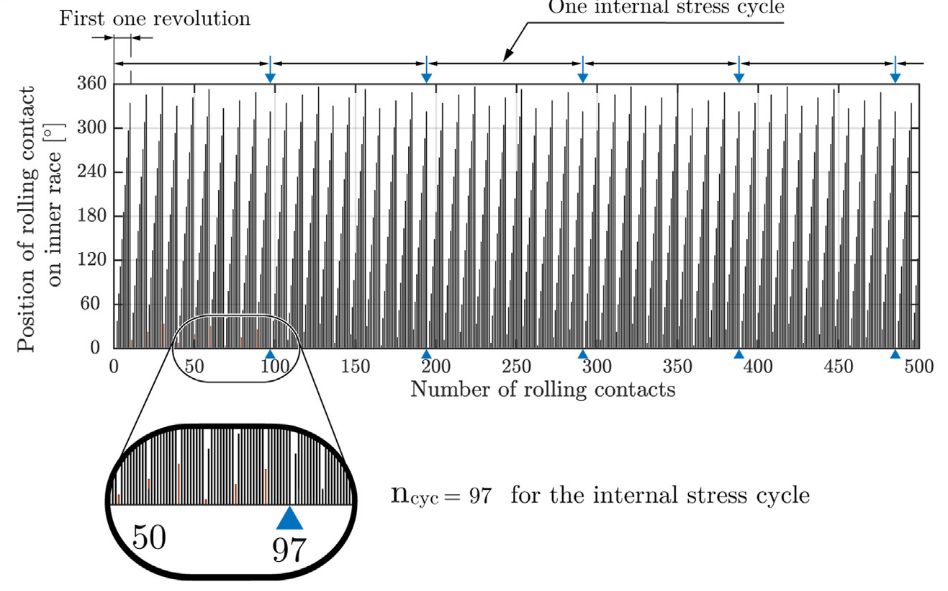
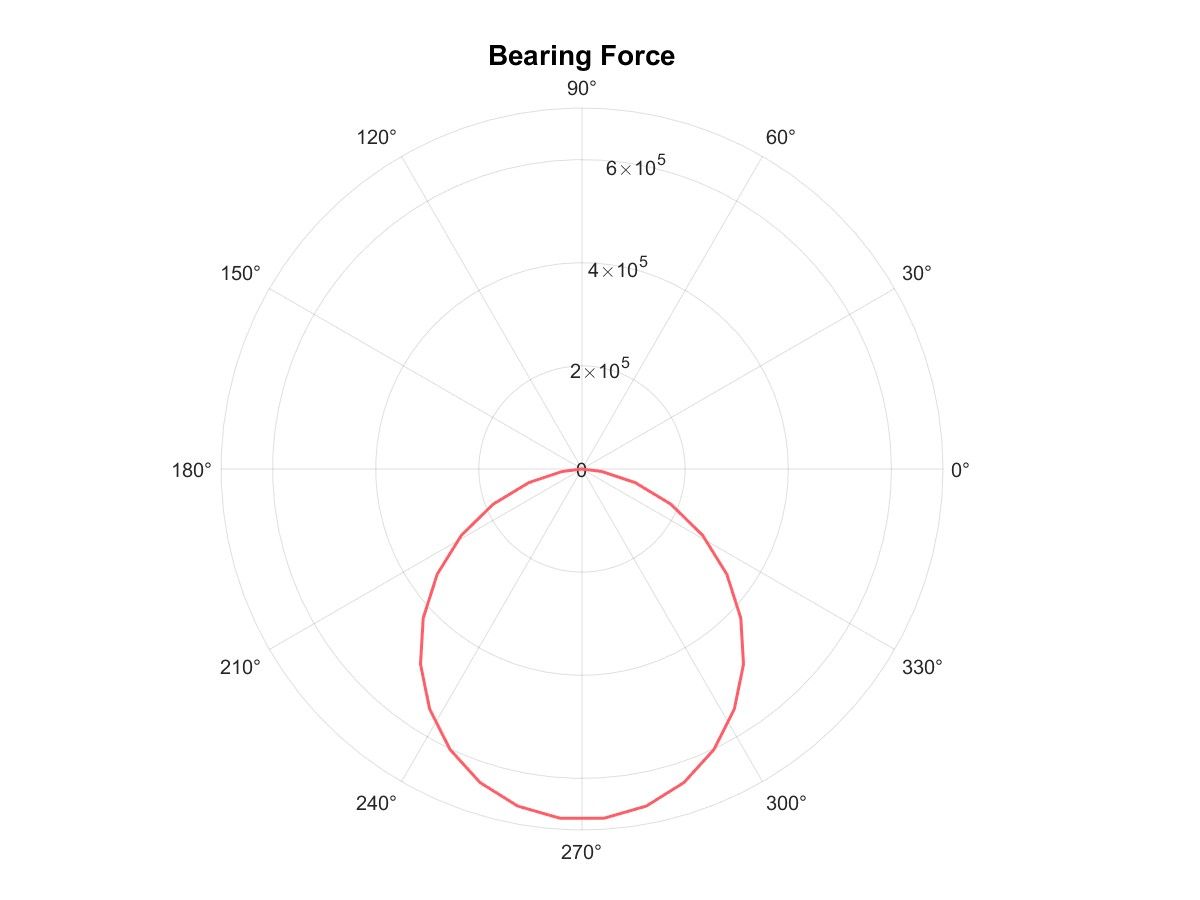
如果整个系统载荷方向和大小保持不变,那么载荷与接触位置是相关的,比如在270°位置对应载荷最大,那么90°位置载荷几乎为0,根据这个关系就可以得到次表面的应力循环次数和应力幅值。再加上材料的SN曲线,便可以应用传统疲劳设计的方式计算轴承寿命。
参考文献
[1] 滚动轴承分析
[2] https://www.feacat.com/2025/07/15/%E8%B5%AB%E5%85%B9%E6%8E%A5%E8%A7%A6%E5%92%8C%E6%AC%A1%E8%A1%A8%E9%9D%A2%E5%BA%94%E5%8A%9B%E5%88%86%E6%9E%90/
[3] https://www.feacat.com/2025/08/11/%E6%BB%9A%E5%AD%90%E8%BD%B4%E6%89%BF%E5%BB%BA%E6%A8%A1%E4%B8%8E%E8%AE%A1%E7%AE%97%E4%BB%BF%E7%9C%9F/
[4] https://www.feacat.com/2025/08/19/%E7%90%83%E8%BD%B4%E6%89%BF%E8%AE%A1%E7%AE%97%E4%B8%8E%E5%BB%BA%E6%A8%A1%E4%BB%BF%E7%9C%9F/
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com