介绍
在纤维缠绕轨迹规划中,为了保证纤维的稳定缠绕,必须要满足两个条件:
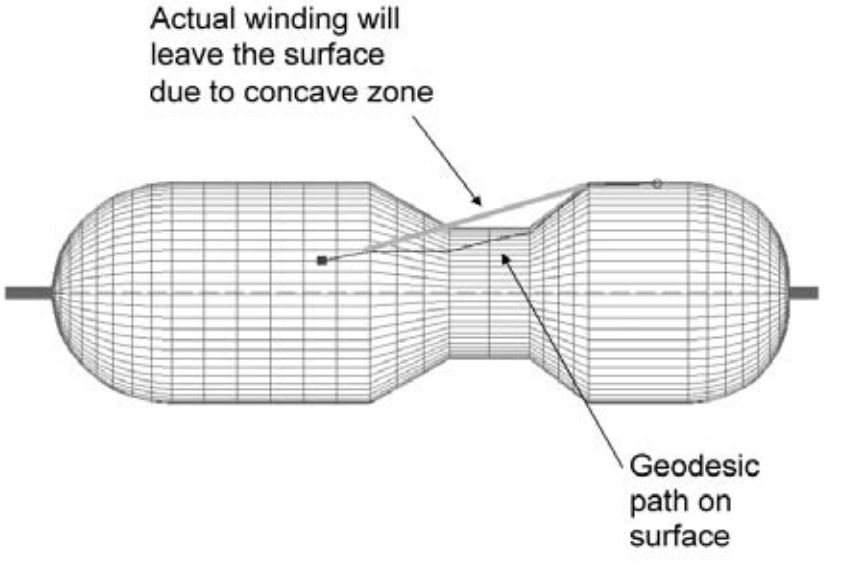
- 不架空条件,即纤维紧贴在芯模表面,纤维应稳定存在并不产生滑动而偏离轨迹,如下图所示。
- 不滑线条件,即按设计轨迹将纤维缠绕到芯模表面,纤维应稳定存在并不产生滑动
纤维受力分析
为了计算纤维的稳定性,首先需要精准的计算缠绕纤维的受力。
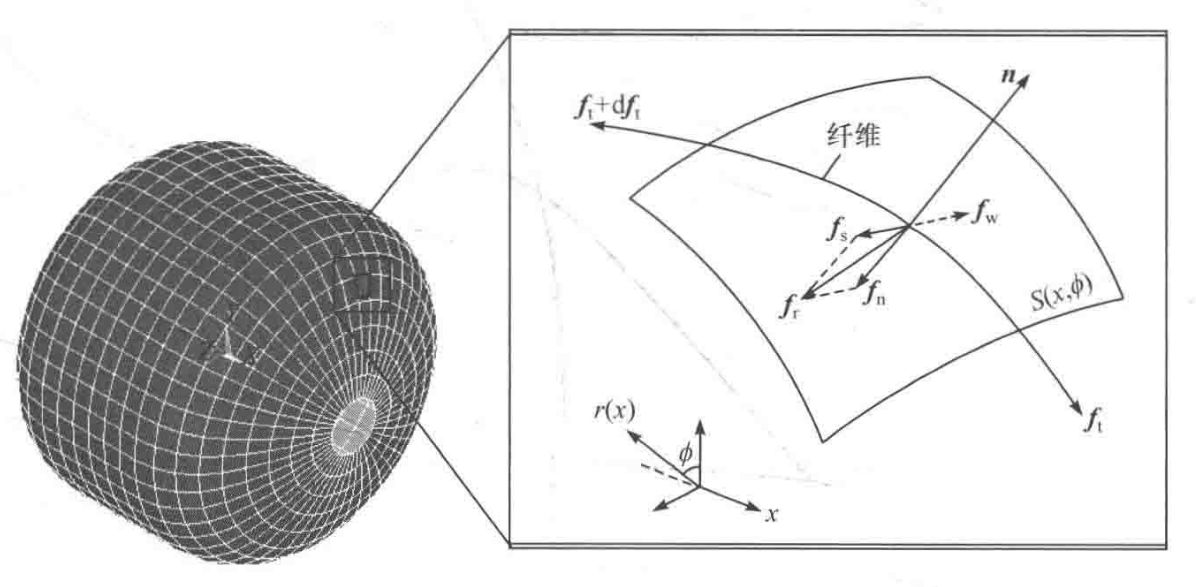
在芯模表面任取一段微元,沿着纤维方向每单位长度上会产生一个力:
$$
f_r=f_t · da(s)/ds
$$
式中,$f_r$为纤维方向每单位长度上的力;$f_t$为缠绕张力;$da(s)$为纤维微端上点的切矢量;$da(s)/ds$为纤维轨迹的曲率矢量。
$fr$可以分解为曲线法向n上的投影分量正压力$f_n$和在切平面上的投影分量侧滑力$f_s$。正是由于侧滑力$f_s$的存在,所以纤维有滑动的趋势。
根据纤维轨迹的曲率矢量:
$$
\frac{da(s)}{ds}=f_tk\gamma
$$
$k$为纤维轨迹的曲率,$\gamma$为纤维轨迹的主法矢。
该合力$f_r$在纤维轨迹法矢上的投影分量的正压力$f_n$为:
$$
f_n=f_t k_n
$$
在切矢量上的投影分量正压力$f_s$为:
$$
f_s=f_tk_g
$$
式中,$k_n$为曲面法曲率,$k_g$是曲面测地曲率。
不架空条件
在缠绕过程中,要使得纤维不架空,当$k_n$为正,正压力$f_n$与法矢同向,其作用会让缠绕纤维脱离芯模表面,易导致架空现象的产生。因此要使得纤维不架空的先决条件是$k_n<0$
不滑线条件
在缠绕过程中纤维所受的摩擦力$f_w$需要克服侧滑力$f_s$, 此时需要满足:
$$
|f_s| \le |f_w|
$$
令缠绕纤维与芯模表面间的摩擦系数为$\mu$,则摩擦力$f_w$等于:
$$
|f_w|=\mu|f_n|
$$
联立上述公式,可以得到缠绕的稳定不滑线条件:
$$
\mu \ge|k_g|/|k_n|
$$
计算案例
我们以一个压力容器为例,正常以60°缠绕角缠绕的效果如下,可以看到两边有很多空余。
为此,笔者在Baffalo中的Filamentwinding模块更改了路径搜索策略,当缠绕角在端部达到90°时,减小一定的角度,并满足不滑线条件,当角度减小到一定程度,再增加角度到90°,来让纤维能缠绕到端部。
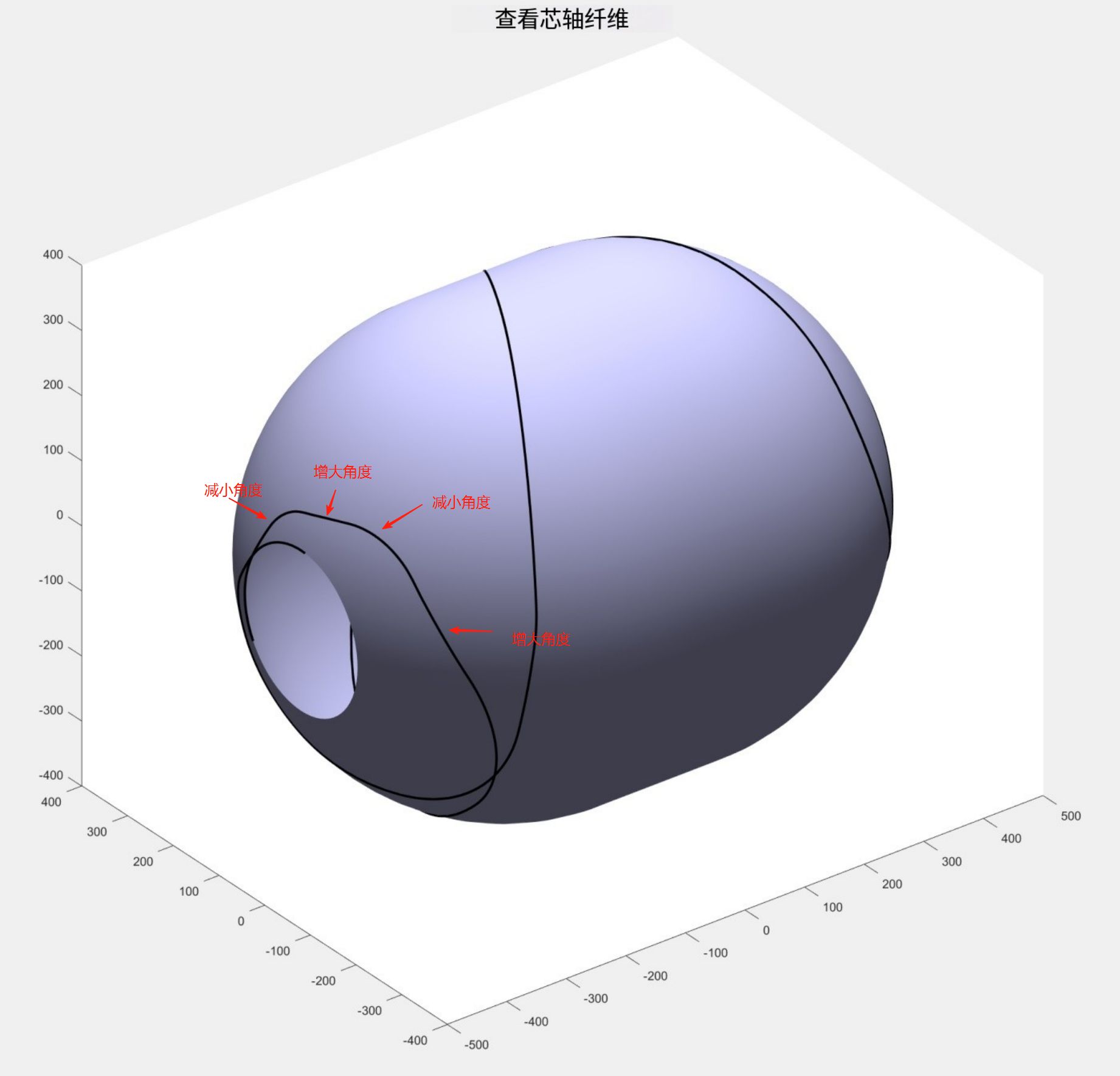
这种缠绕方式在数学上是满足不滑线条件,但在实际中也是很难实现的。由此笔者认为还存在另外的限制条件厚度,由下图可以清晰的看到,在缠绕角到达90°角度左右,很容易产生纤维的积聚。
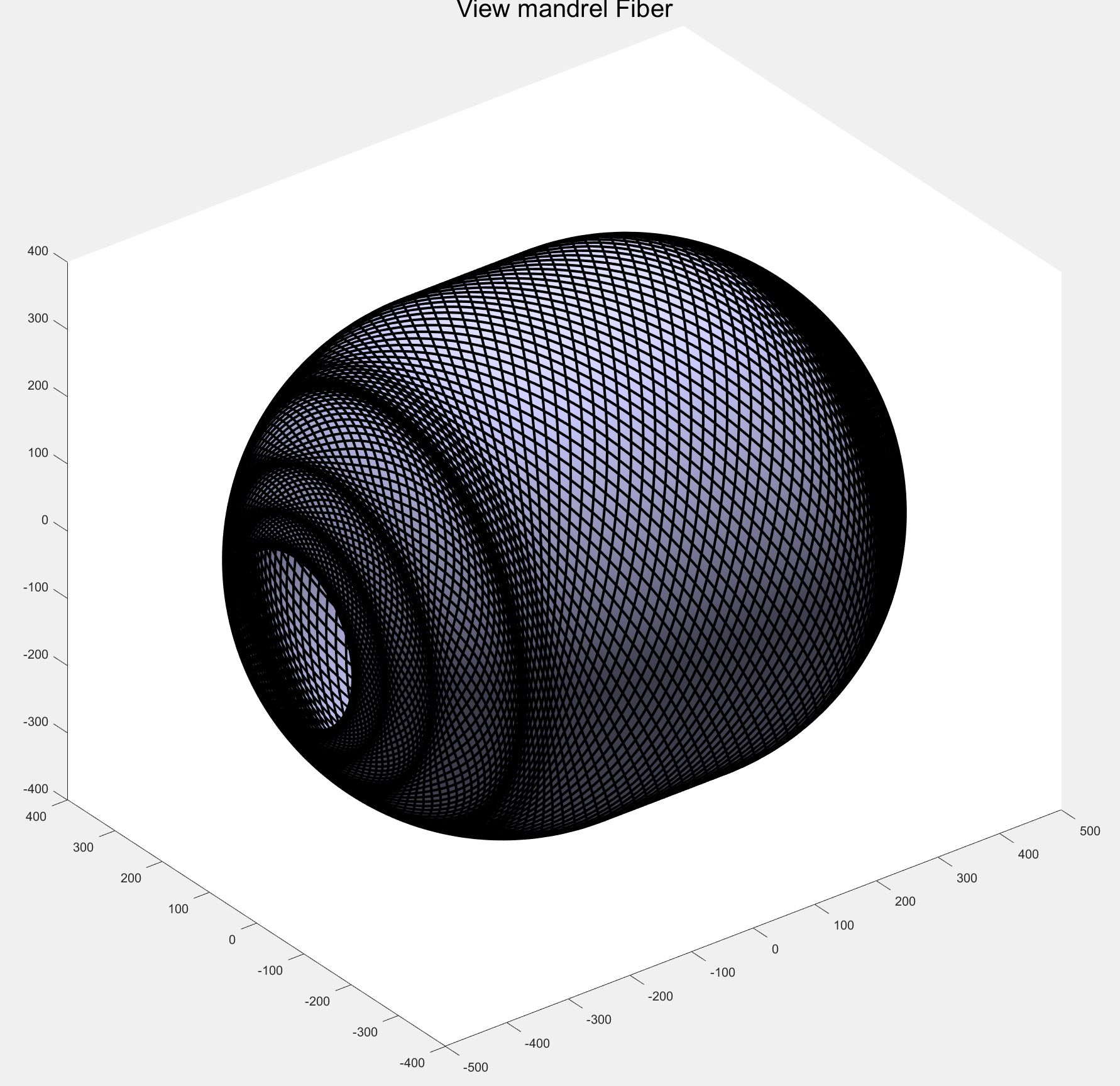
由此会形成类似于小山坡的形状,从而阻止纤维继续向端部发展,如果想要越过这座山坡,必然会带来额外的缺陷。
Baffalo中可对厚度进行估算,由下图可以看到在往端部进行缠绕的过程中,会产生4个凸起,这也导致了其很难保证工艺的稳定性。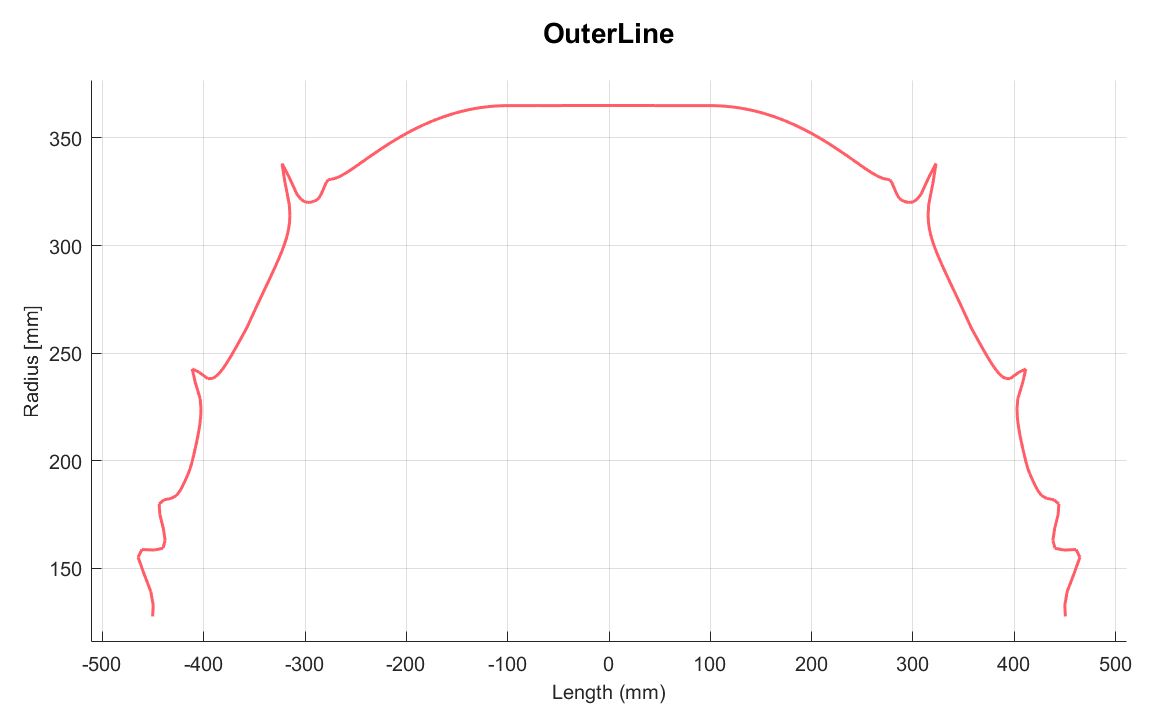
因此,纤维缠绕在不满足不架空、不滑线的条件下,在某些情况下,笔者认为还需考虑由外形带来不确定性,以确保缠绕的稳定。
参考文献
[1] 先进复合材料压力容器
[2] https://www.feacat.com/2025/08/15/FilamentWinding/
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com