介绍
渐开线齿轮是现代常用的机械零件,目前几乎所有的齿轮设计书籍会直接告诉你一堆复杂的公式,却忽视思考的核心。本文从传动正向设计的角度出发,带来渐开线齿轮的一些思考,也希望给你一些启发。
传动
首先从最朴实的想法出发,设计一个传动系统,希望两个轴系之间实现转速的传递。同时希望保持传动的平稳,也就是说两个轴系间的力大小和方向都不随时间改变。
这似乎很简单,我们设计两个圆,圆的半径不随转角的变化而变化,也就说力的方向不会变化。我们给两个圆施加一定的初始压力,让他们靠摩擦传力,这样力的方向也不会变化。这样我们就设计了一个精巧的传动系统,传力平稳可靠。
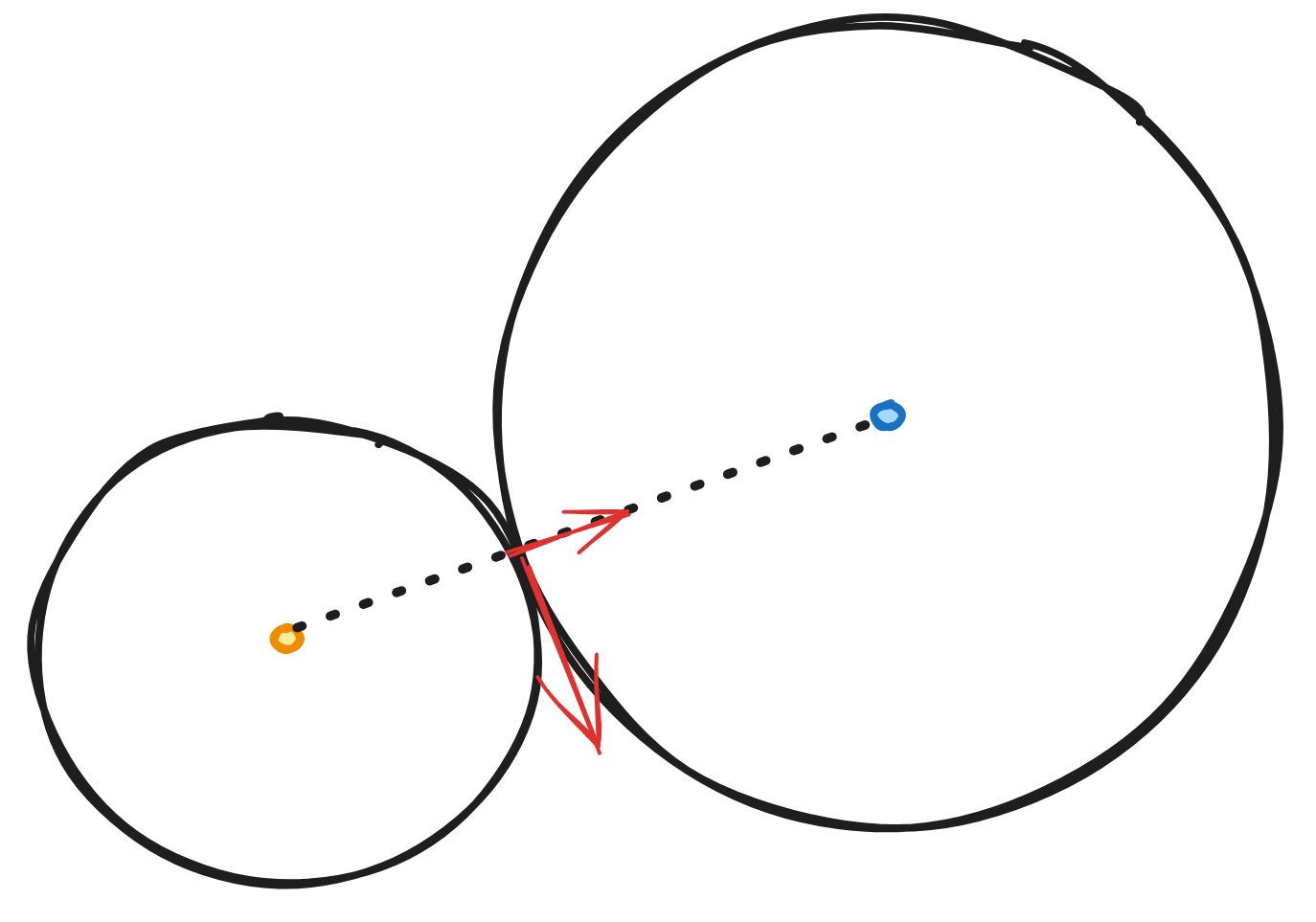
但是在使用过程中,两个圆会随着时间的发展而磨损,剪切力也不能设计的很大,导致整个传动系统非常的脆弱。
从剪力到压力
既然剪力传力使得系统很脆弱,能不能把剪力改为压力呢?压力由两个面接触,他的承载力是摩擦力的6~8倍。于是乎,我们便将两个圆接触的地方改成齿槽状。
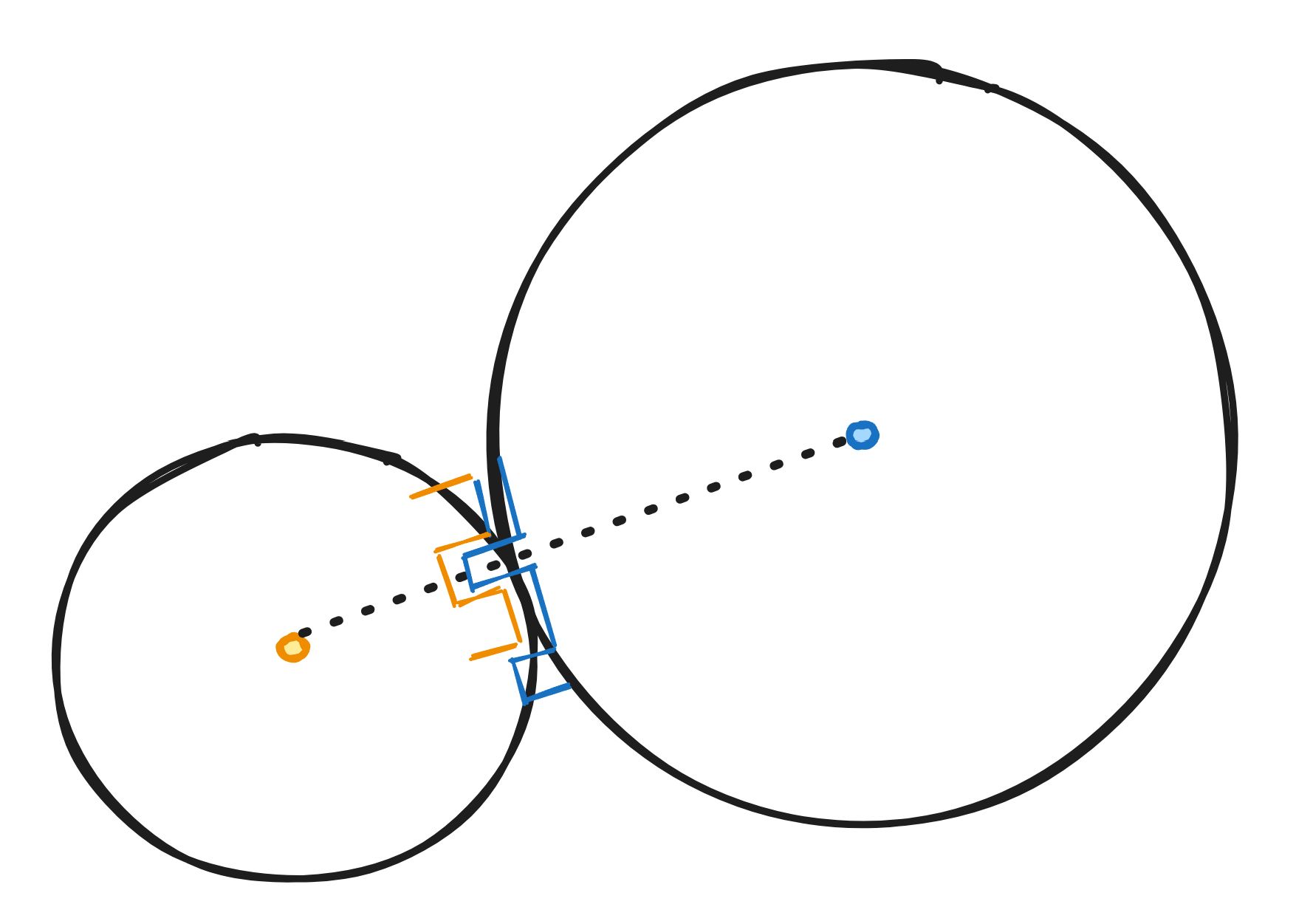
承载力是解决了,但是却忽略了传动的基本条件,当转动的过程中,接触压力的方向是变化的,也就说这样的设计会给整个系统带来额外的噪声和振动。
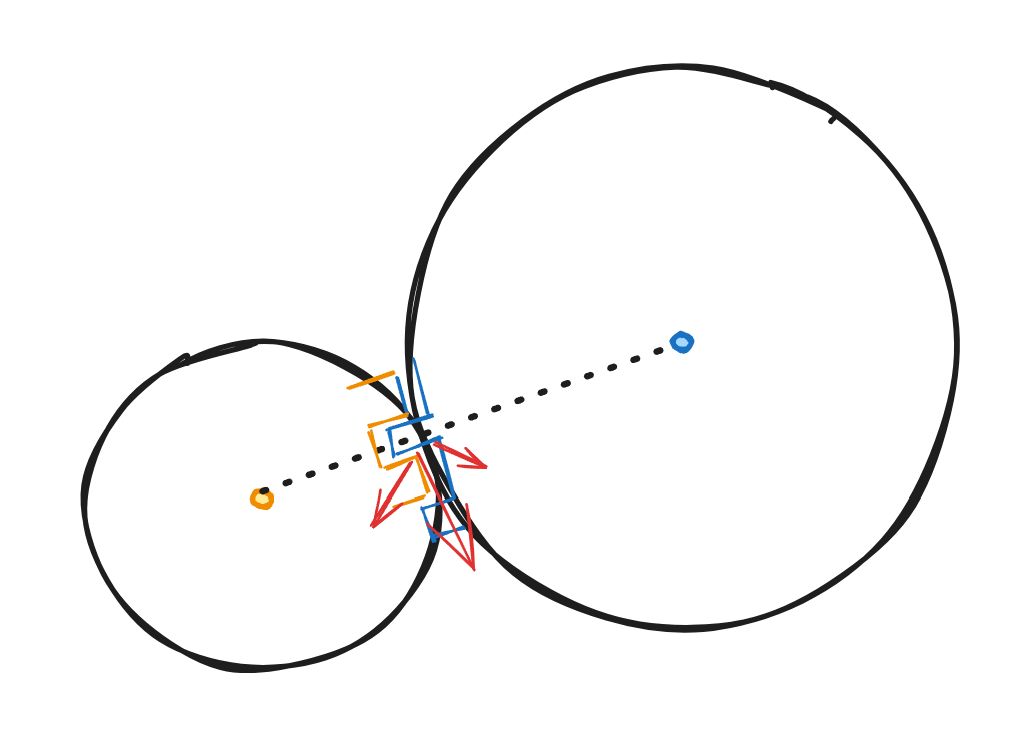
渐开线
我们既要靠压力传递又要让压力的方向始终不变,没有办法我们只能做一些妥协,要想保持上述两个条件,力的方向指向圆心是不可能的了,我们接触的法向移到两个圆的切线方向。
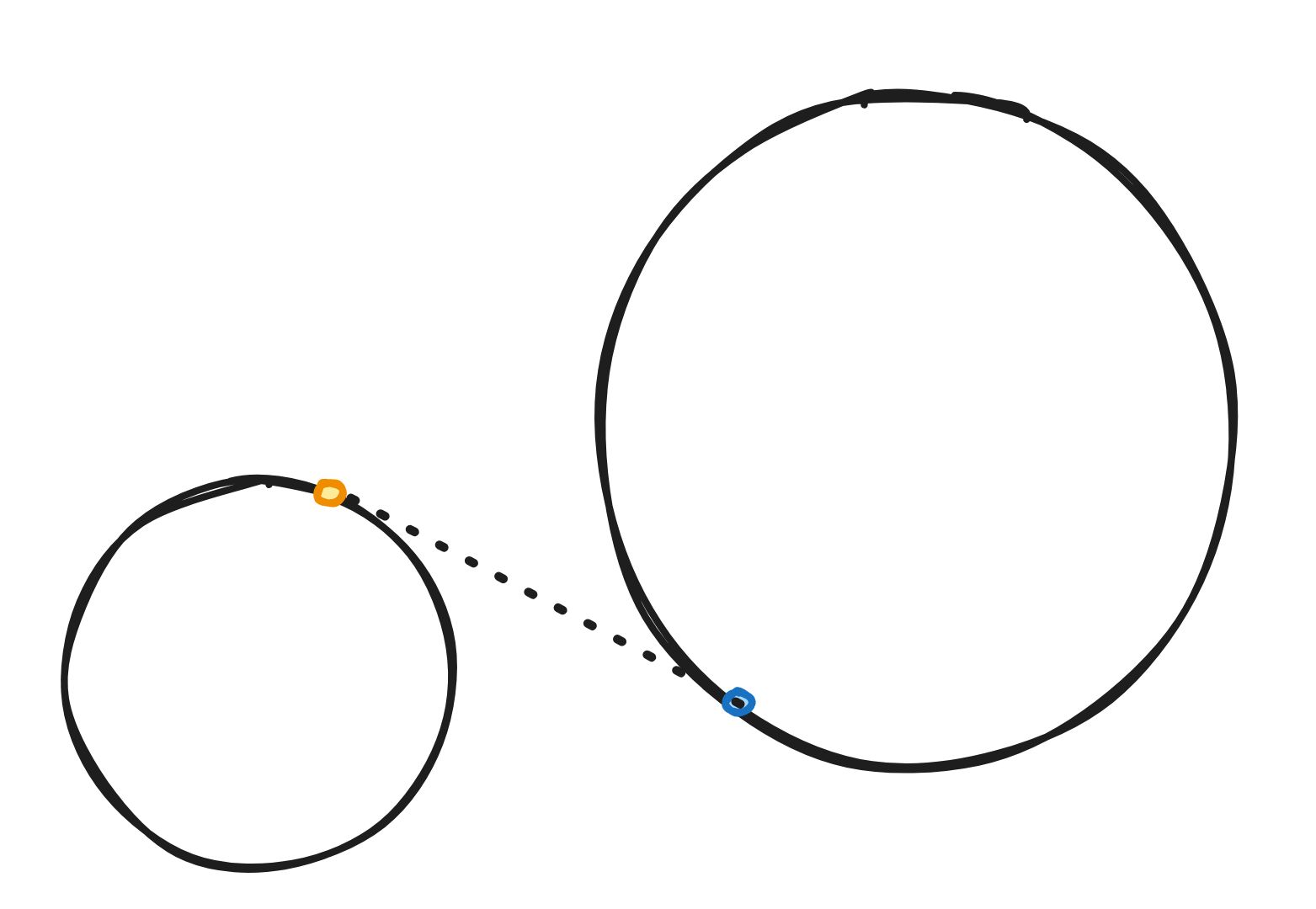
同时需要设计一个特殊的齿槽满足两个轴系时刻接触,保证传动的稳定。我们将啮合处的点的运动分解,他可以分为转动和直线的运动。
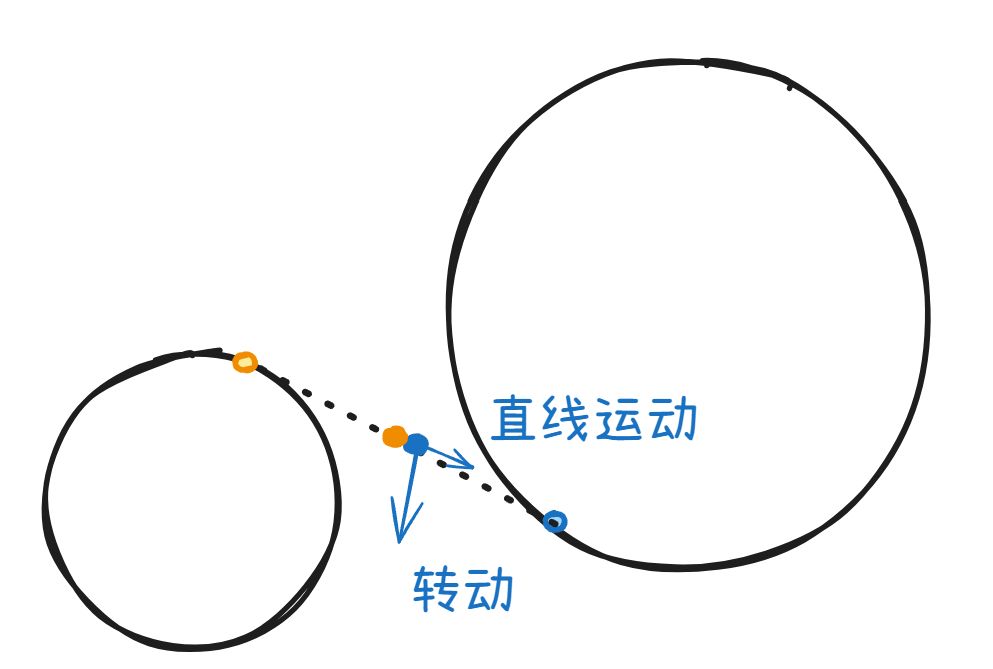
为例保证时刻啮合,当啮合处的点发生直线运动时,另一个轴系的啮合点必须将这部分位移给补偿掉。
最精彩的部分就来了,我们圆周上的点转动的同时,沿着切线方向给他个位移。
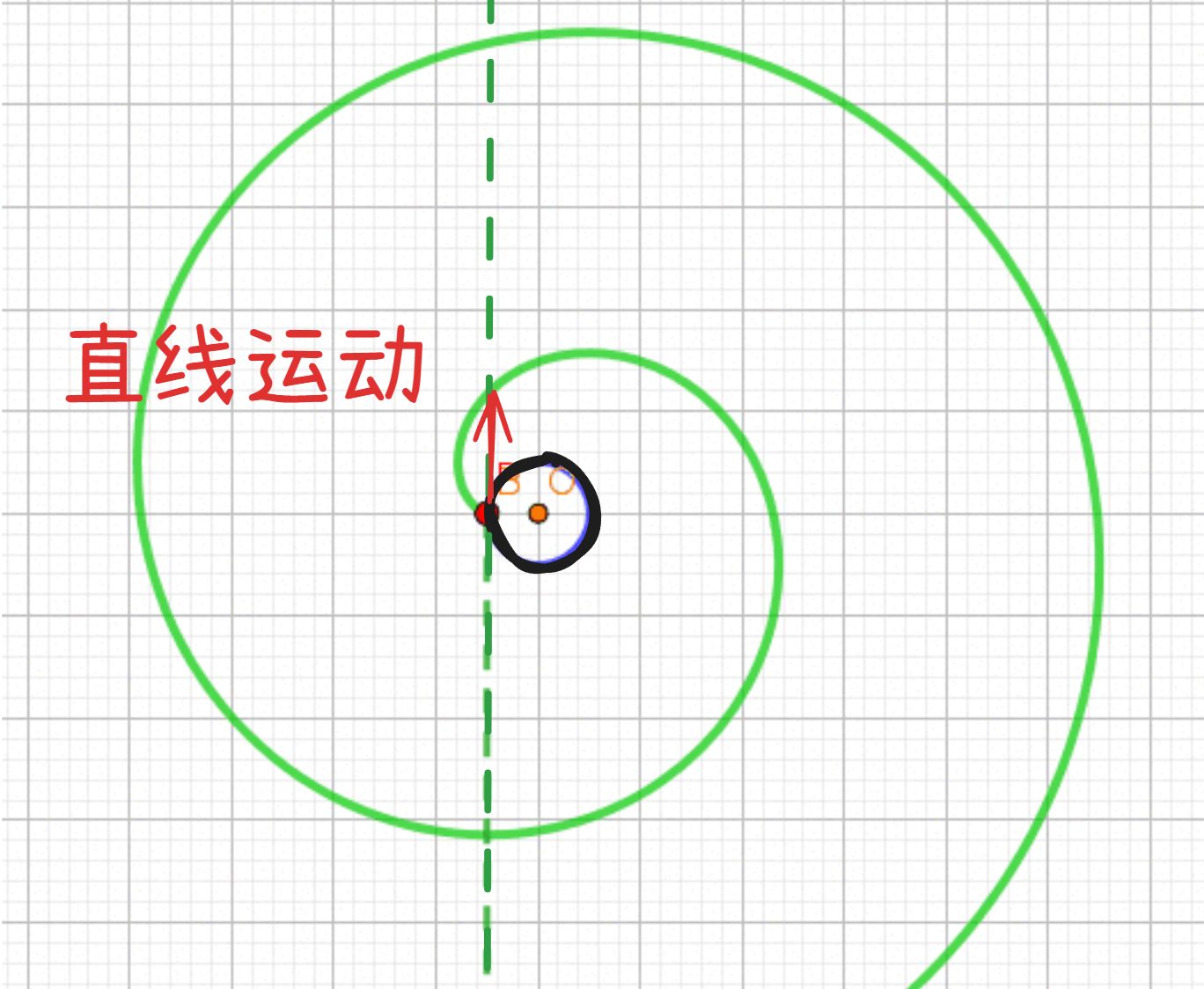
在回到原先两轴系运动分解的图中,因为两圆转动方向相反,一个圆直线向外扩张时,另一个圆刚好收缩,这样就能保证时刻啮合的条件,让传力平稳。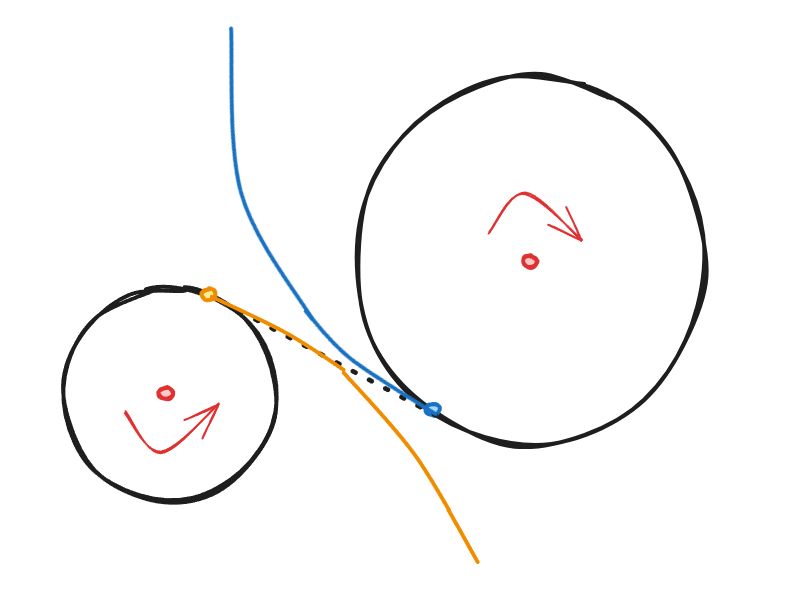
那么剩下的就是构造齿廓方程的时刻,下图中的 $inv \alpha$为渐开线的函数角,角$\theta$为渐开线的转动角。
$$
inv\alpha=tan\alpha-\alpha
$$
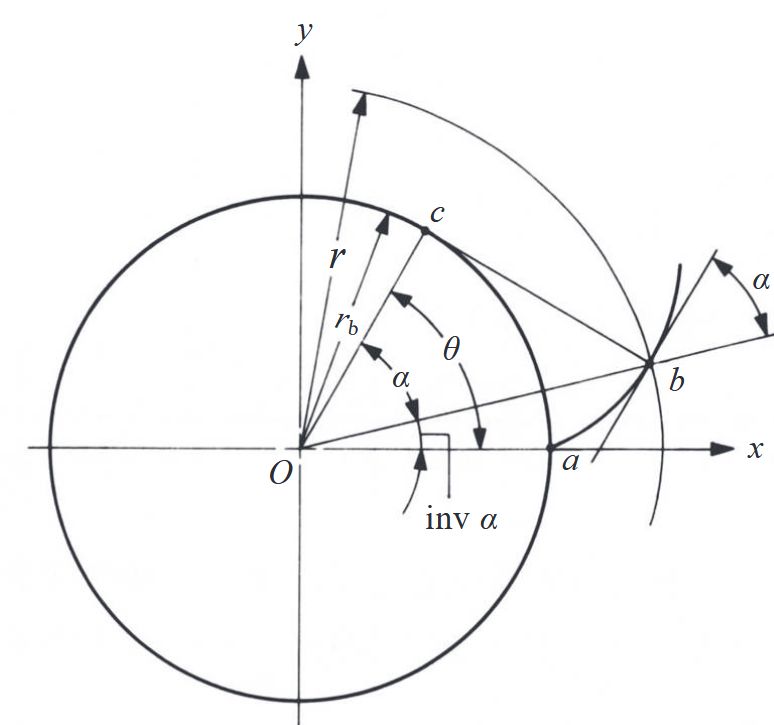
渐开线的公式如下:
$$
\alpha=cos^{-1}\frac{r_b}{r}
$$
$$
x=rcos(inv\alpha)
$$
$$
y=rsin(inv\alpha)
$$
总结
渐开线是为了满足传动平稳运行正向构造出来的,线型可分解为圆切线处转动和平动的叠加。
依据这个原理其实我们可以构造很多齿廓曲线,比如我将基准圆改为带公转偏心圆,那么圆切线处运动分为公转+自转,这时候为了保证啮合,也可以构造平动方向的运动方程,这其实也是摆线齿轮的原理。
参考文献
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com