介绍
在纤维缠绕复合材料的设计合仿真中,筒身和封头段精准的壁厚是建立有限元网格模型的关键,没有准确的网格,就无法正确的计算出容器的应力和位移。
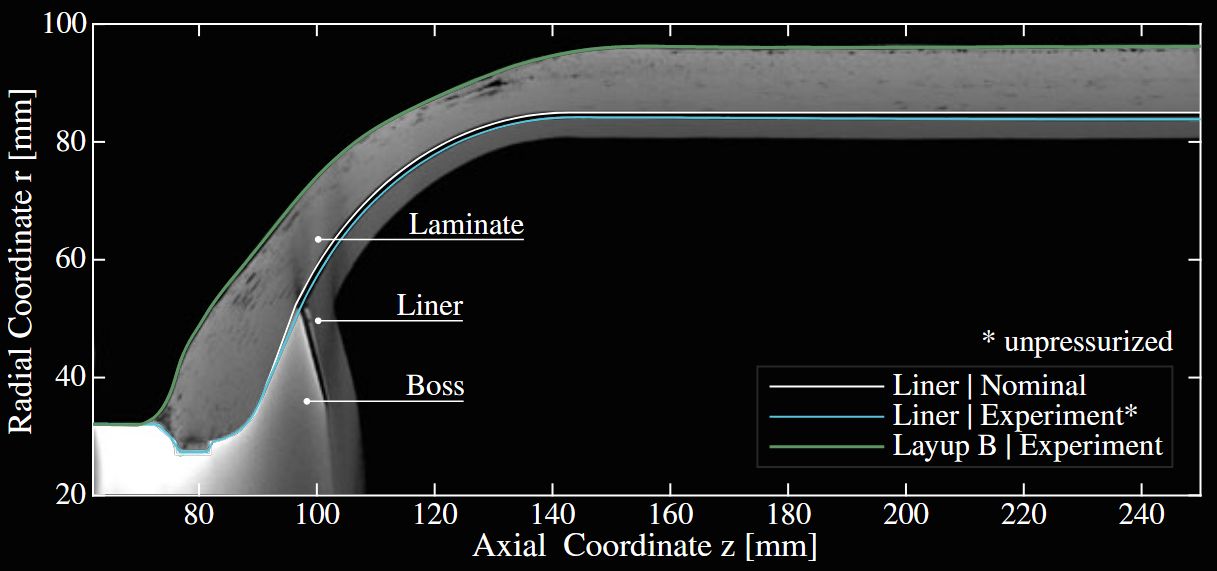
网格理论
对于厚度,最经典的公式是体积除以面积
$$
t=\frac{V}{A}
$$
在缠绕的过程中,纤维处于张紧的状态,可忽略截面积的变化。且暂时不考虑曲面表面曲率对纤维的影响。我们将缠绕芯模展开,把纤维投影到2D的平面中,对于一个固定的区间,为了保证芯模表面的均匀密布,每次纤维由下往上穿过区间,必然会有另一次由上往下经过区域。如果将表面划分为很多个区间,我们可以发现各个区间进出的次数是一致。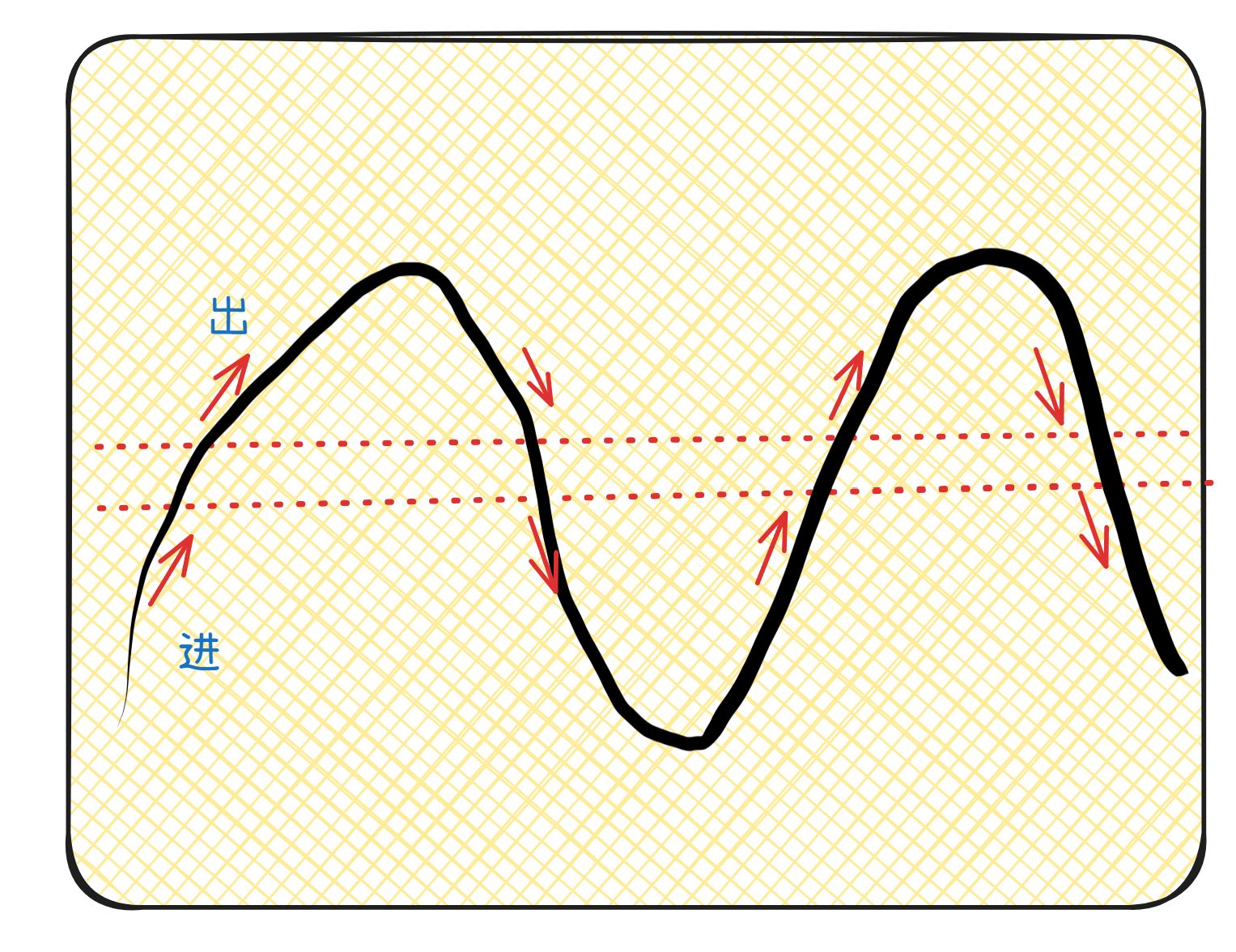
对于单次穿过,可以统计纤维的体积:
$$
Vi=h/cos(\theta)*A_f
$$
$A_f$是纤维的截面积,$\theta$为缠绕角,$h$为区域的高度。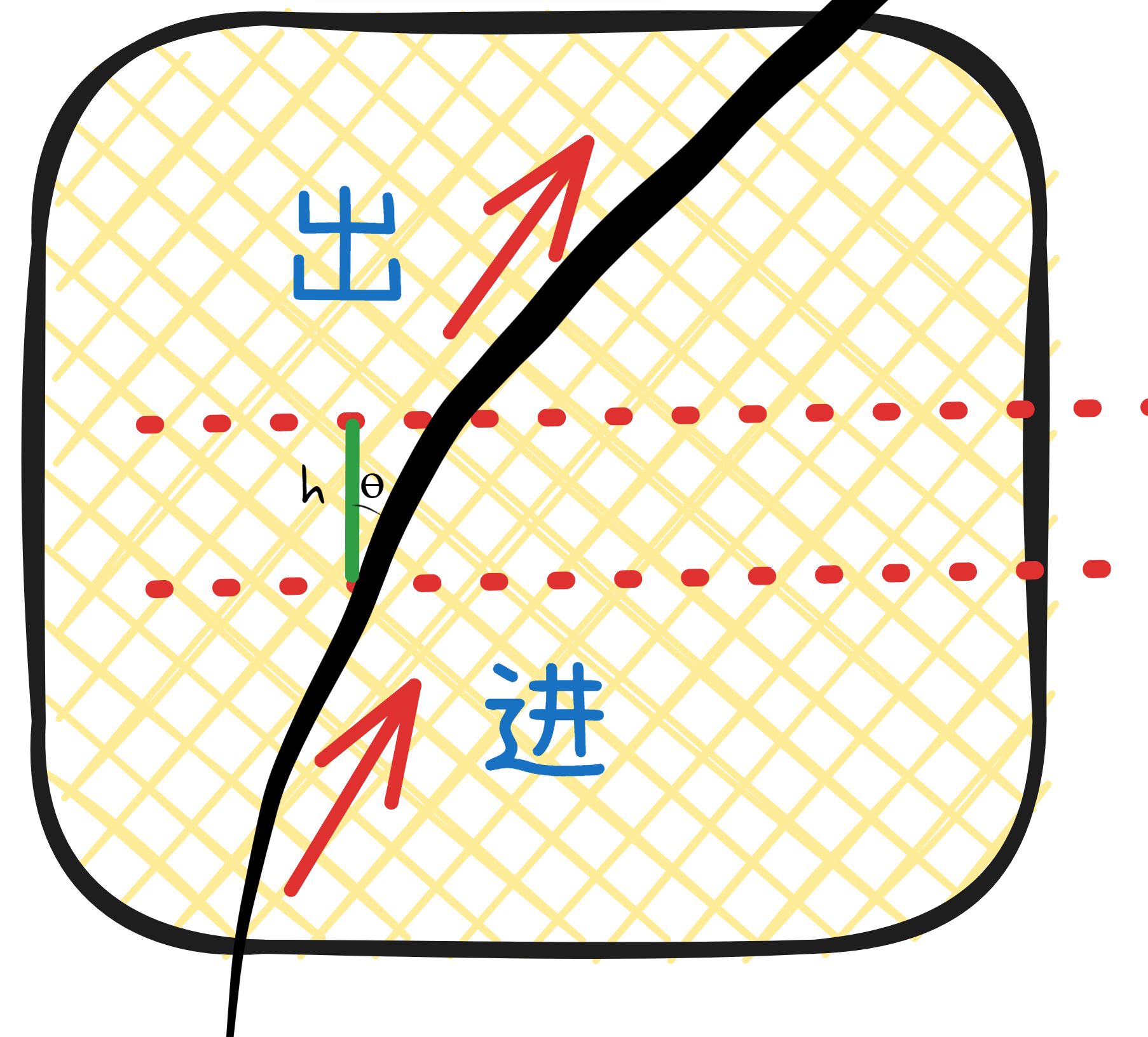
因为每次穿过该区间的缠绕角相同,穿过N次后,可算的总的体积为:
$$
V=Nh/cos(\theta)*A_f
$$
得到总体积后除以这个区间的表面积$2 \pi Rh$即可求得这个区间的纤维厚度:
$$
t=\frac{V}{A}=\frac{NA_f}{2 \pi Rcos(\theta)}
$$
通常纤维缠绕设计输入会指定初始位置处缠绕角$\alpha_0$,缠绕厚度$t_0$,我们根据初始位置处的半径$r_0$结合上式即可计算出芯模各个位置处的厚度
$$
t=t_0\frac{r_0cos(\alpha_0)}{rcos(\alpha)}
$$
90°区域处理
当某个区域的缠绕角为90°时,可以发现分母$rcos(\alpha)=0$,这样求解得到的厚度是无穷大,我们把90°的特殊情况绘制出来,可以发现纤维在这个地方积聚,这种情况通常发生在缠绕的边缘封头处,或者转接段处。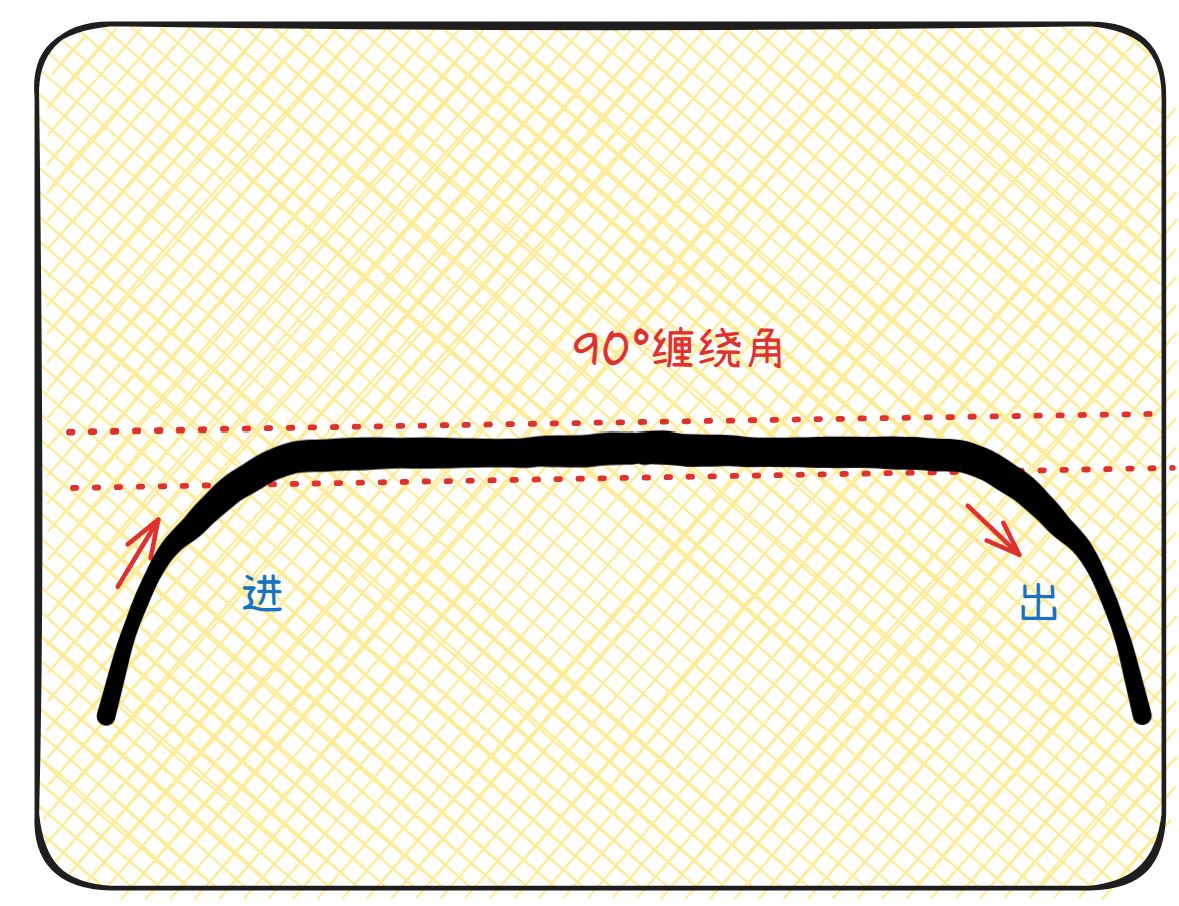
我们仍然用体积除以面积计算,此时需要统计单次进入该区域下转接段所旋转的角度$\beta$,在2D的平面图中为线段的长度。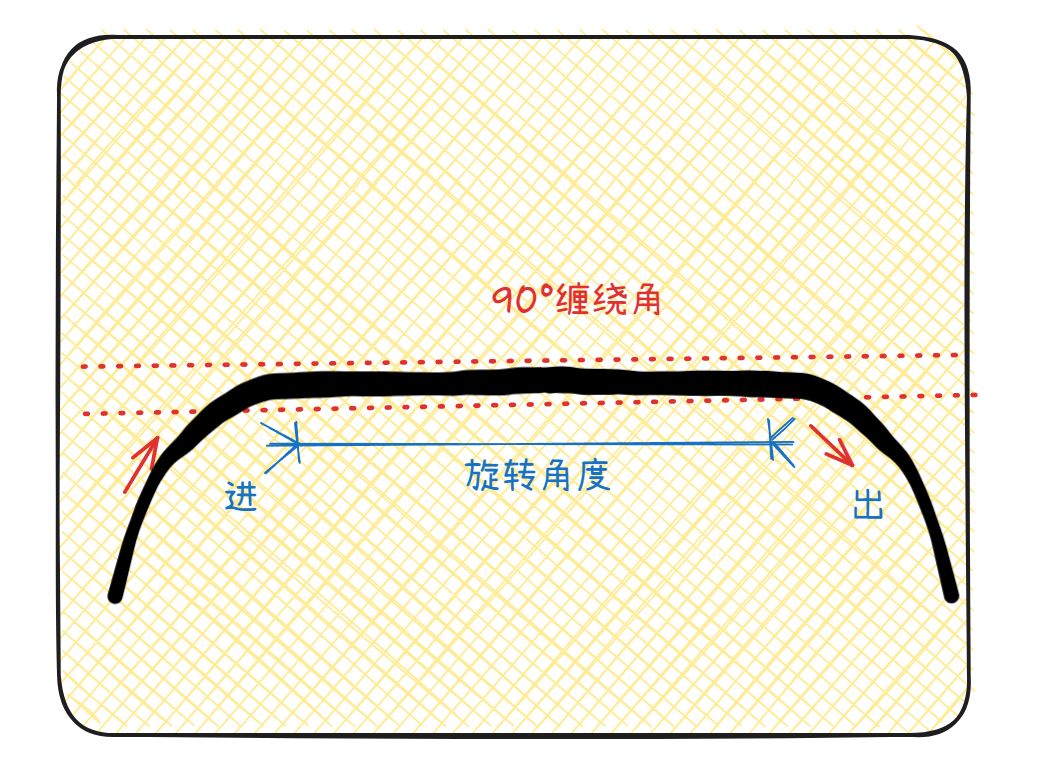
带入体积除以面的公式可得:
$$
t=\frac{V}{A}=\frac{N A_f \beta R}{2 \pi R h}=\frac{N A_f \beta }{2 \pi h}
$$
注意上式中依然存在着微分的小量h, 此时需要引入一些数学方法,比如龙格库塔法来求解。
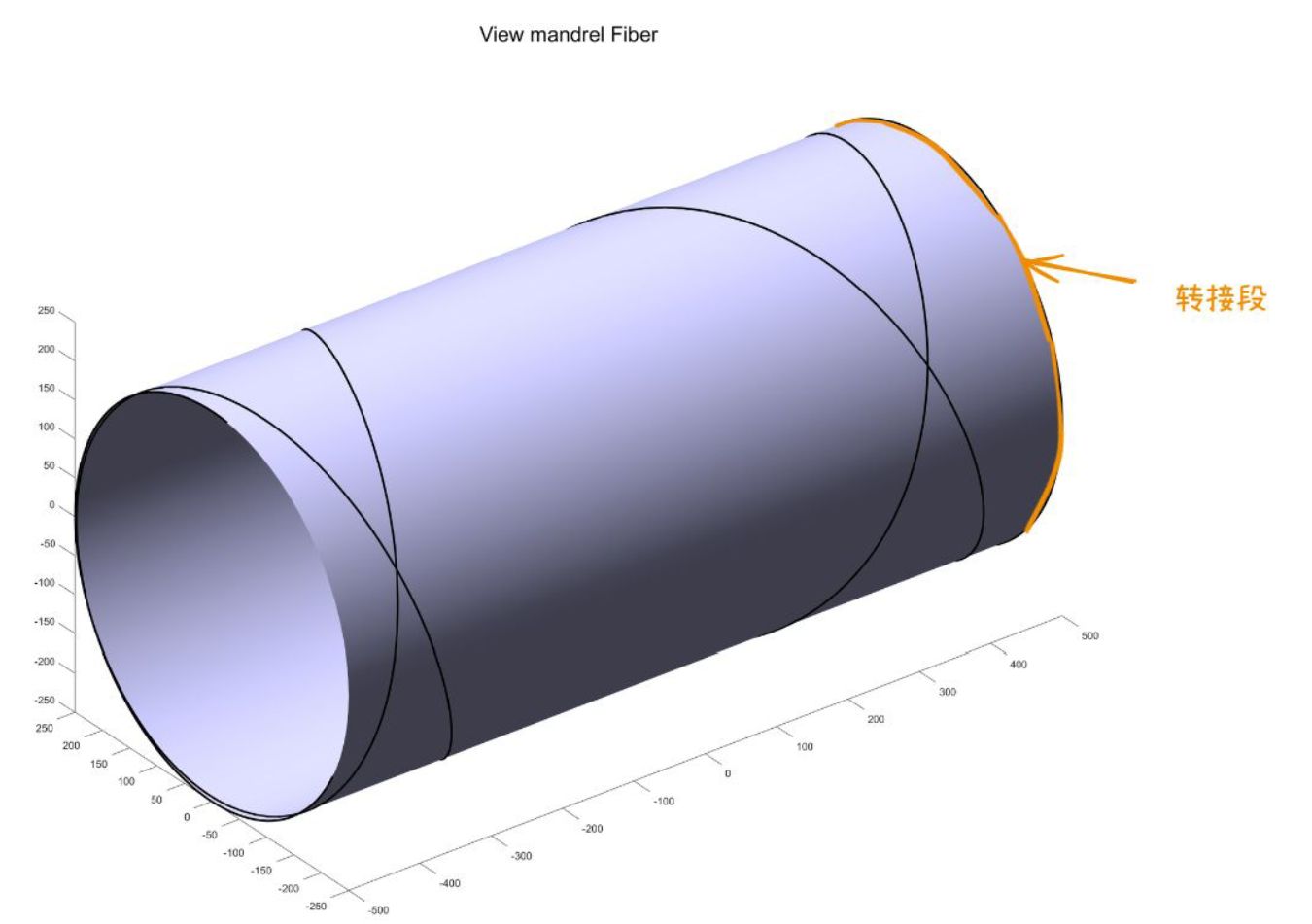
相比较于市面上纤维缠绕教材中的公式,本文的90°缠绕的公式中新引入了转接段转过角度的影响,考虑的东西会更加全面,也更贴近于实际。
参考文献
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com