介绍
Bearing_Dynamic用来简单计算轴承的缺陷频率。
原理
令参数$\gamma$为
$$
\gamma=\frac{D_w}{D_{pw}}cos(\alpha)
$$
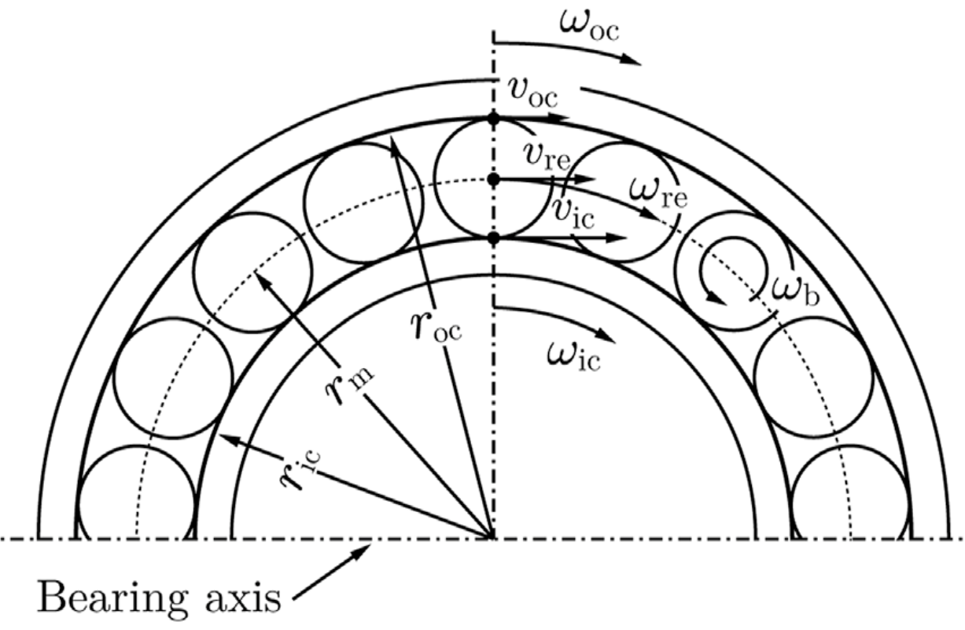
内圈角速度为:
$$
v_i=\frac{\pi n_i D_{pw}}{60}(1-\gamma)
$$
外圈角速度为:
$$
v_o=\frac{\pi n_i D_{pw}}{60}(1+\gamma)
$$
保持架转速为:
$$
n_m=\frac{1}{2}[n_i(1-\gamma)+n_o(1+\gamma)]
$$
滚动体的转速为:
$$
n_R=\frac{D_{pw}}{2D_w}(n_o-n_i)
$$
类结构
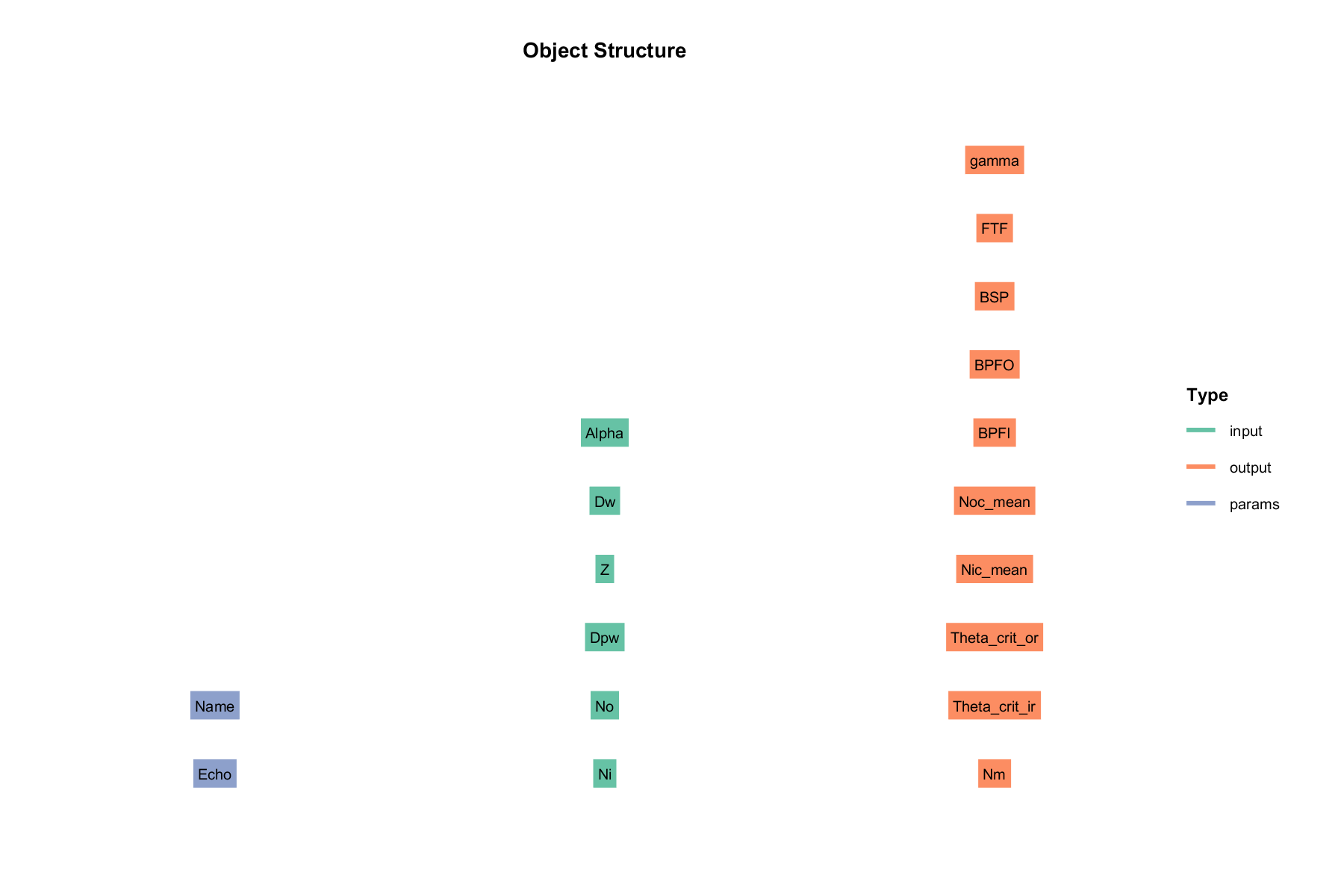
输入 input:
- Alpha : 接触角 [°]
- Dw : 滚子或球直径 [mm]
- Z : 滚子数量
- Dpw : 轴承分度圆直径 [mm]
- Ni : 内圈转速 [RPM]
- No : 外圈转速 [RPM]
参数 params:
- Name : 名称
输出 output :
- gamma : 参数
- FTF : 保持架缺陷频率 [Hz]
- BSP : 滚动体缺陷频率 [Hz]
- BPFO : 外圈缺陷频率 [Hz]
- BPFI : 内圈缺陷频率 [Hz]
- Noc_mean : 外圈旋转一圈的平均接触次数
- Nic_mean : 内圈旋转一圈的平均接触次数
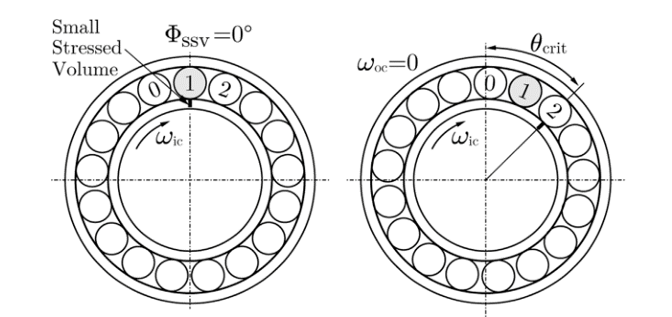
- Theta_crit_ir : 内圈两次接触间隔角度 [°]
- Theta_crit_or’ : 外圈两次接触间隔角度 [°]
案例
Demo (Flag=1)
inputStruct1.Ni=585; % RPM
inputStruct1.No=-15; % RPM
inputStruct1.Z=14;
inputStruct1.Dw=5; % mm
inputStruct1.Dpw=31; % mm
inputStruct1.Alpha=0; % °
paramsStruct1=struct();
B= bearing.Bearing_Dynamic(paramsStruct1, inputStruct1);
B= B.solve();
disp(B.output)
Nm: 236.6129
Theta_crit_ir: 43.1786
Theta_crit_or: 1.5330
Nic_mean: 8.3375
Noc_mean: 234.8387
BPFI: 81.2903
BPFO: 58.7097
BSP: 30.1935
FTF: 24.7780
gamma: 0.1613
参考文献
本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com