SignalAnalysis - 信号处理分析组件

Baffalo部件 Baffalo_Component 信号处理频谱分析

发布时间 : 2026-02-19 00:00

SignalAnalysis

Claude

介绍

SignalAnalysis 是用于信号处理分析的基础组件类。该类继承自 Component 框架，提供时间序列信号的处理和分析功能，包括时间间隔验证、信号变换、频谱分析、相关性分析和功率谱分析等功能。

原理

SignalAnalysis 基于 MATLAB 信号处理工具箱实现各种信号分析功能：

时间序列验证 - 验证输入时间序列的时间间隔是否均匀，计算采样间隔 dt
信号变换 - 支持小波变换、希尔伯特变换、快速傅里叶变换等
时频分析 - 支持同步挤压变换(SST)、瞬态提取变换(TET)、小波变换(WT)、Gabor 变换
相关性分析 - 自相关和互相关分析
功率谱分析 - 自功率谱密度(PSD)和互功率谱密度(CPSD)分析
信号滤波 - 信号平滑、巴特沃斯滤波、高斯低通滤波

类结构

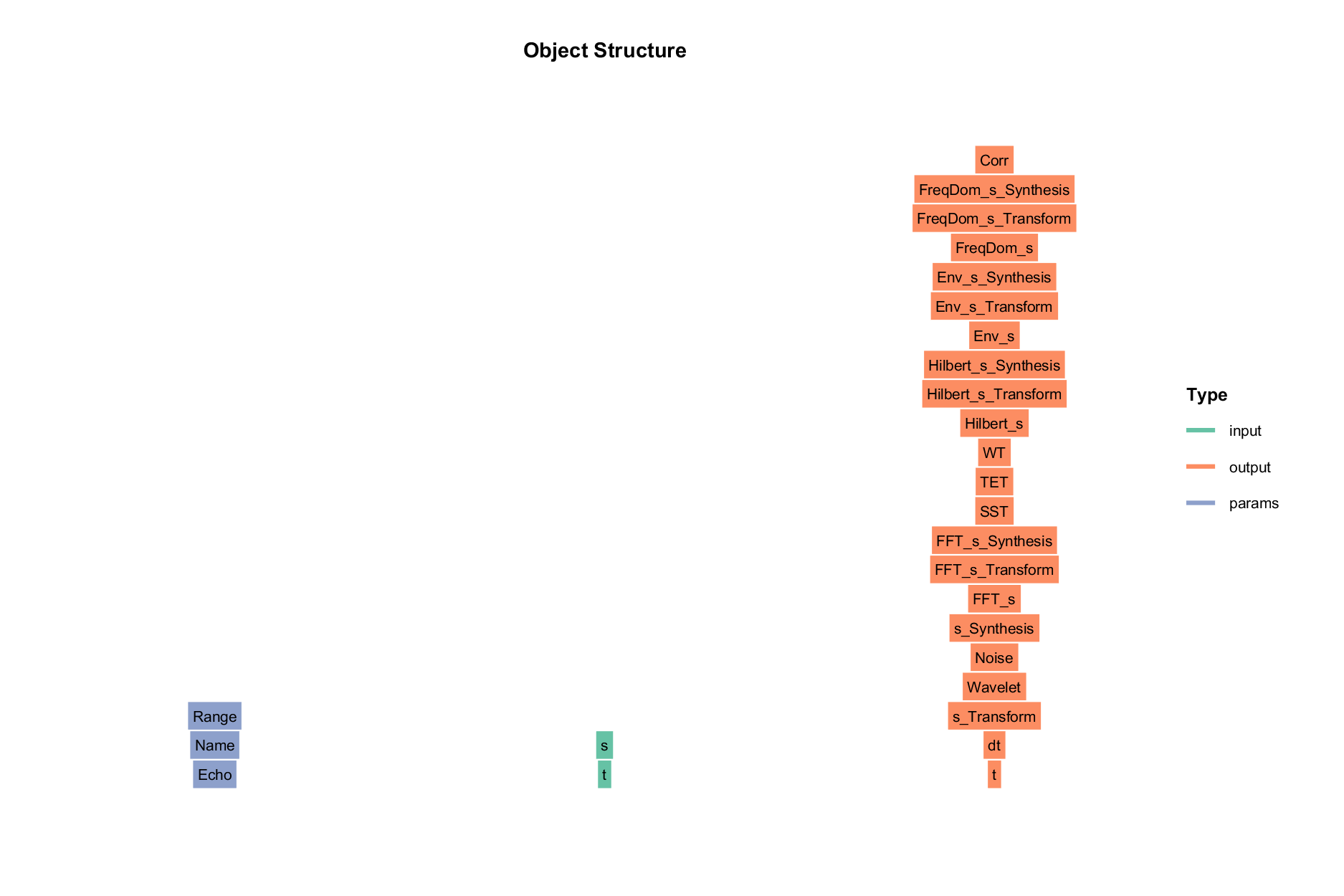
==输入 input:==

t : 时间数组 [s]
s : 信号幅值数组

==参数 params:==

Name : 组件名称 (默认 ‘SignalAnalysis_1’)
Range : 时间范围 [t1, t2]，默认为全部范围
Echo : 是否打印输出 (默认 1)

==输出 output :==

t : 输出时间数组
dt : 时间间隔 [s]
s_Transform : 变换后的信号
Wavelet : 小波
Noise : 噪声
s_Synthesis : 合成噪声后的信号
FFT_s : 原始信号快速傅里叶变换
FFT_s_Transform : 变换信号快速傅里叶变换
FFT_s_Synthesis : 合成信号快速傅里叶变换
SST : 同步挤压变换结果
TET : 瞬态提取变换结果
WT : 小波变换结果
Hilbert_s : 原始信号希尔伯特变换
Hilbert_s_Transform : 变换信号希尔伯特变换
Hilbert_s_Synthesis : 合成信号希尔伯特变换
Env_s : 原始信号包络
Env_s_Transform : 变换信号包络
Env_s_Synthesis : 合成信号包络
FreqDom_s : 原始信号主频
FreqDom_s_Transform : 变换信号主频
FreqDom_s_Synthesis : 合成信号主频
Corr : 相关性分析结果

==基准 Baseline：==

无

==安全裕度 Capacity :==

无

案例

Demo1 - 正弦波信号测试

案例介绍：

生成包含两个频率成分的正弦波信号（50Hz + 150Hz），验证时间间隔计算功能。

图表：

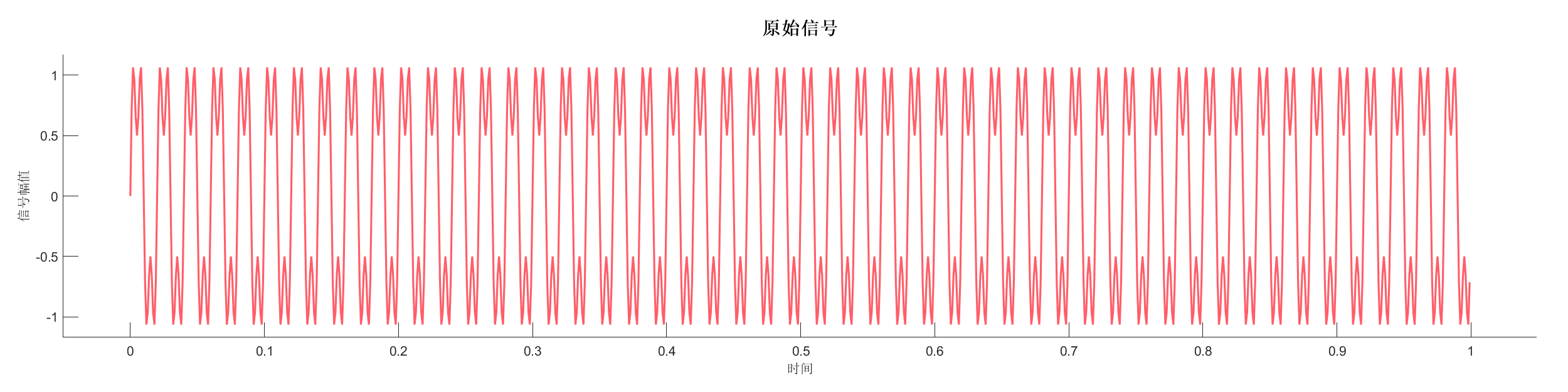
源代码：

% 生成测试数据
fs = 1000;  % 采样频率
T = 1;      % 信号时长 [s]
t = 0:1/fs:T-1/fs;  % 时间数组
s = sin(2*pi*50*t) + 0.5*sin(2*pi*150*t);  % 信号幅值

% 输入结构
inputStruct.t = t;
inputStruct.s = s;

% 参数结构
paramsStruct.Name = 'SineWave_Signal';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();

% 打印信息
SA.PrintInfo();

% 绘制原始信号
PlotOriSignal(SA);

Demo2 - 叠加噪声的信号测试

案例介绍：

生成正弦波信号并叠加高斯白噪声，展示含噪信号的处理和分析。

图表：

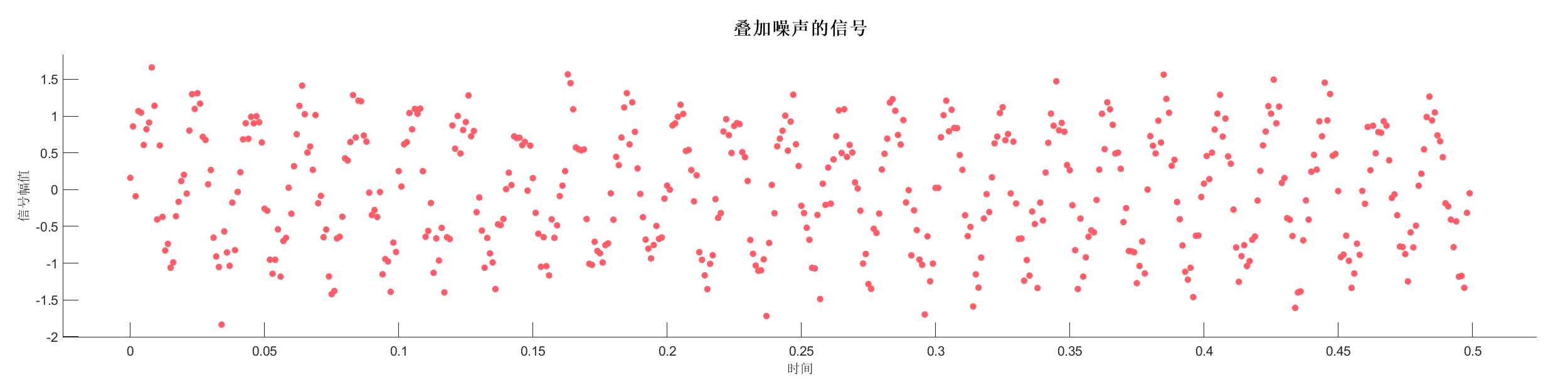
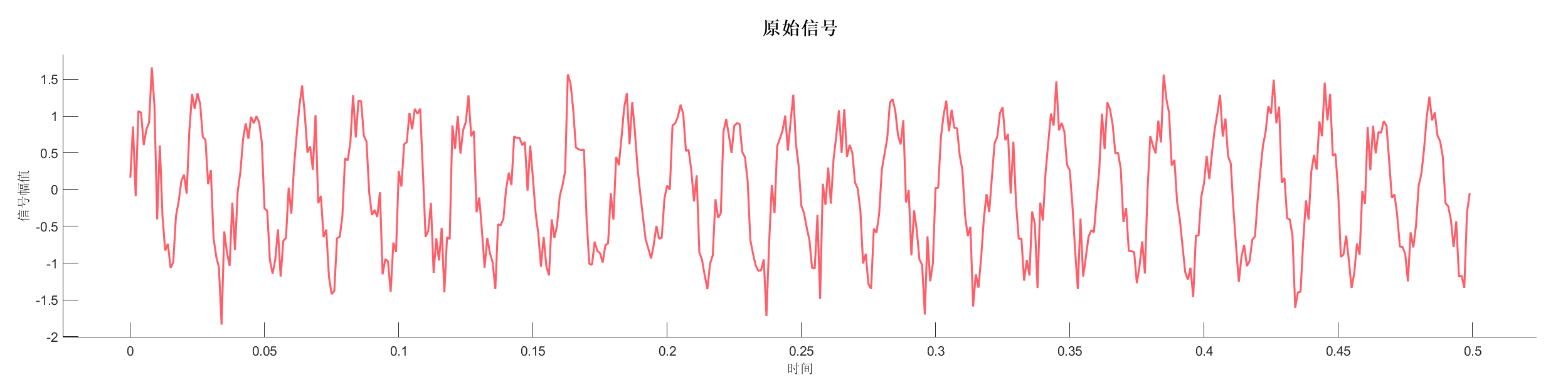
源代码：

% 生成测试数据
fs = 1000;  % 采样频率
T = 0.5;    % 信号时长 [s]
t = 0:1/fs:T-1/fs;  % 时间数组
s_clean = sin(2*pi*50*t);
noise = 0.3 * randn(size(t));
s = s_clean + noise;  % 叠加噪声

% 输入结构
inputStruct.t = t;
inputStruct.s = s;

% 参数结构
paramsStruct.Name = 'Noisy_Signal';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();

% 打印信息
SA.PrintInfo();

% 绘制原始信号
PlotOriSignal(SA);
PlotOriSignal(SA, 'Title', '叠加噪声的信号', 'Geom', 'point');

Demo3 - 自定义信号测试 (Ricker 小波)

案例介绍：

生成 Ricker 小波（墨西哥帽小波）信号，展示自定义信号的处理。

图表：

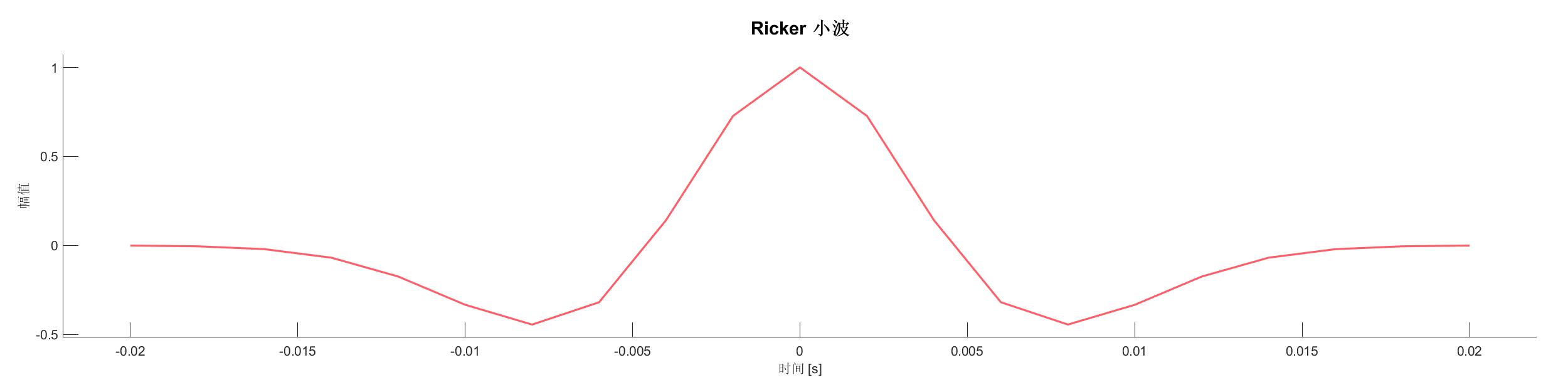
源代码：

% 生成测试数据 - Ricker 小波
fs = 500;   % 采样频率
t = -0.02:1/fs:0.02;  % 时间数组
f0 = 50;    % 主频
a = (pi * f0 * t).^2;
s = (1 - 2*a) .* exp(-a);  % Ricker 小波

% 输入结构
inputStruct.t = t;
inputStruct.s = s;

% 参数结构
paramsStruct.Name = 'RickerWavelet';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();

% 打印信息
SA.PrintInfo();

% 绘制原始信号
PlotOriSignal(SA, 'Title', 'Ricker 小波', 'XLabel', '时间 [s]', 'YLabel', '幅值', 'Geom', 'line');

Demo4 - 最小相位和零相位小波对比

案例介绍：

创建反射系数序列，使用不同相位类型的小波进行变换，对比最小相位和零相位小波的效果。

图表：

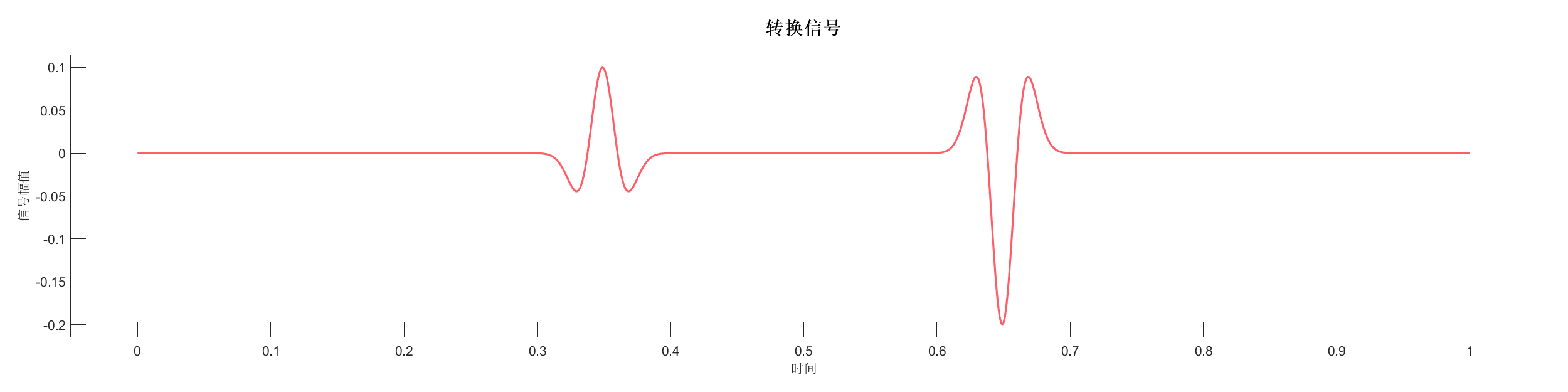
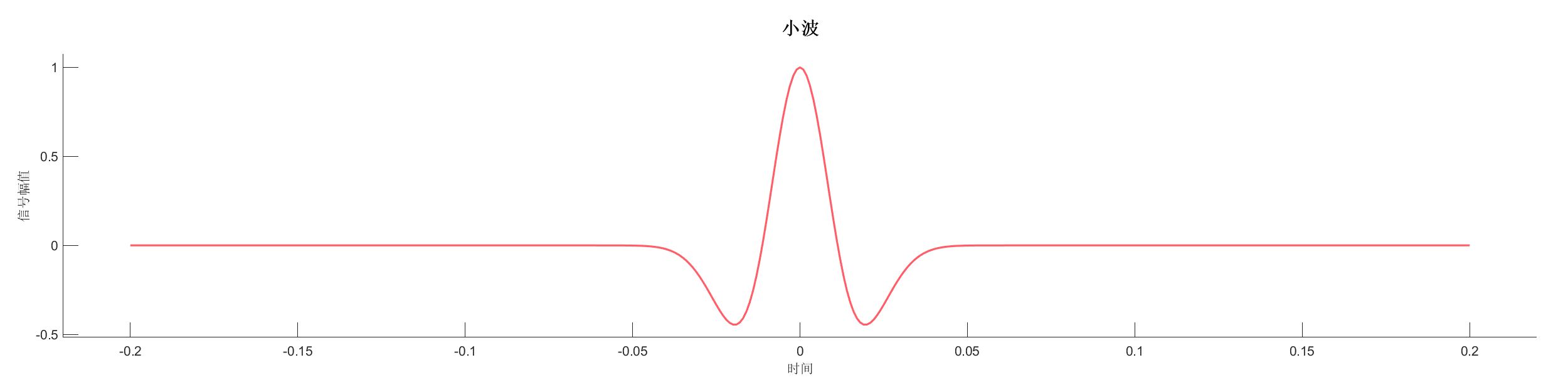
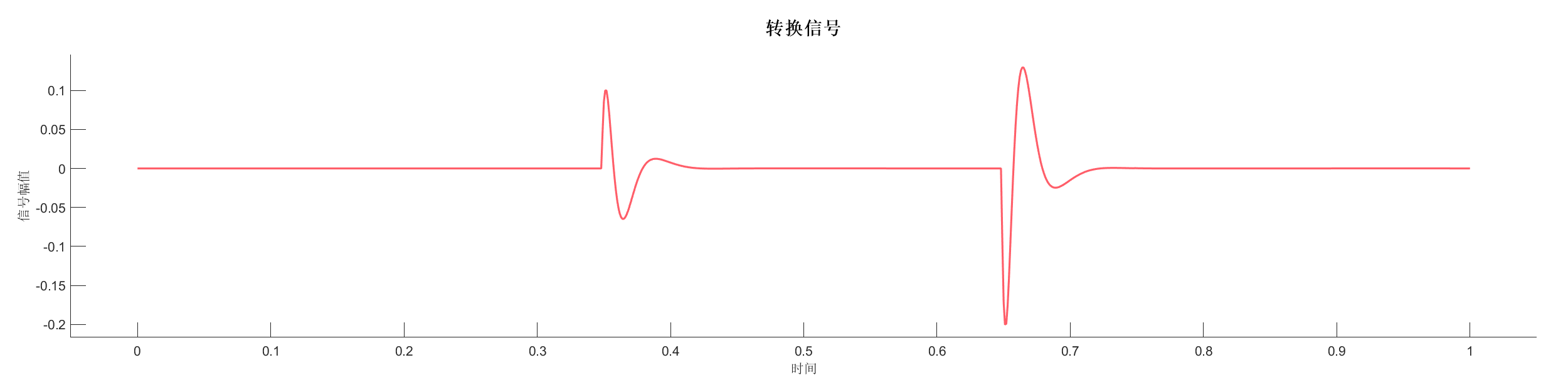
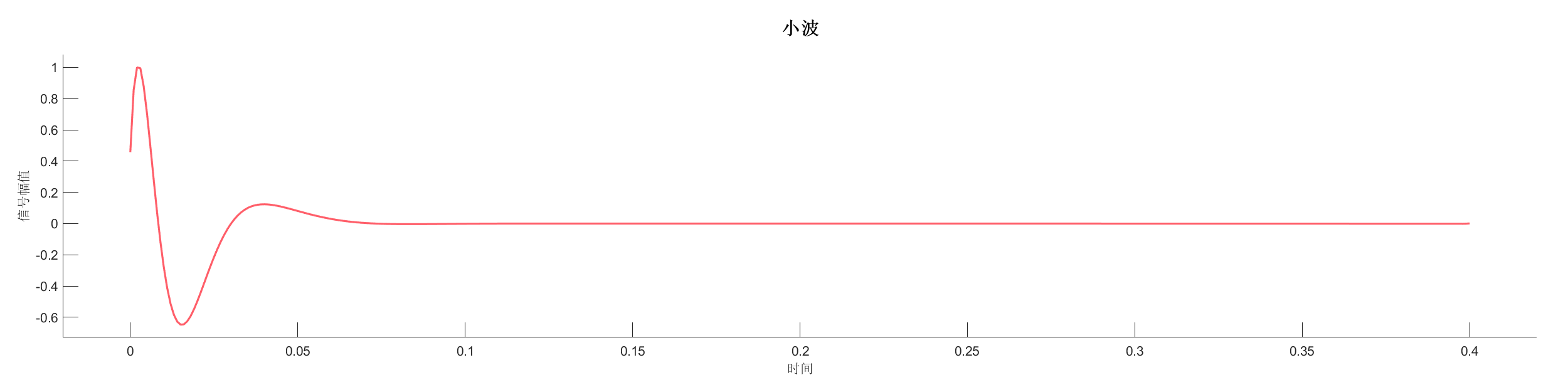
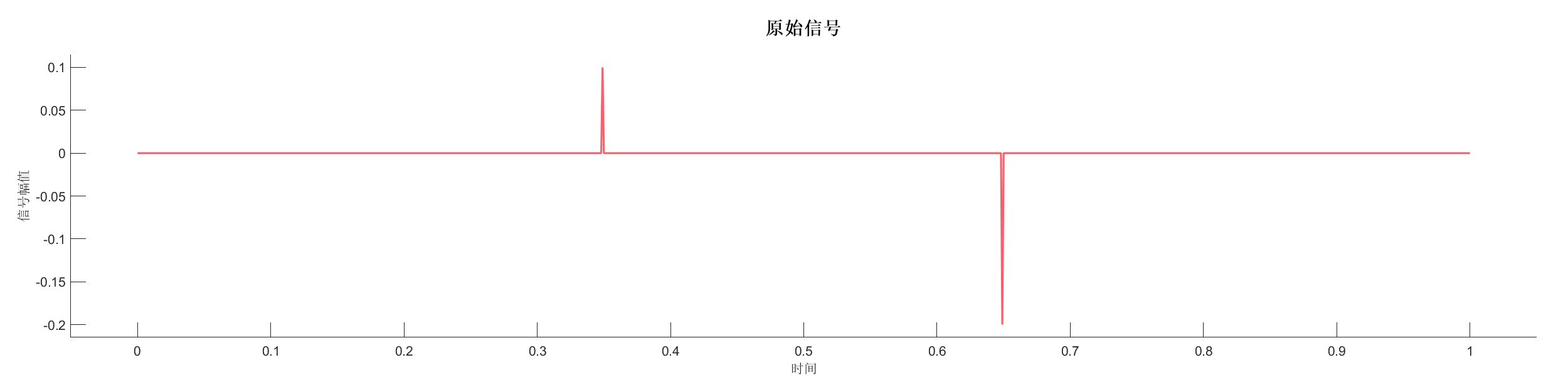
源代码：

% 创建反射系数序列
r = zeros(1001, 1);  % 创建长度为1001的零向量
r(350) = 0.1;            % 在位置350设置正反射系数
r(650) = -0.2;           % 在位置650设置负反射系数

% 时间参数
dt = 0.001;               % 时间采样间隔 [s]
t = (0:1000)*dt;         % 时间坐标向量 [s]

% 输入结构
inputStruct.t = t;
inputStruct.s = r;

% 参数结构
paramsStruct.Name = 'Demo4_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();
PlotOriSignal(SA);

SA = WaveletTransform(SA, 'WaveType','min','tlength',0.4,'fdom',20);
PlotWavelet(SA);
PlotTransformSignal(SA);

SA = WaveletTransform(SA, 'WaveType','zero','tlength',0.4,'fdom',20);
PlotWavelet(SA);
PlotTransformSignal(SA);

Demo5 - 添加随机噪声

案例介绍：

生成反射系数序列，使用最小相位小波变换后添加随机噪声，展示噪声对信号的影响。

图表：

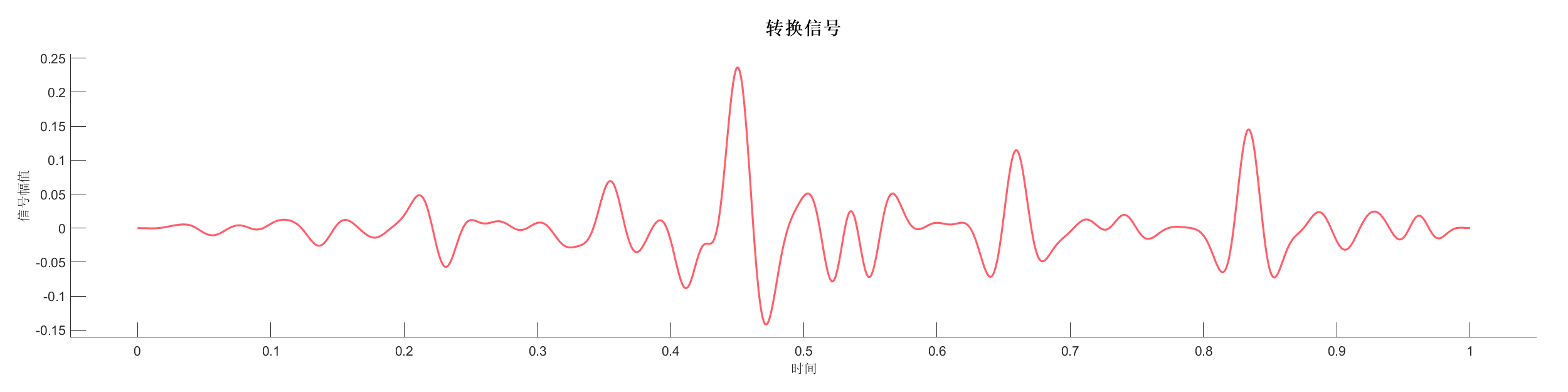
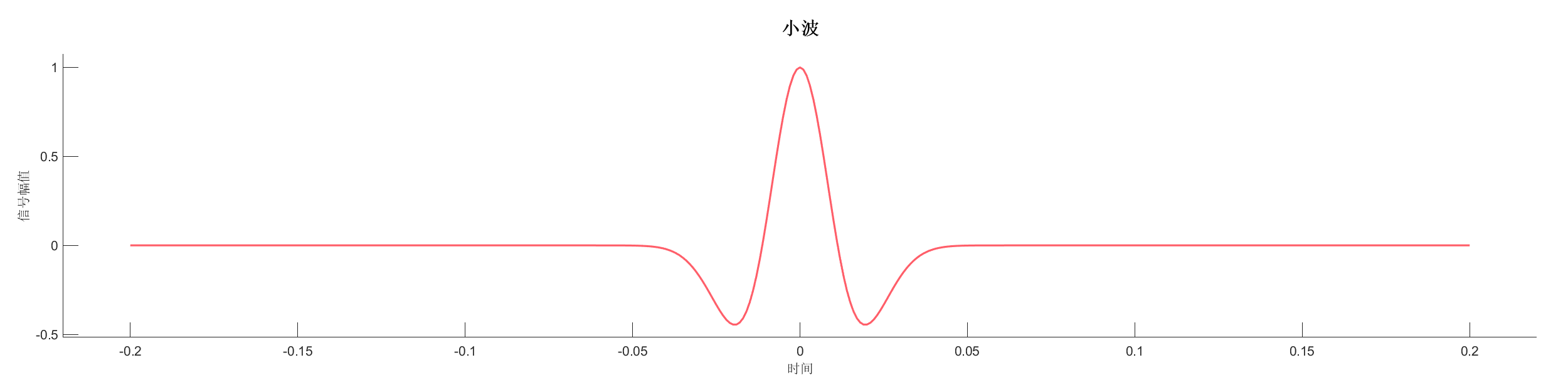
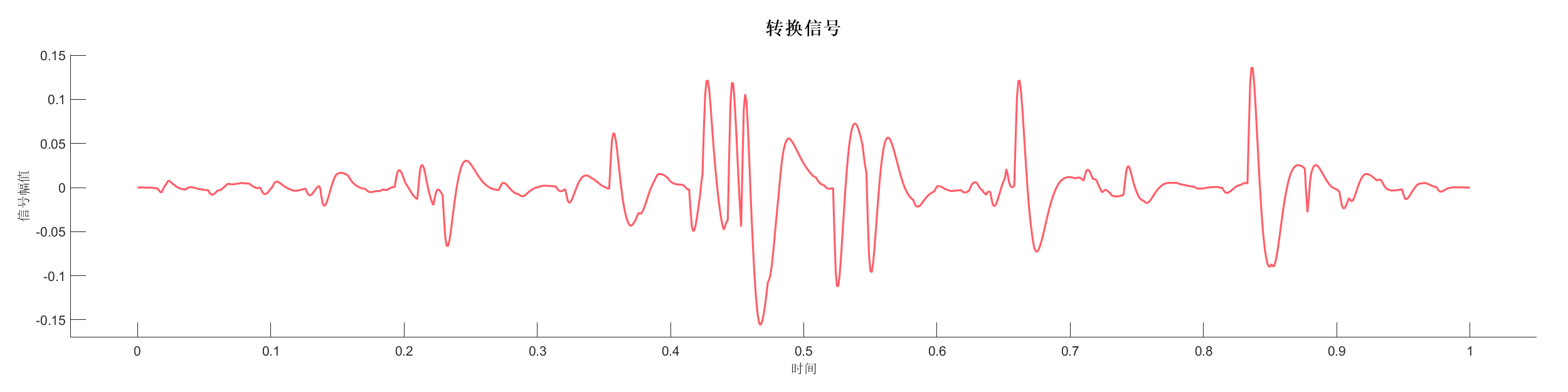
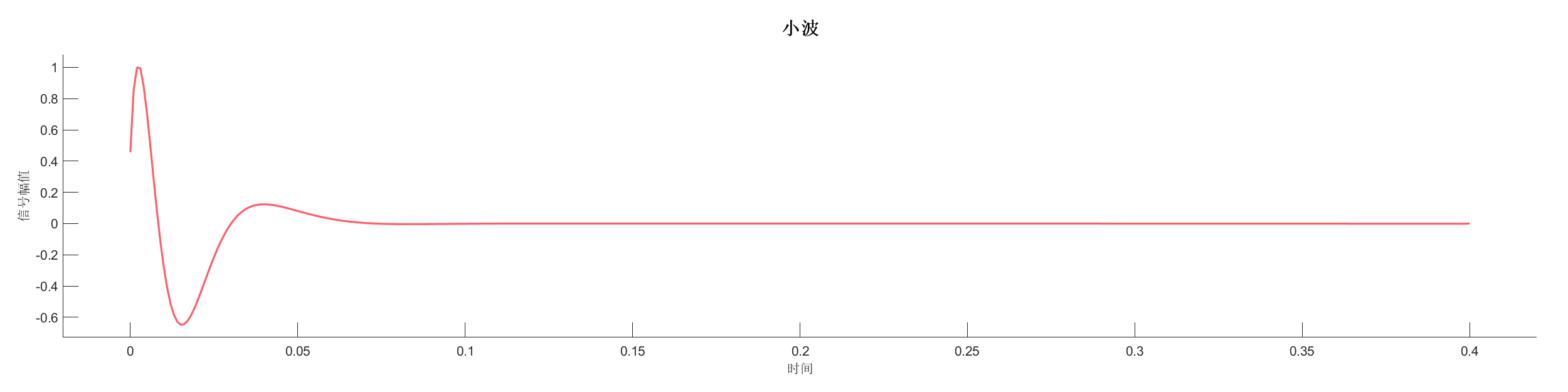
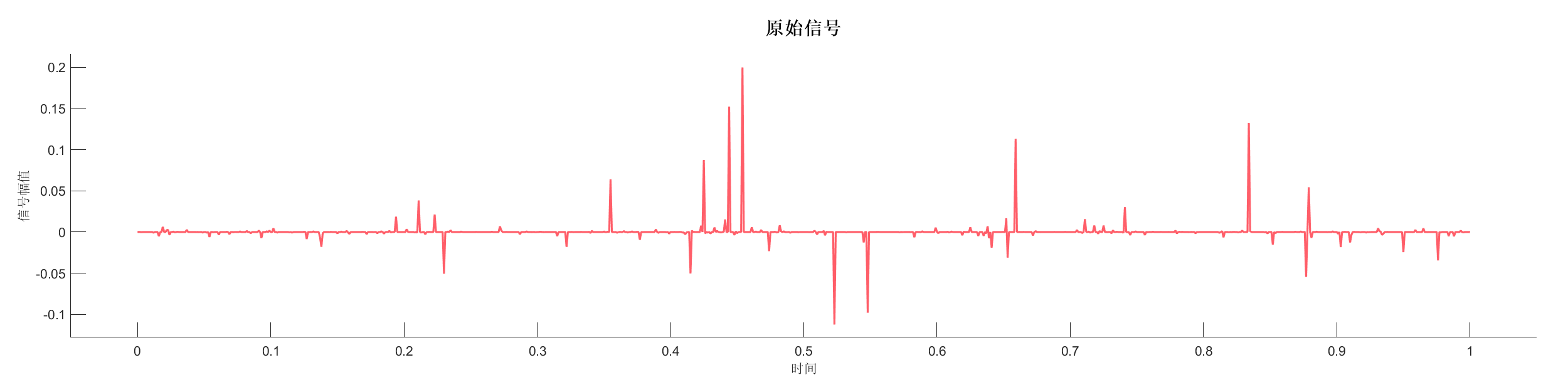
源代码：

dt = .001;  % time sample size
t = (0:1000)*dt;  % time coordinate vector
r = reflec(1, .001, .2, 7, 1);

% 输入结构
inputStruct.t = t;
inputStruct.s = r;

% 参数结构
paramsStruct.Name = 'Demo5_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();
PlotOriSignal(SA);

SA = WaveletTransform(SA, 'WaveType','min','tlength',0.4,'fdom',20);
PlotWavelet(SA);
PlotTransformSignal(SA);

SA = WaveletTransform(SA, 'WaveType','zero','tlength',0.4,'fdom',20);
PlotWavelet(SA);
PlotTransformSignal(SA);

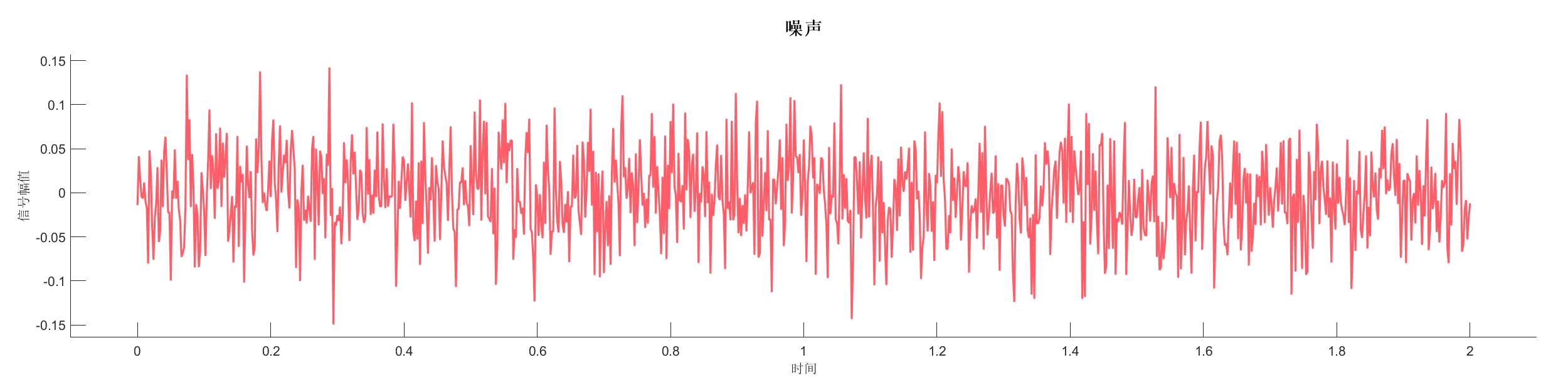
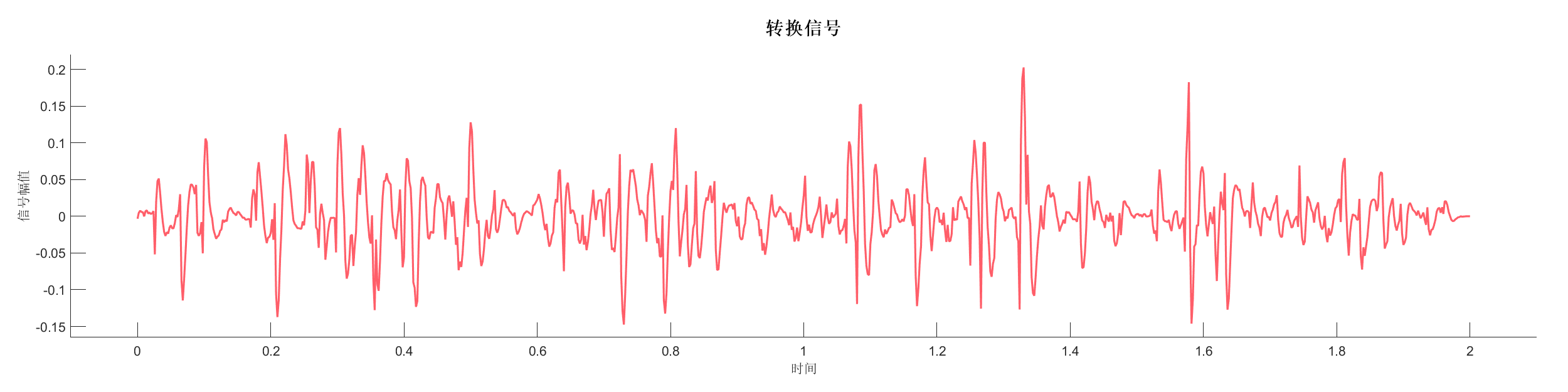
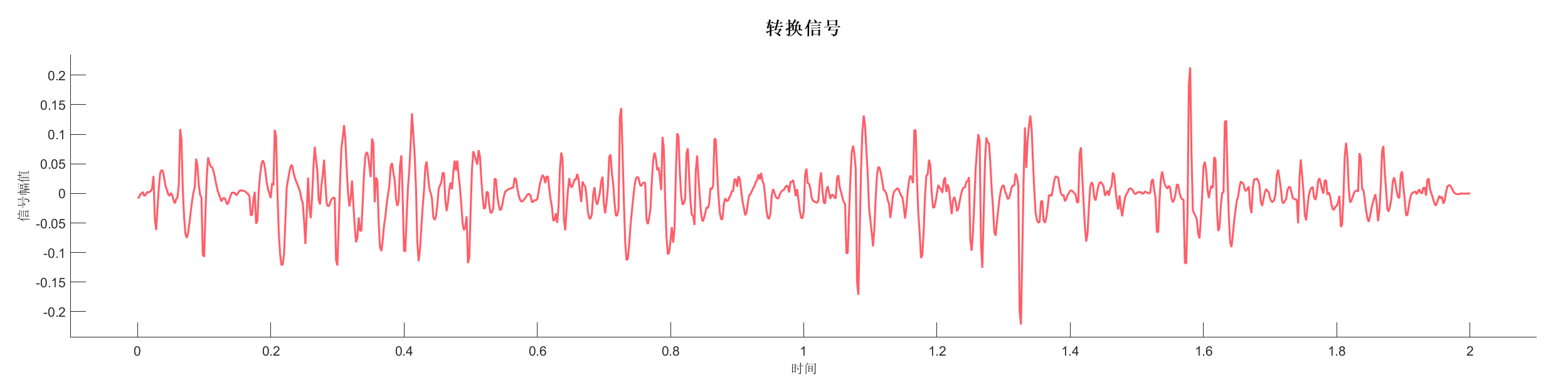
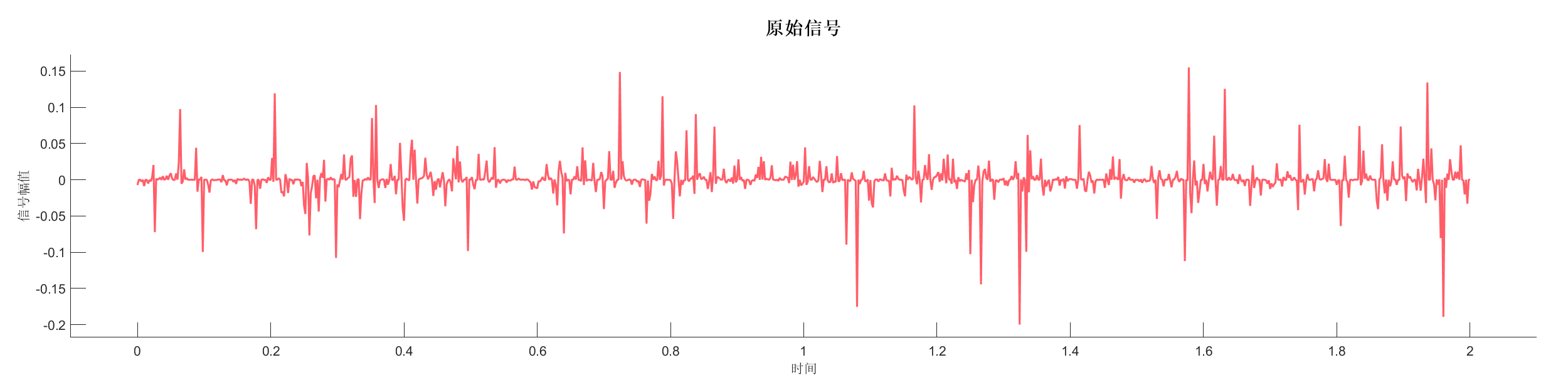
Demo6 - 相位旋转，加入噪声 (小波)

案例介绍：

创建包含两个反射系数序列的信号，添加相位旋转和随机噪声，展示相位变化对信号的影响。

图表：

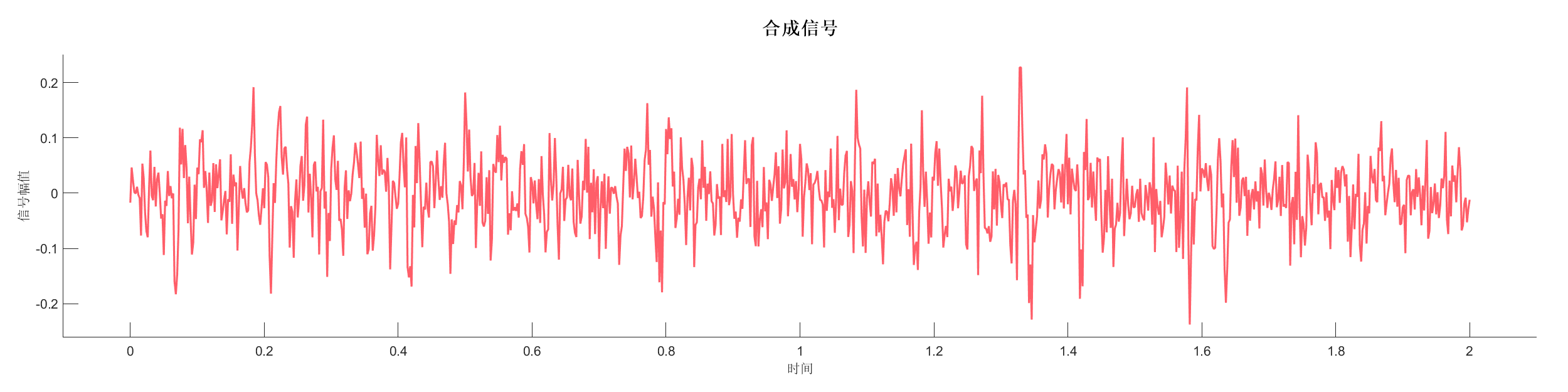
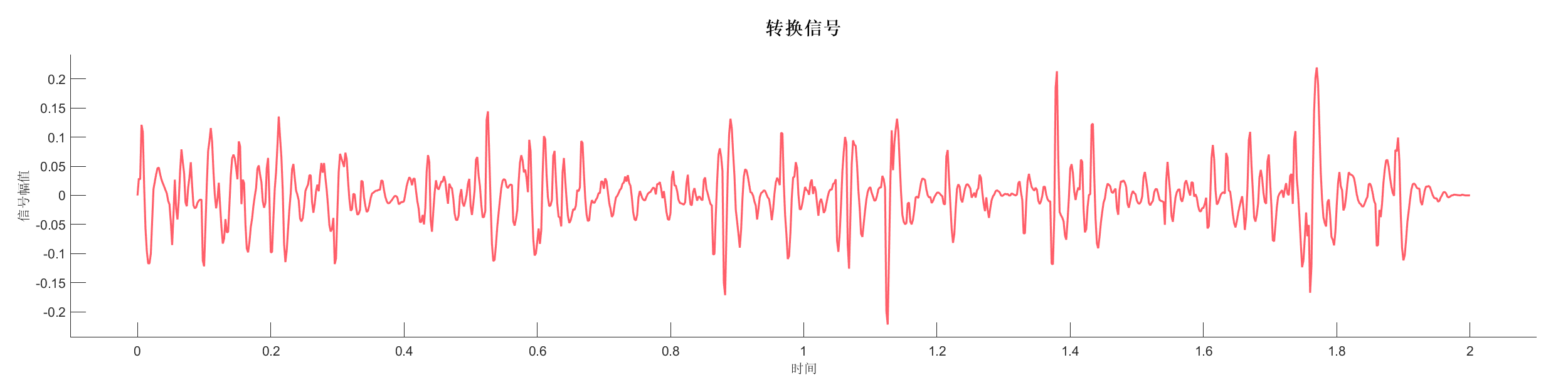
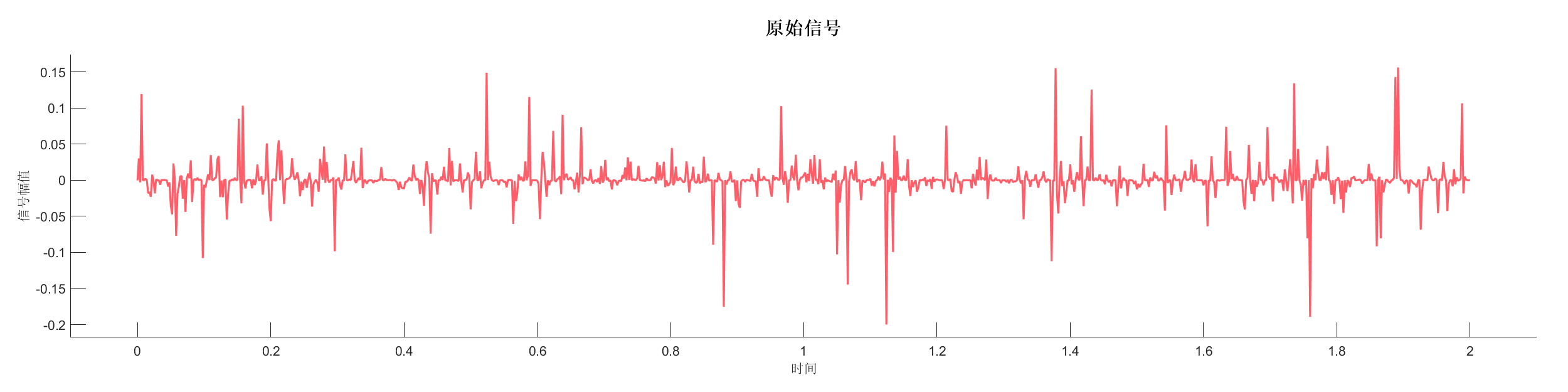
源代码：

dt = .002; tmax = 2;  % 时间采样间隔 [s] 和记录长度 [s]
fdom = 30; s2n = 1;  % 主频 [Hz] 和信噪比
nlag = 100;  % 第二个反射系的延迟样点数

% 创建反射系数序列
[r1, t] = reflec(tmax, dt, .2, 3, 5);  % 第一个反射系数序列
r2 = [zeros(nlag,1); r1(1:end-nlag)];  % r2 是 r1 延迟 nlag 个样本的结果
rtmp = reflec(2, dt, .2, 3, 9);  % 用于填充 r2 前部零值的临时反射系数
r2(1:nlag) = rtmp(1:nlag);  % 填充零值区域

% 输入结构
inputStruct.t = t;
inputStruct.s = r1;

% 参数结构
paramsStruct.Name = 'Demo6_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = WaveletTransform(SA1, 'WaveType','min','tlength',0.2,'fdom',fdom);
PlotTransformSignal(SA1);

inputStruct.s = r2;
paramsStruct.Name = 'Demo6_2';
SA2 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA2 = SA2.solve();
PlotOriSignal(SA2);

SA2 = WaveletTransform(SA2, 'WaveType','min','tlength',0.2,'fdom',fdom);
PlotTransformSignal(SA2);

SA2 = WaveletTransform(SA2, 'WaveType','min','tlength',0.2,'fdom',fdom,'phaserot',90);
PlotTransformSignal(SA2);

% 添加随机噪声
n1 = rnoise(SA1.output.s_Transform, s2n);  % 生成与 s1 信噪比为 s2n 的噪声
SA2 = AddNoise(SA2, n1);
PlotNoise(SA2);
PlotSyntheticSignal(SA2);

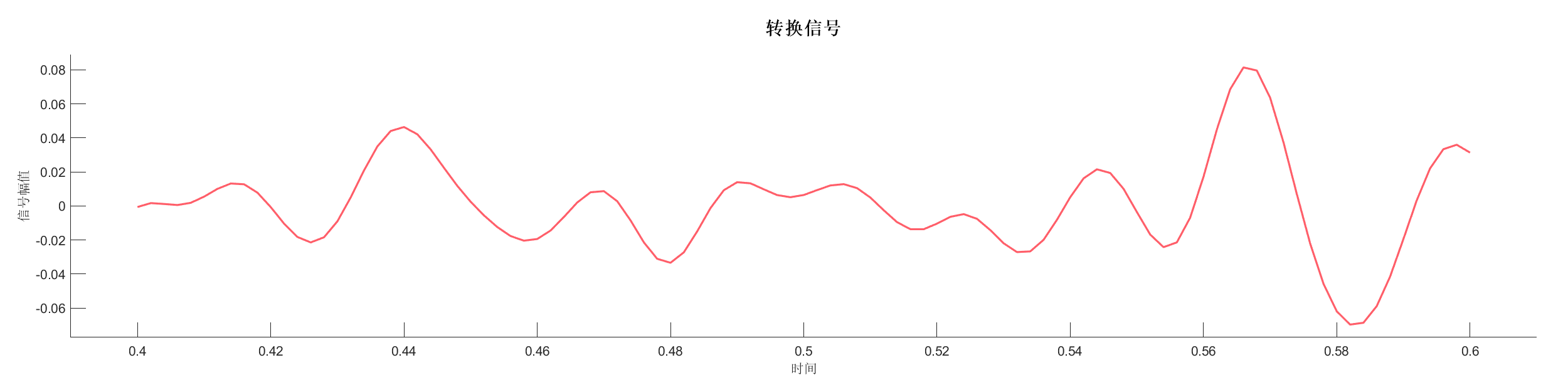
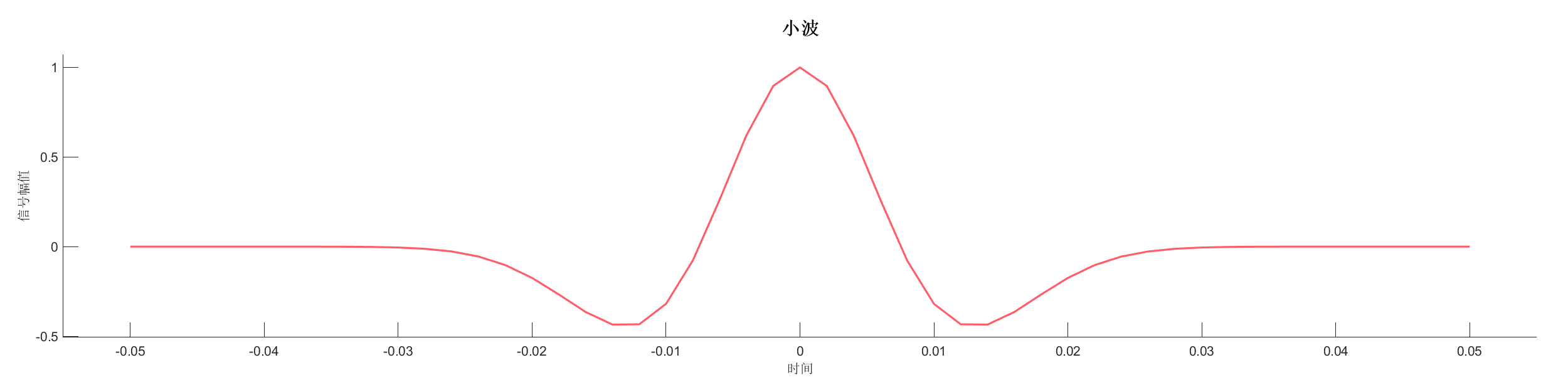
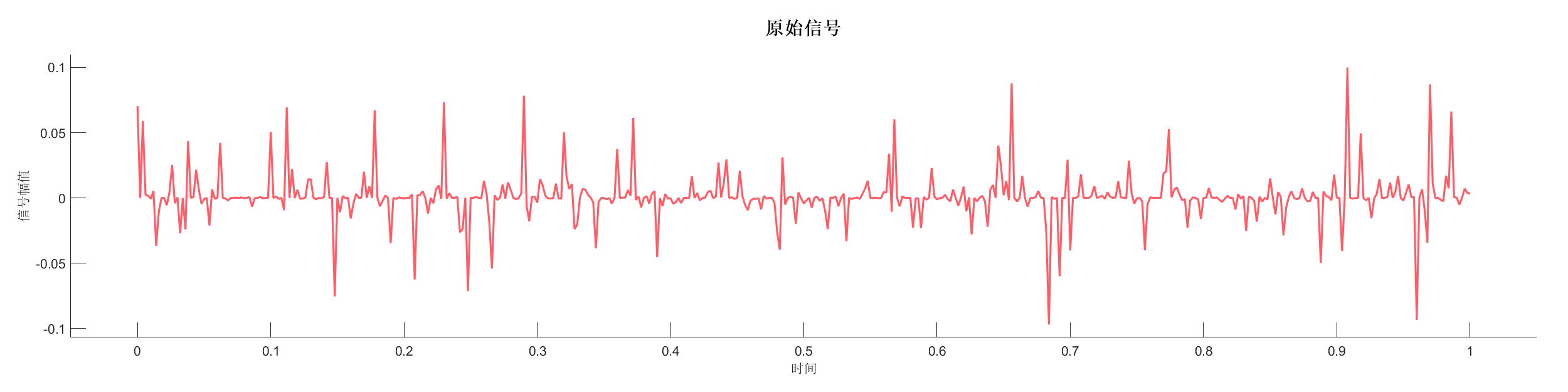
Demo7 - 时间偏移 (小波)

案例介绍：

创建反射系数序列，使用零相位小波变换并应用时间偏移，展示时间偏移对信号的影响。

图表：

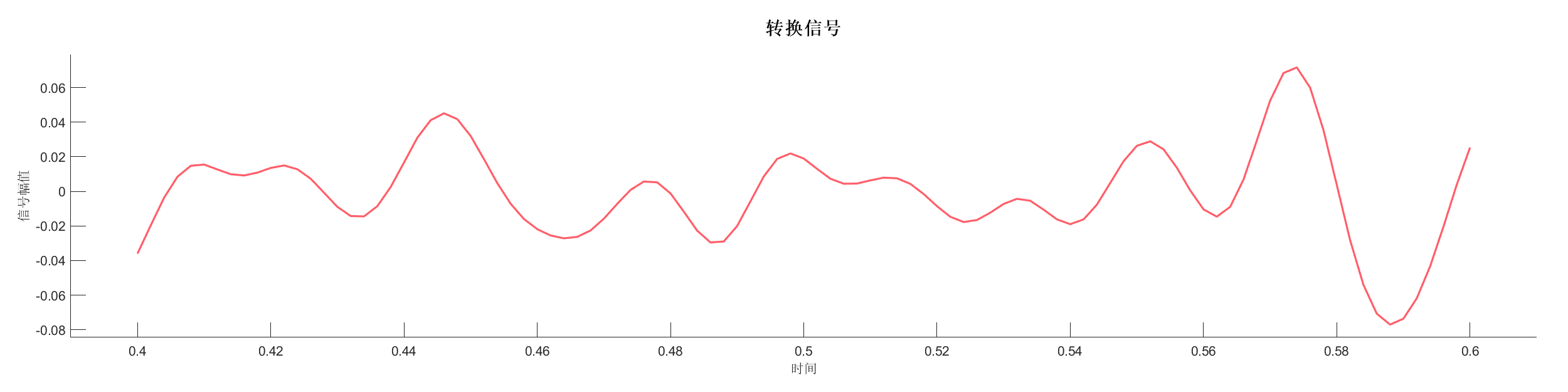
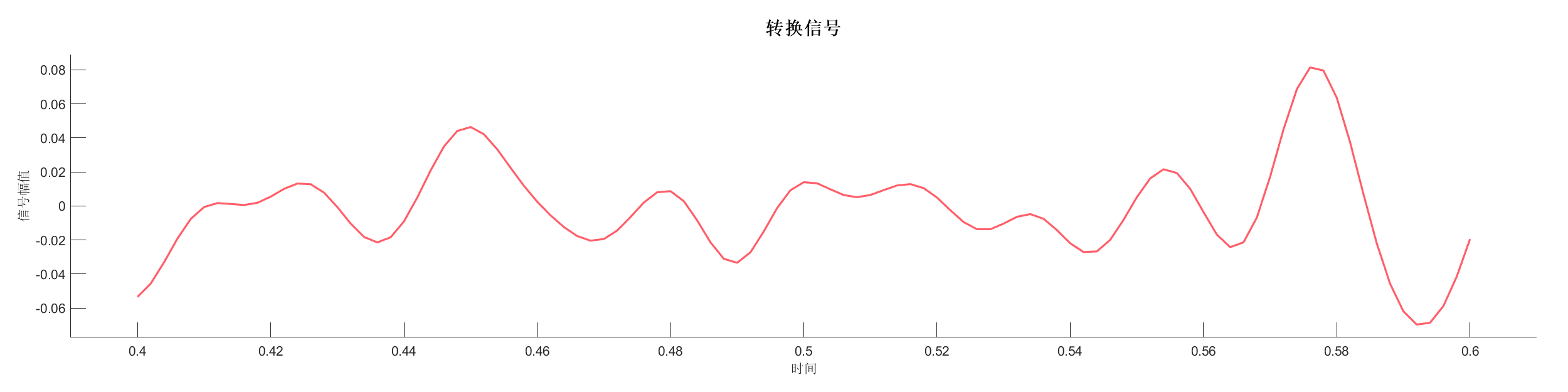
源代码：

dt = .002;
tmax = 1;
tlen = .1;
t1 = .4; t2 = .6;
[r, tr] = reflec(tmax, dt, .1, 3, 4);
fdom = 30;

% 输入结构
inputStruct.t = tr;
inputStruct.s = r;

% 参数结构
paramsStruct.Name = 'Demo7_1';
paramsStruct.Range = [t1, t2];
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = WaveletTransform(SA1, 'WaveType','zero','tlength',tlen,'fdom',fdom);
PlotWavelet(SA1);
PlotTransformSignal(SA1);

SA1 = WaveletTransform(SA1, 'WaveType','zero','tlength',tlen,'fdom',fdom,'shift',0.01);
PlotTransformSignal(SA1);

SA1 = WaveletTransform(SA1, 'WaveType','zero','tlength',tlen,'fdom',fdom,'shift',0.01,'phaserot',45);
PlotTransformSignal(SA1);

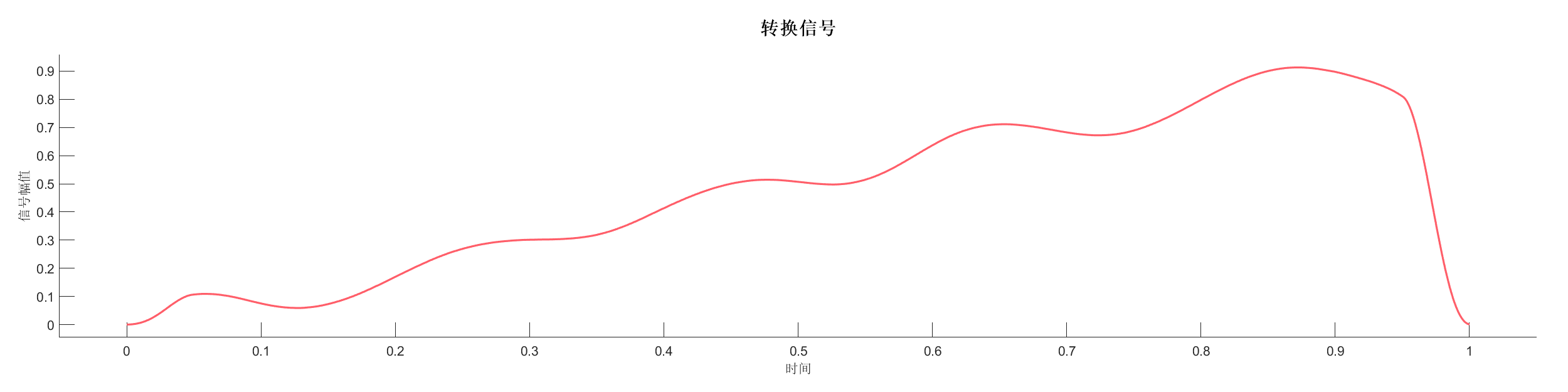
Demo8 - 信号平滑 (小波)

案例介绍：

创建包含低频正弦波和线性趋势的信号，添加随机噪声后使用不同方法进行平滑处理。

图表：

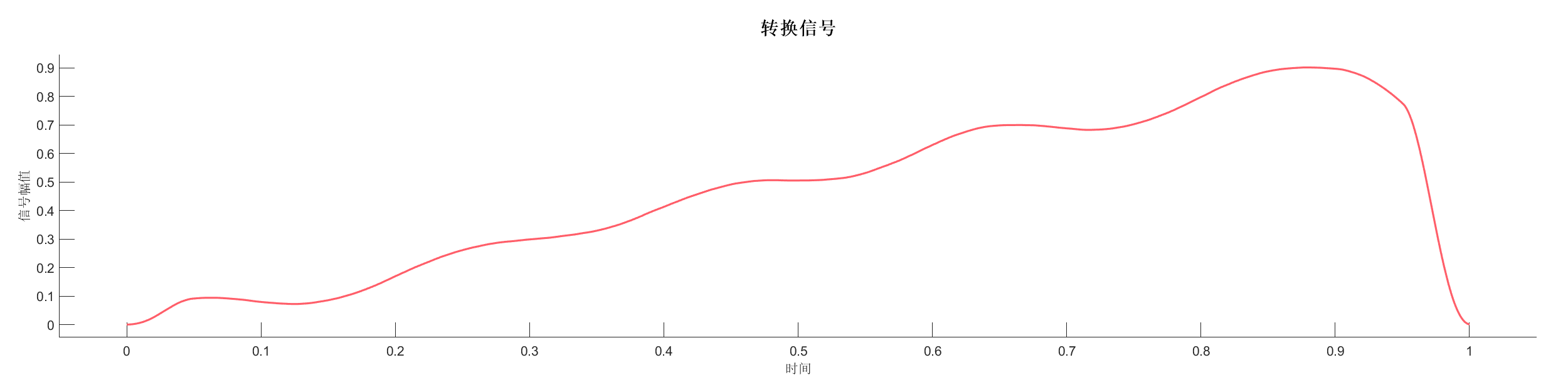
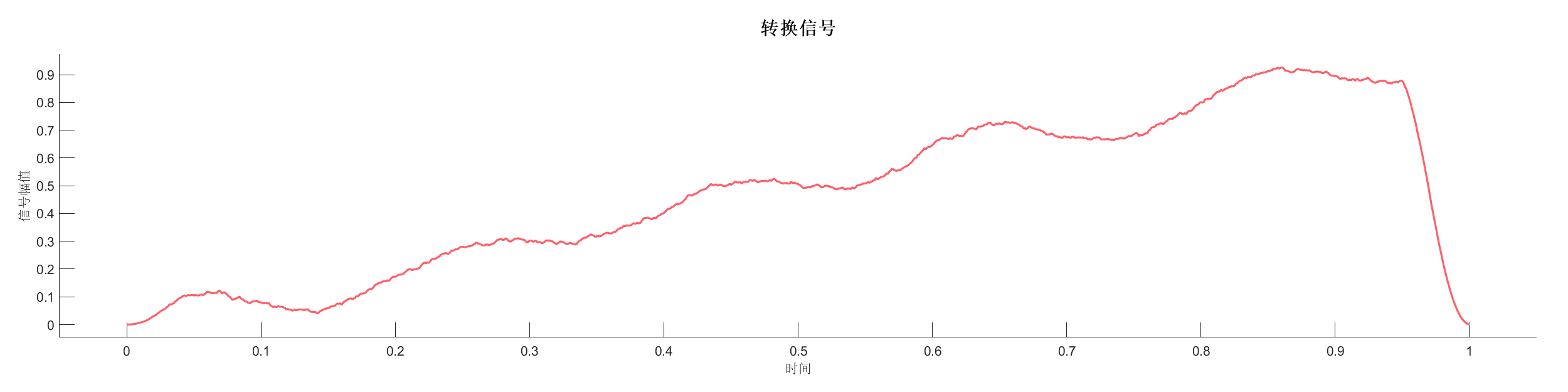
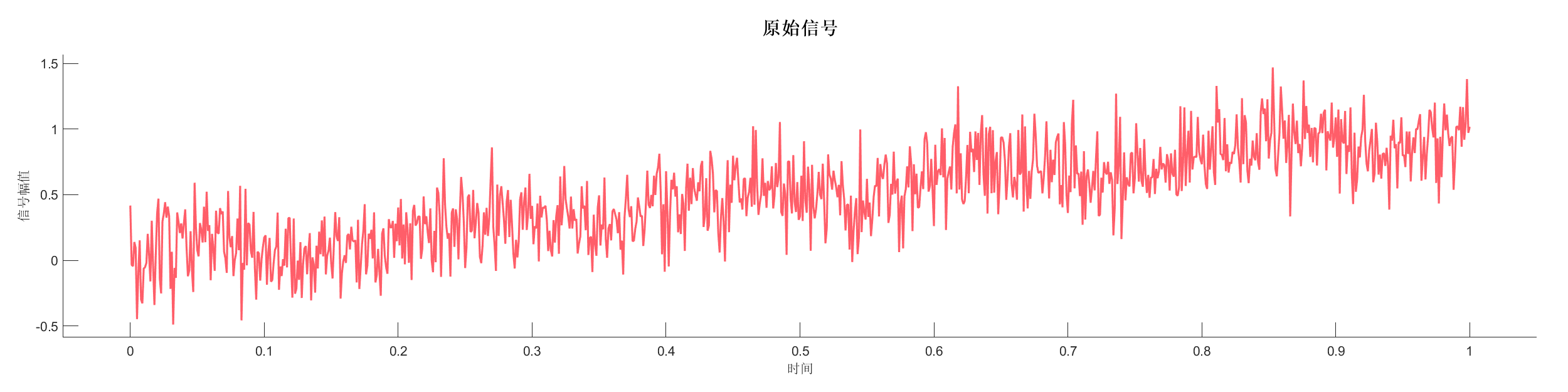
源代码：

% 基本参数设置
dt = .001;  % 时间采样间隔 [s]
tmax = 1;   % 信号总时长 [s]
t = 0:dt:tmax;  % 时间向量

% 创建测试信号
f1 = 5;  % 正弦波频率 [Hz]
a1 = .1; a2 = 1;  % 振幅系数
s = a1*sin(2*pi*f1*t) + a2*t;  % 合成信号：低频正弦波 + 线性趋势

% 添加随机噪声
n = .2*randn(size(t));  % 生成高斯白噪声（标准差为0.2）
sn = s + n;  % 含噪信号 = 原始信号 + 噪声

% 输入结构
inputStruct.t = t;
inputStruct.s = sn;

% 参数结构
paramsStruct.Name = 'Demo8_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = SignalSmooth(SA1, 'window','box','tsmo',0.1);
PlotTransformSignal(SA1);

SA1 = SignalSmooth(SA1, 'window','tri','tsmo',0.1);
PlotTransformSignal(SA1);

SA1 = SignalSmooth(SA1, 'window','gauss','tsmo',0.1);
PlotTransformSignal(SA1);

Demo9 - 高斯低通滤波

案例介绍：

生成合成地震记录，使用高斯低通滤波和频域滤波去除噪声，对比不同滤波方法的效果。

图表：

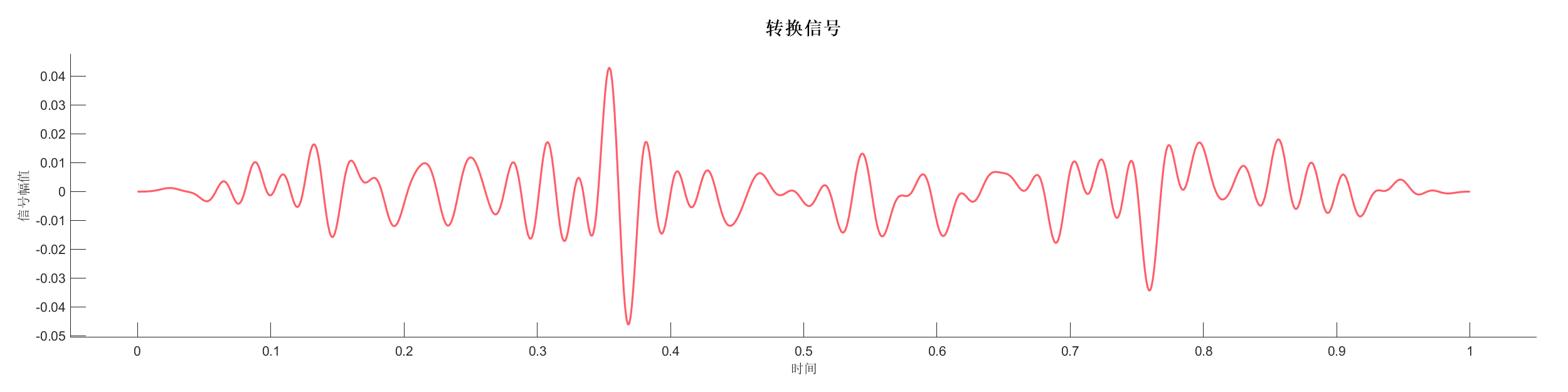
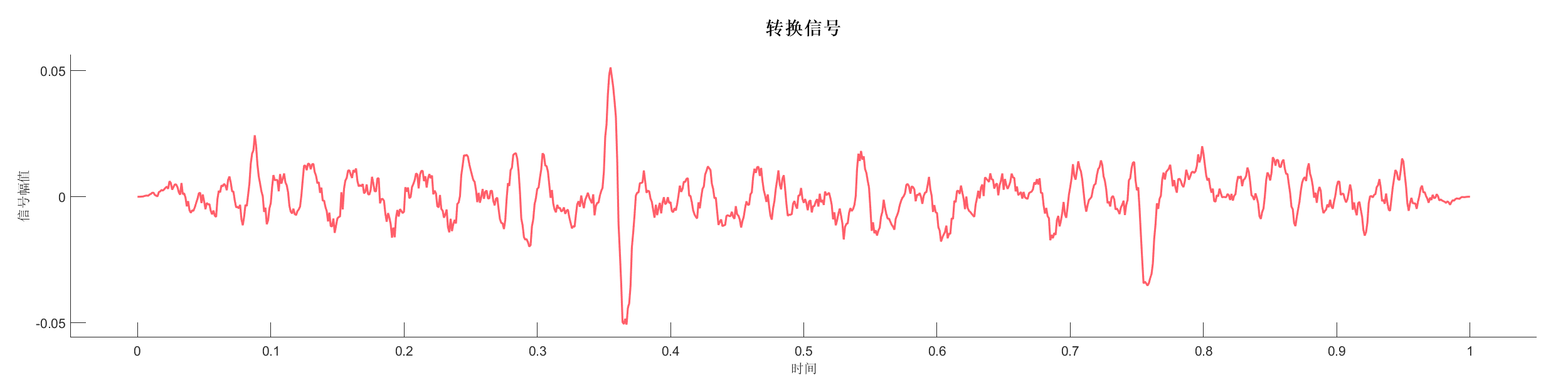
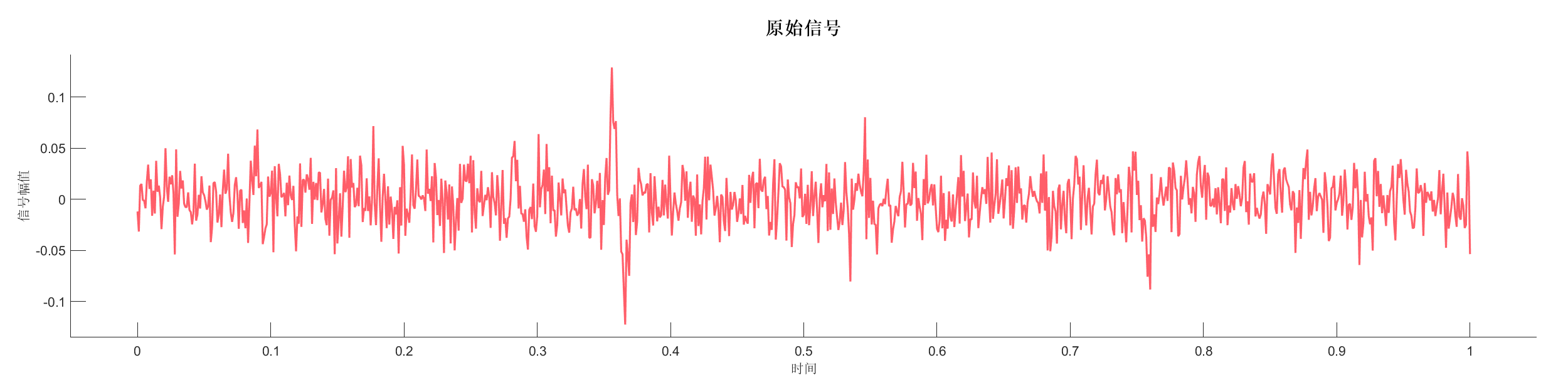
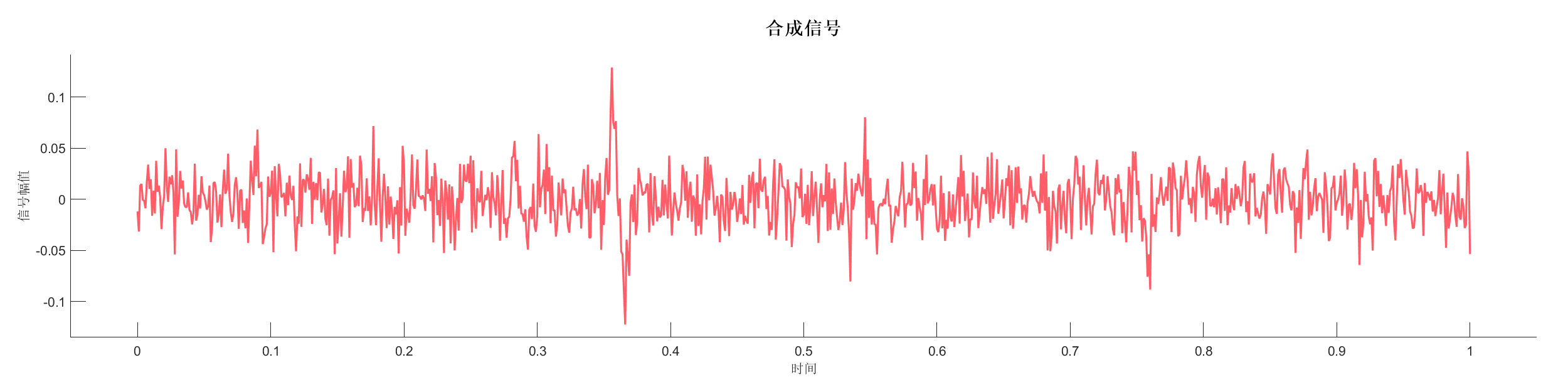
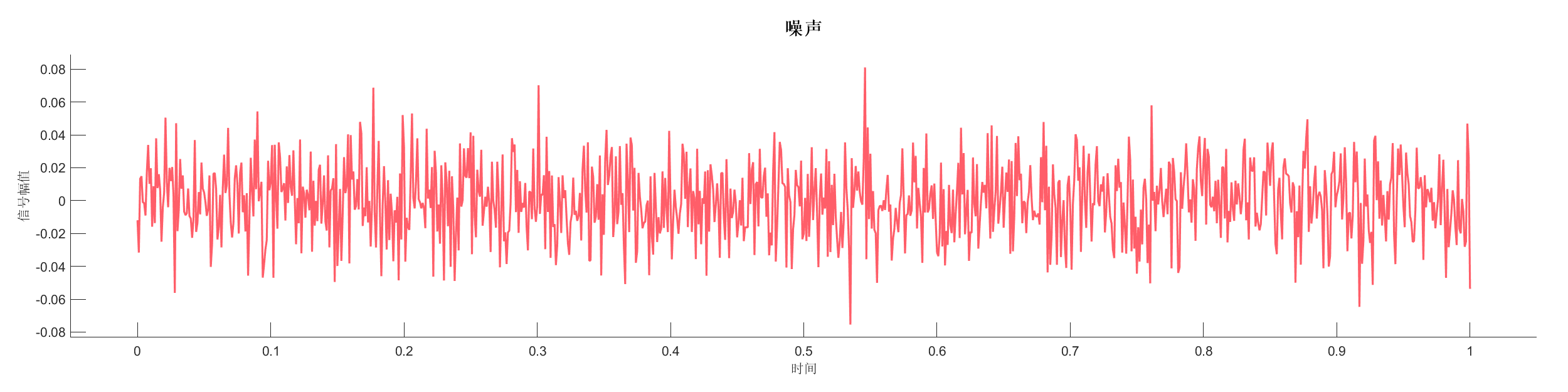
源代码：

% 基本参数设置
dt = .001;  % 时间采样间隔 [s]
tmax = 1.0;  % 反射系数序列长度 [s]
fdom = 30;  % 小波主频 [Hz]
tlen = .2;  % 小波长度 [s]
s2n = .5;  % 信噪比（信号与噪声的能量比）

% 创建合成地震记录
[r, t] = reflec(tmax, dt, .1, 5, 3);  % 生成反射系数序列 r 和时间坐标 t

% 输入结构
inputStruct.t = t;
inputStruct.s = r;

% 参数结构
paramsStruct.Name = 'Temp';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();
PlotOriSignal(SA);

SA = WaveletTransform(SA, 'WaveType','min','tlength',tlen,'fdom',fdom);

% 添加随机噪声
n1 = rnoise(SA.output.s_Transform, s2n);  % 生成与 s1 信噪比为 s2n 的噪声
SA = AddNoise(SA, n1);
PlotNoise(SA);
PlotSyntheticSignal(SA);

% 输入结构
inputStruct.t = t;
inputStruct.s = SA.output.s_Synthesis;

% 参数结构
paramsStruct.Name = 'Demo9_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = SignalSmooth(SA1, 'window','box','tsmo',0.01);
PlotTransformSignal(SA1);

% 使用频域低通滤波进行对比
SA1 = SignalSmooth(SA1, 'method','bandpass','fmin',0,'fmax',[45 5]);
PlotTransformSignal(SA1);

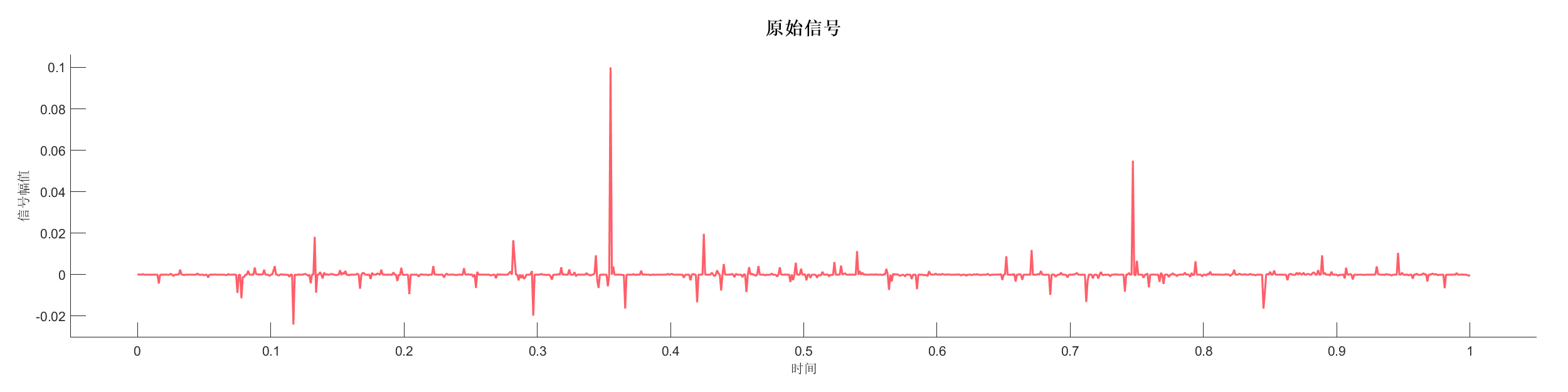
Demo10 - 快速傅里叶变换 (FFT)

案例介绍：

加载实测信号数据，进行快速傅里叶变换分析，展示信号的频域特性。

图表：

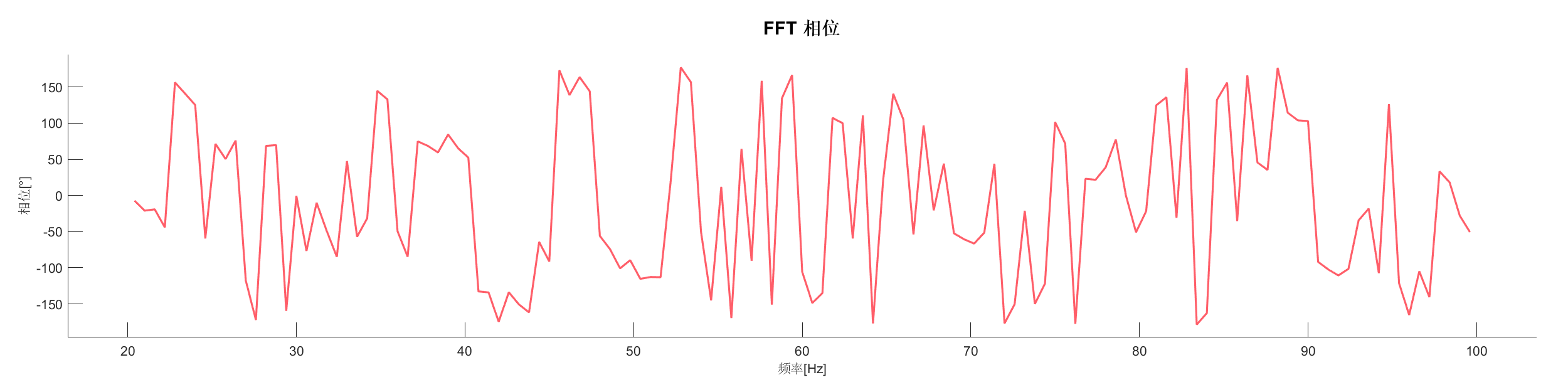
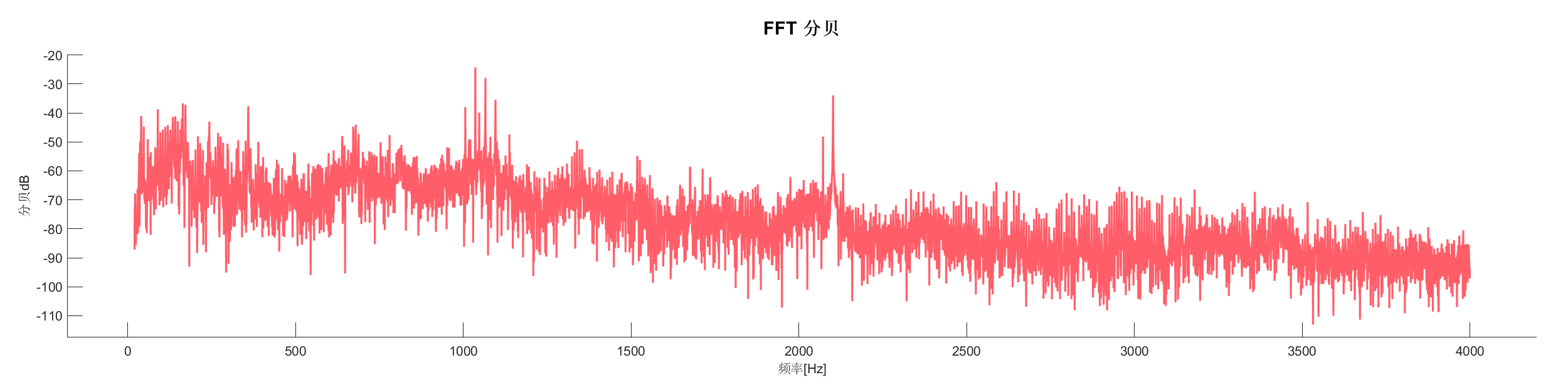
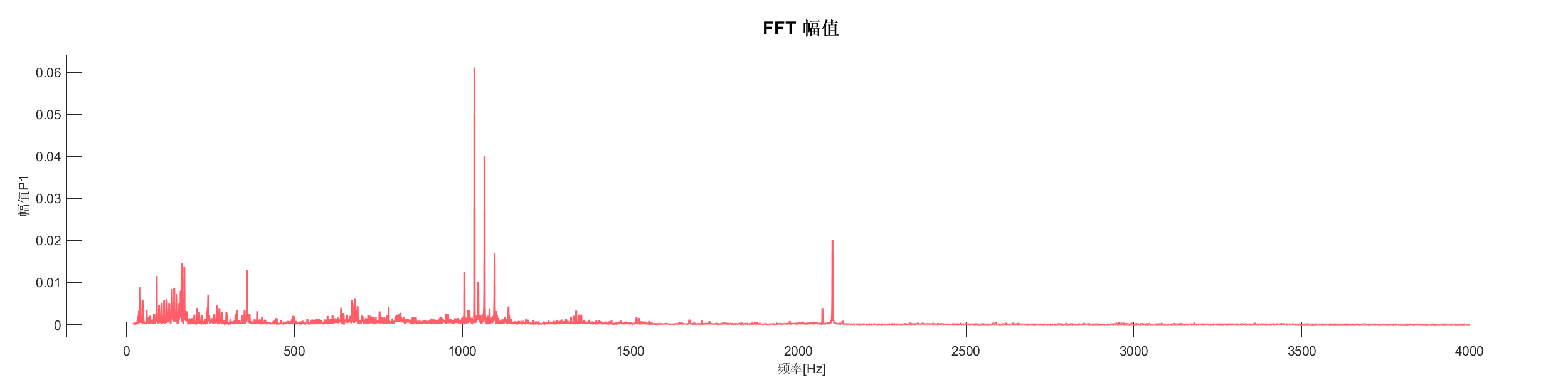
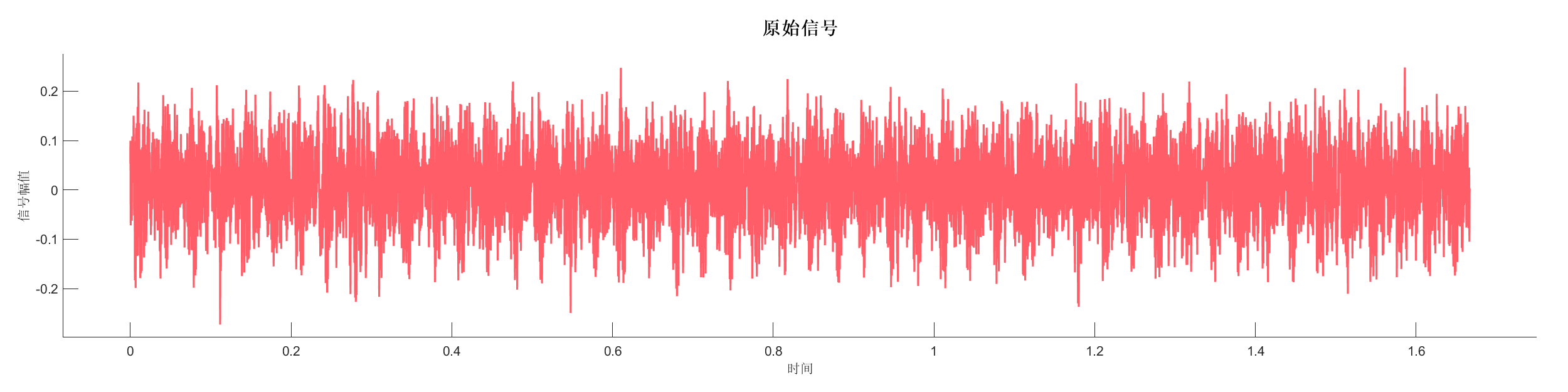
源代码：

data = load('97.mat');
Start = 1;
DataNum = 20000;
x = data.X097_DE_time(Start:Start+DataNum,:)';
Fs = 12000;
dt = 1/Fs;  % 时间采样间隔 [s]
t = (0:DataNum)*dt;  % time coordinate vector

% 输入结构
inputStruct.t = t;
inputStruct.s = x;

% 参数结构
paramsStruct.Name = 'Demo10_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = FFT(SA1);
PlotFFT(SA1,'Freq',[20,4000]);
PlotdB(SA1,'Freq',[20,4000]);
PlotPhase(SA1,'Freq',[20,100]);

Demo11 - 同步挤压变换 (SST)

案例介绍：

使用同步挤压变换 (SST) 对实测信号进行时频分析，提高时频分辨率。

图表：

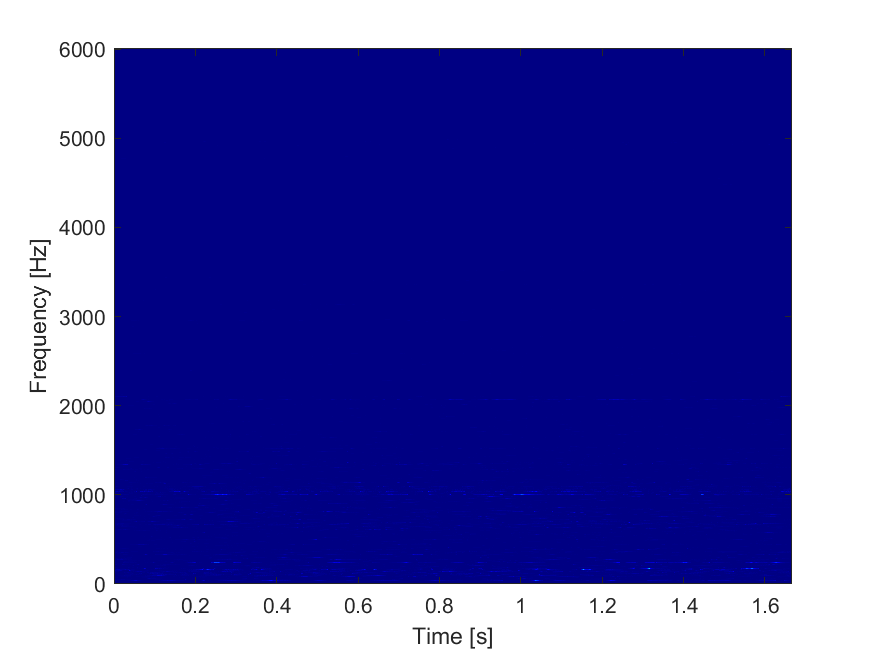
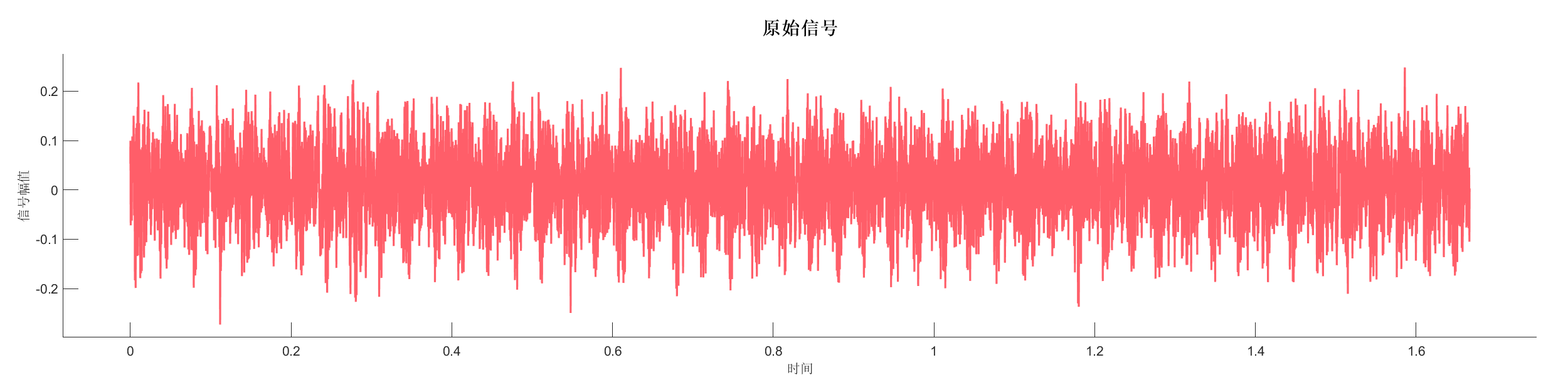
源代码：

data = load('97.mat');
Start = 1;
DataNum = 20000;
x = data.X097_DE_time(Start:Start+DataNum,:)';
Fs = 12000;
dt = 1/Fs;  % 时间采样间隔 [s]
t = (0:DataNum)*dt;  % time coordinate vector

% 输入结构
inputStruct.t = t;
inputStruct.s = x;

% 参数结构
paramsStruct.Name = 'Demo11_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = SST(SA1,'hlength',2000);
PlotSST(SA1);

Demo12 - 瞬态提取变换 (TET)

案例介绍：

使用瞬态提取变换 (TET) 对实测信号进行瞬态特征提取，展示非平稳信号的时频特性。

图表：

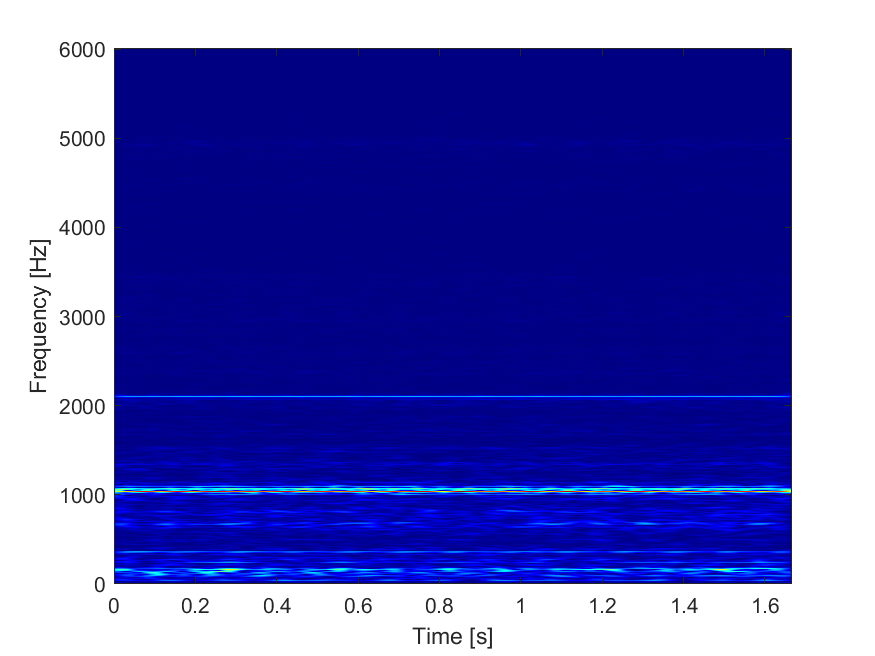
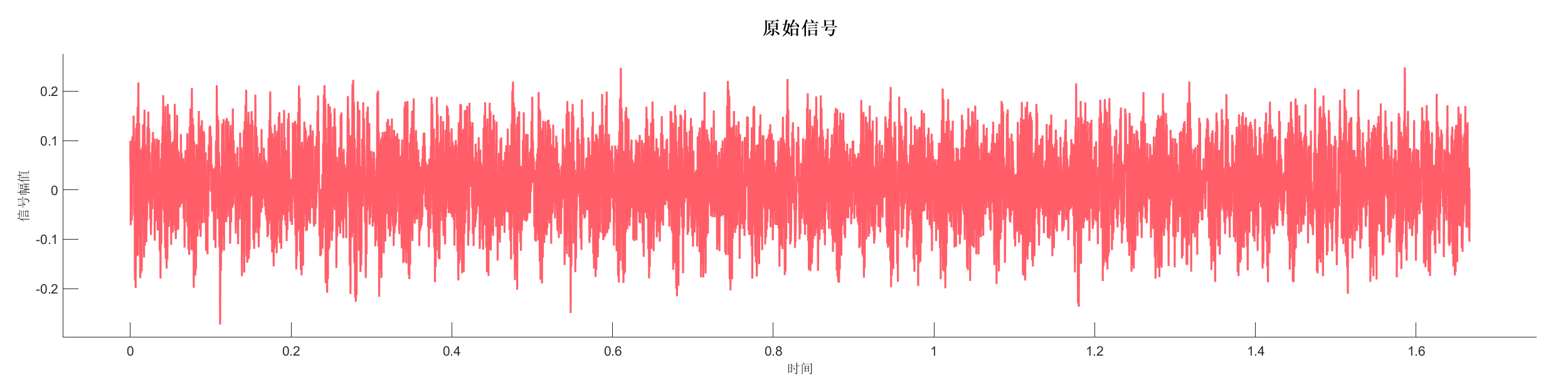
源代码：

data = load('97.mat');
Start = 1;
DataNum = 20000;
x = data.X097_DE_time(Start:Start+DataNum,:)';
Fs = 12000;
dt = 1/Fs;  % 时间采样间隔 [s]
t = (0:DataNum)*dt;  % time coordinate vector

% 输入结构
inputStruct.t = t;
inputStruct.s = x;

% 参数结构
paramsStruct.Name = 'Demo11_1';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = TET(SA1,'hlength',2000);
PlotTET(SA1);

Demo13 - 小波变换 (WT)

案例介绍：

使用连续小波变换 (WT) 对实测信号进行多尺度时频分析。

图表：

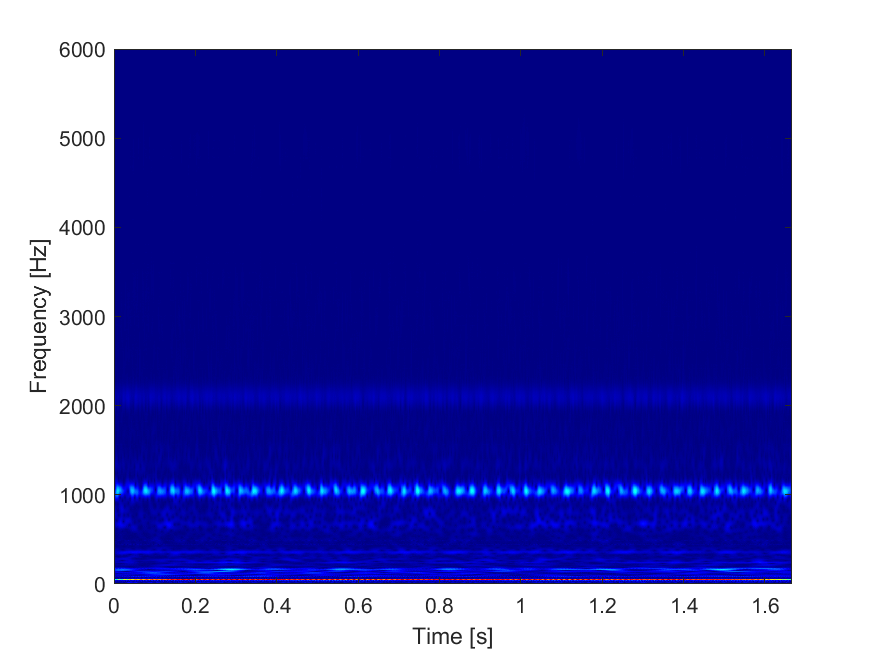
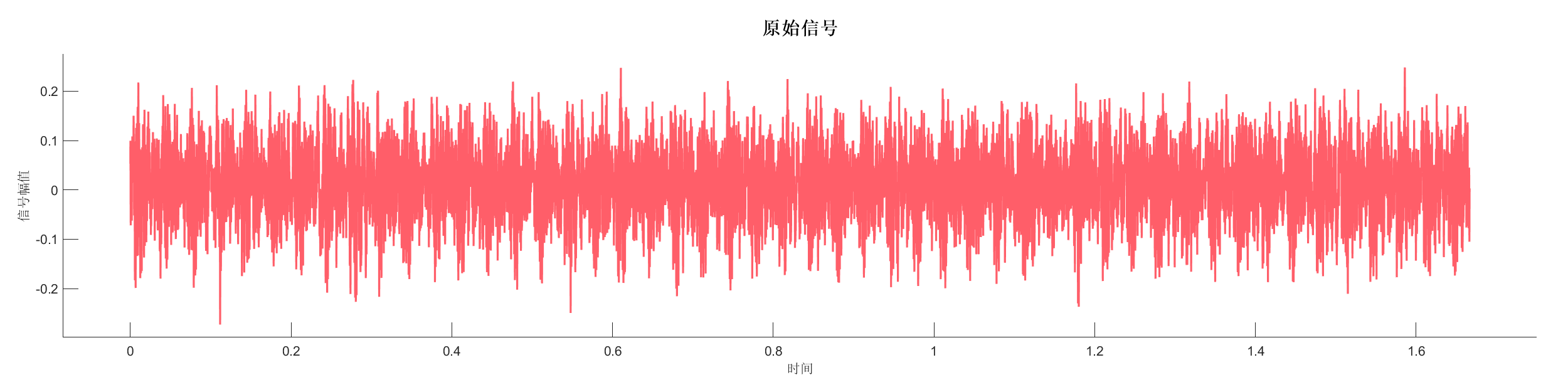
源代码：

data = load('97.mat');
Start = 1;
DataNum = 20000;
x = data.X097_DE_time(Start:Start+DataNum,:)';
Fs = 12000;
dt = 1/Fs;  % 时间采样间隔 [s]
t = (0:DataNum)*dt;  % time coordinate vector

% 输入结构
inputStruct.t = t;
inputStruct.s = x;

% 参数结构
paramsStruct.Name = 'Demo13';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = WT(SA1,'hlength',2000);
PlotWT(SA1);

Demo14 - 希尔伯特变换

案例介绍：

使用希尔伯特变换对正弦波信号进行解析信号分析，计算瞬时相位和幅值。

图表：

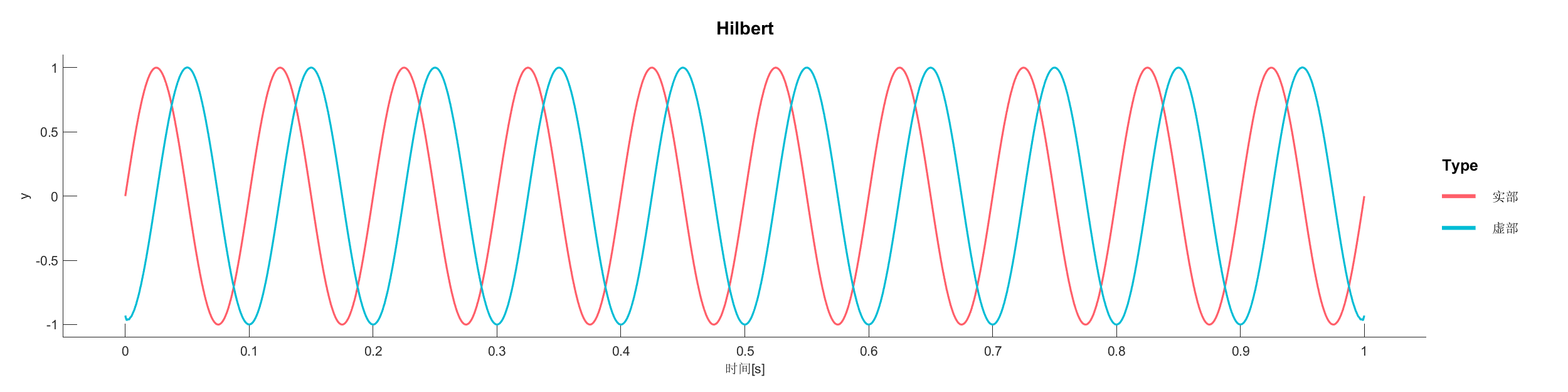
源代码：

t = 0:.001:1;  % make a time axis
f = 10;  % we will make a 10 Hz signal
s = sin(2*pi*f*t);  % 10 Hz sine wave

% 输入结构
inputStruct.t = t;
inputStruct.s = s;

% 参数结构
paramsStruct.Name = 'Demo14';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = Hilbert(SA1);
PlotHilbert(SA1);

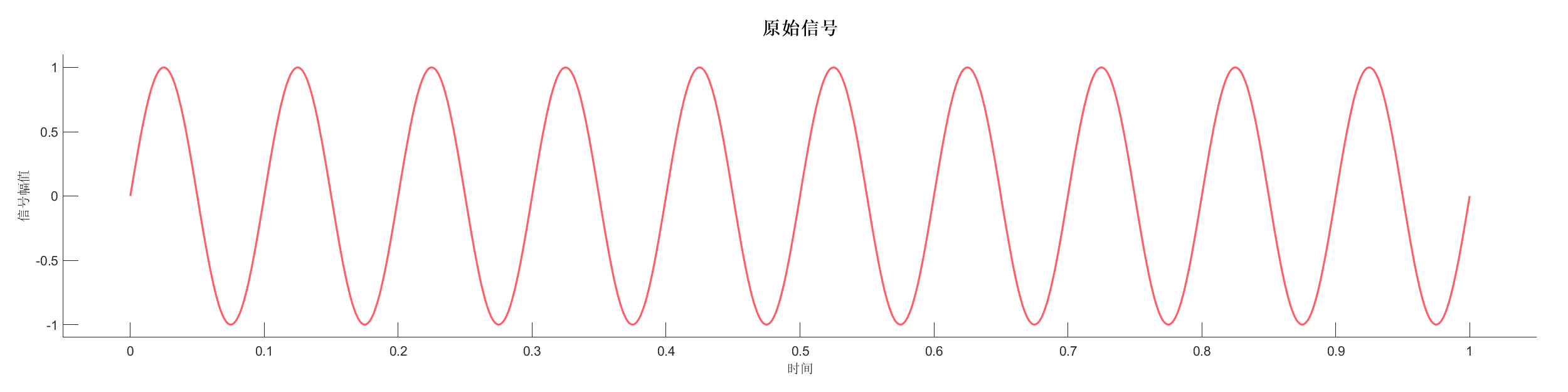
Demo15 - 信号包络

案例介绍：

使用希尔伯特变换提取信号包络，分析信号的包络特性。

图表：

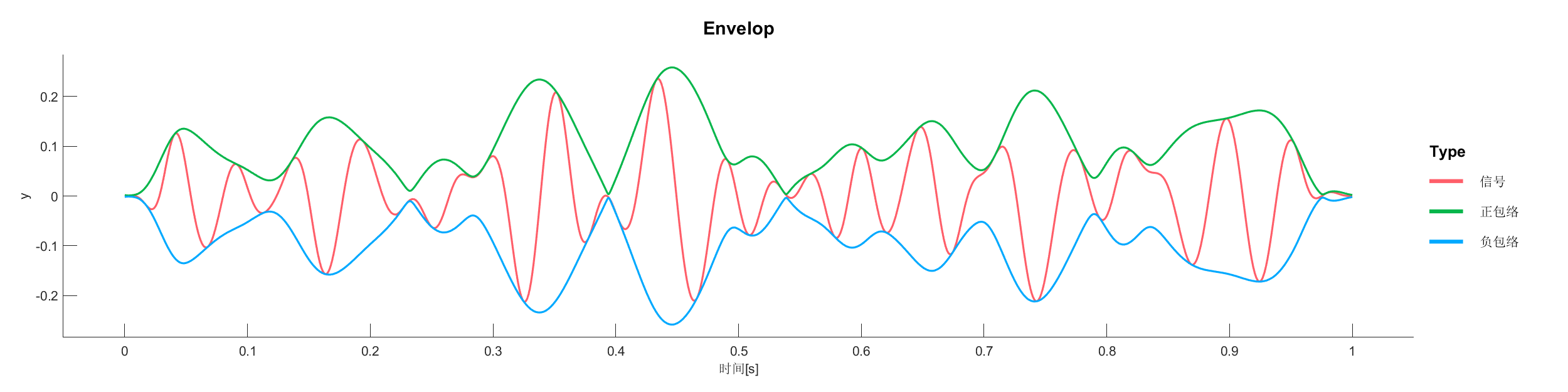
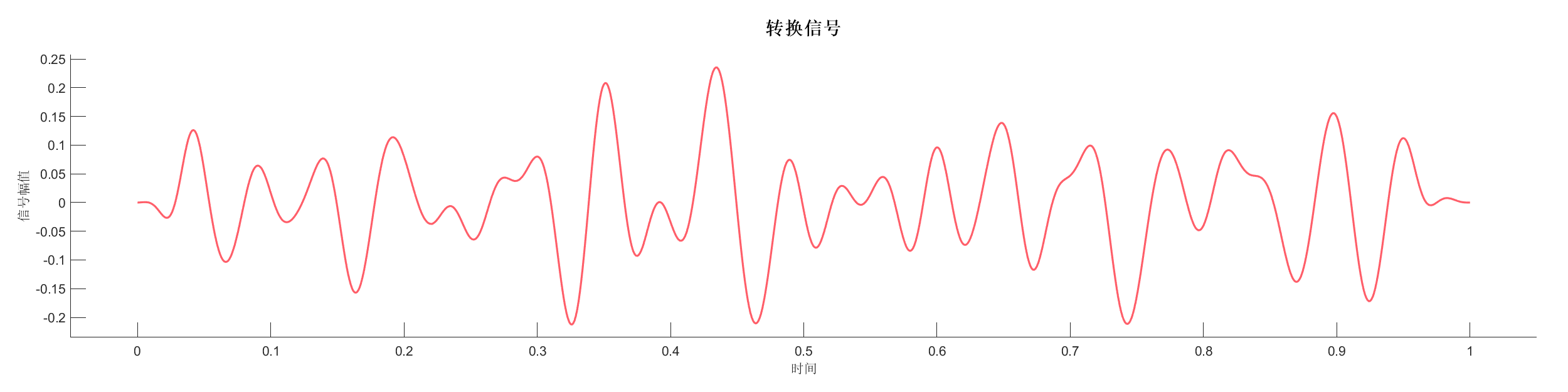
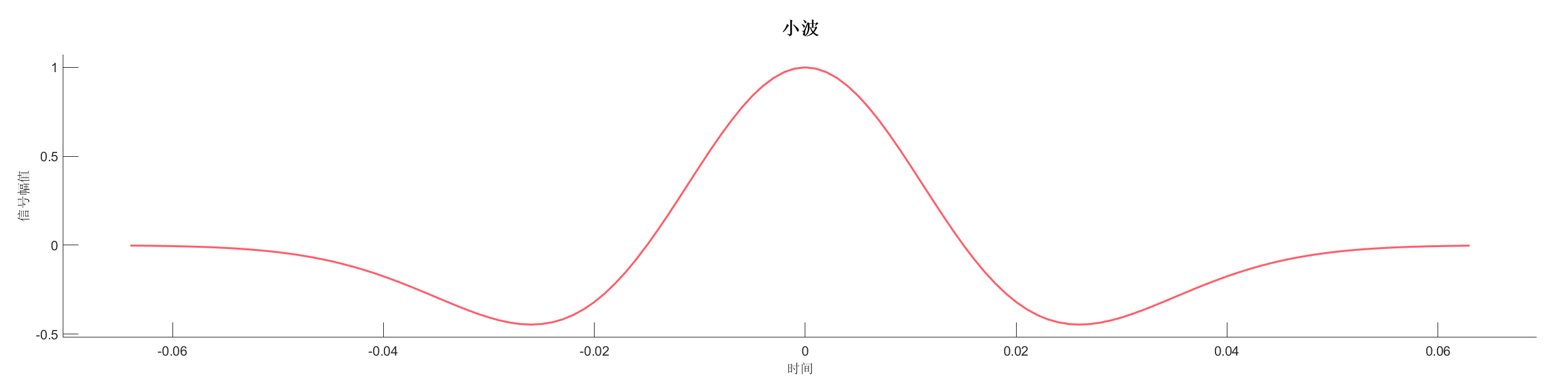
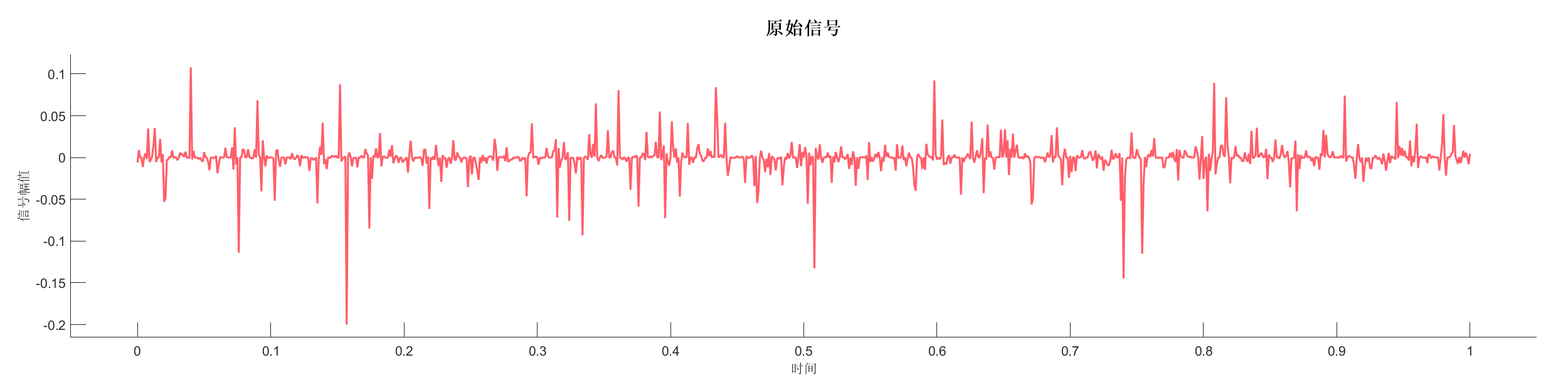
源代码：

[r, t] = reflec(1, .001);  % make a reflectivity

% 输入结构
inputStruct.t = t;
inputStruct.s = r;

% 参数结构
paramsStruct.Name = 'Demo15';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = WaveletTransform(SA1);
PlotWavelet(SA1);
PlotTransformSignal(SA1);

SA1 = Envelop(SA1,'Type',1);
PlotEnvelop(SA1,'Type',1);

Demo16 - 识别主频率

案例介绍：

使用不同的主频识别方法分析信号的主频成分，展示不同方法的差异。

图表：

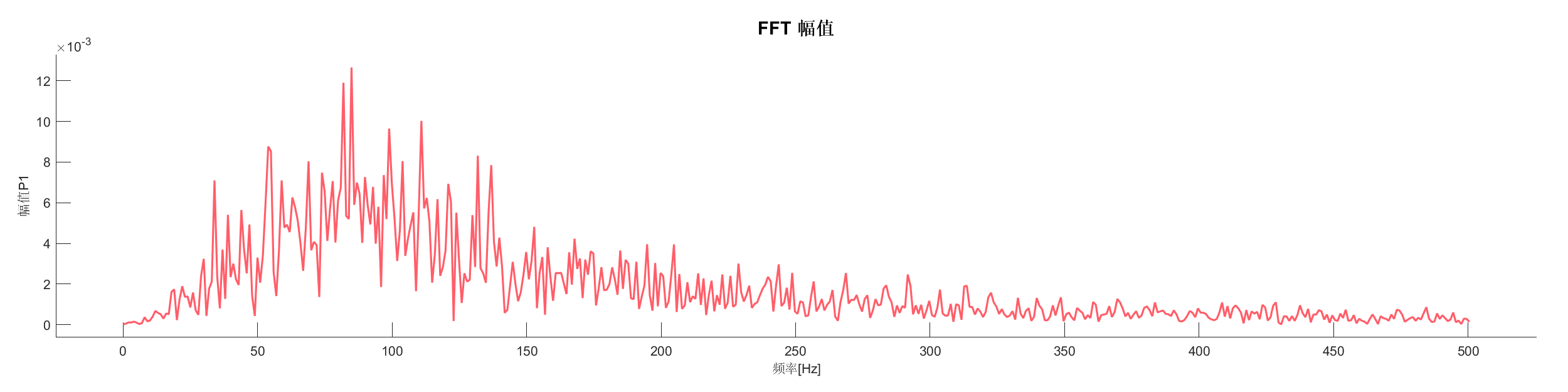
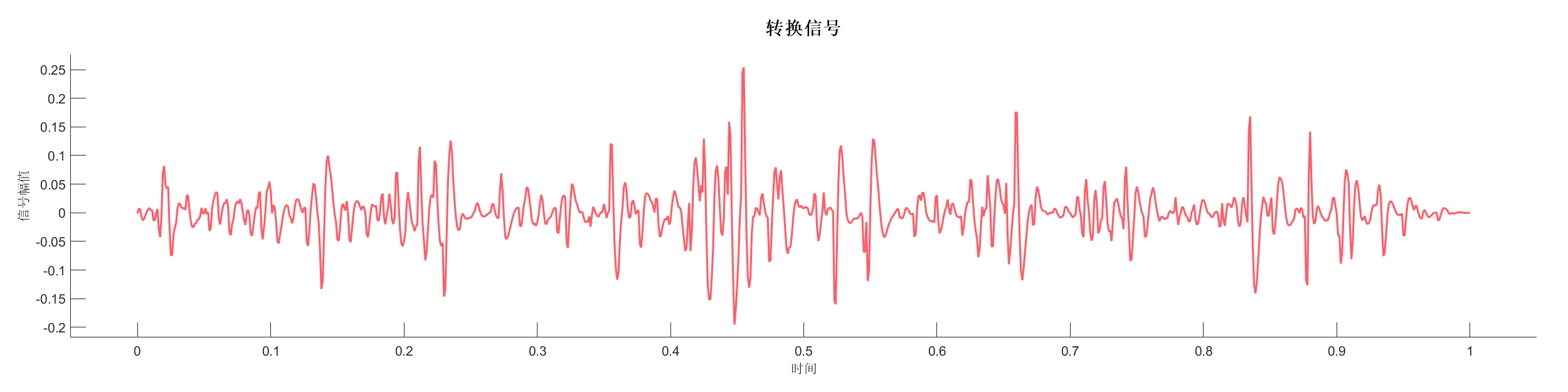
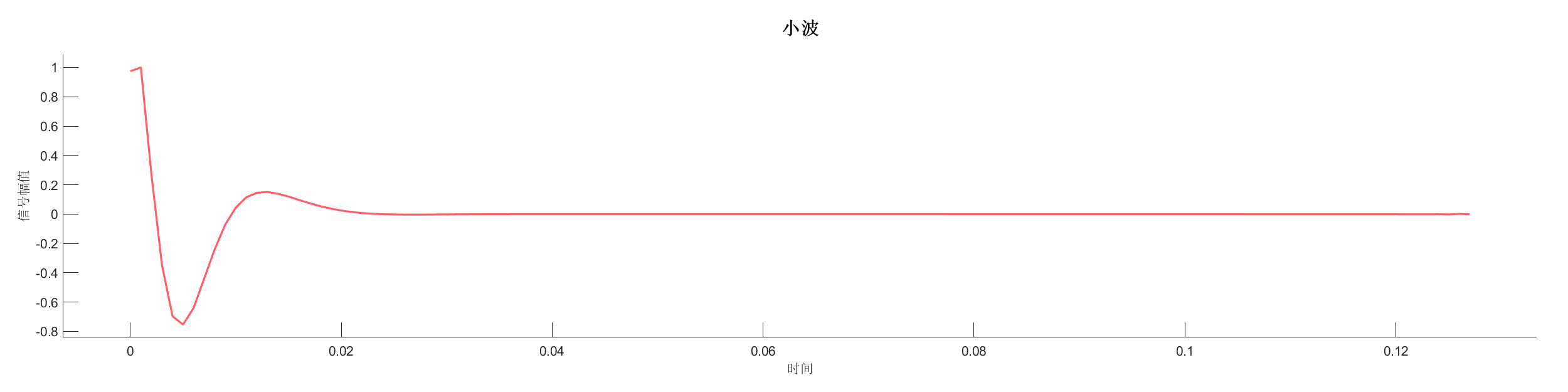
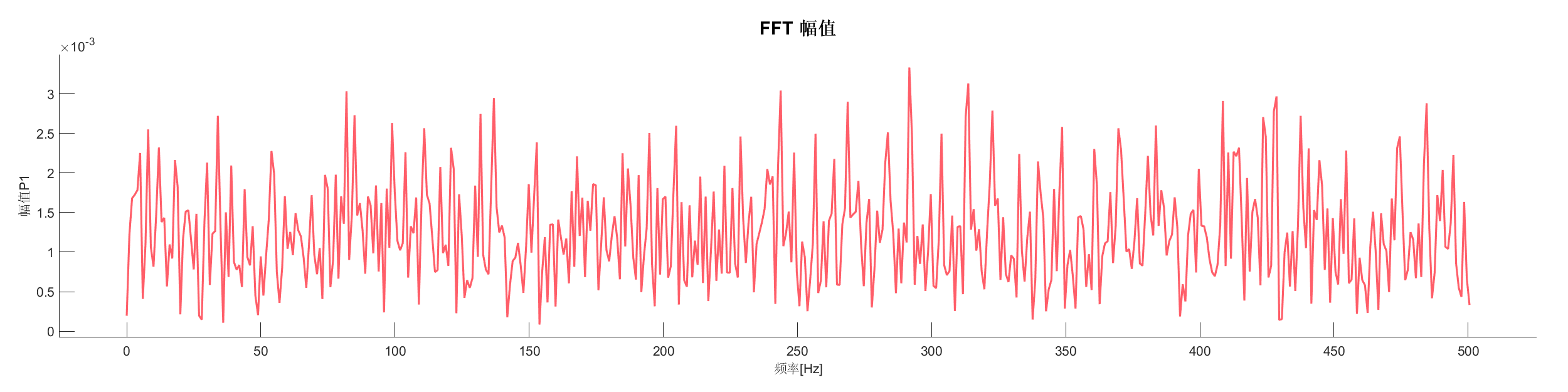
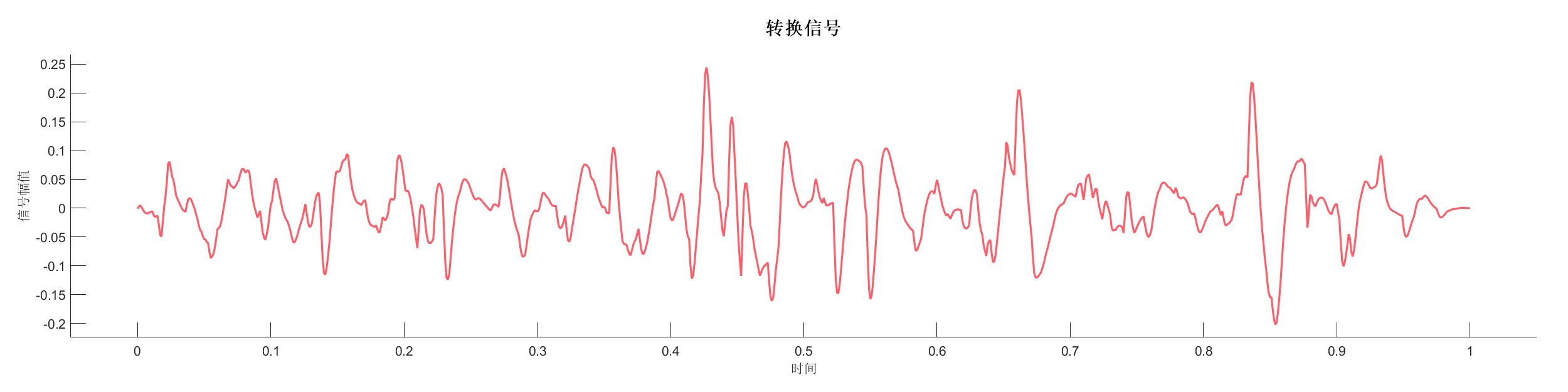
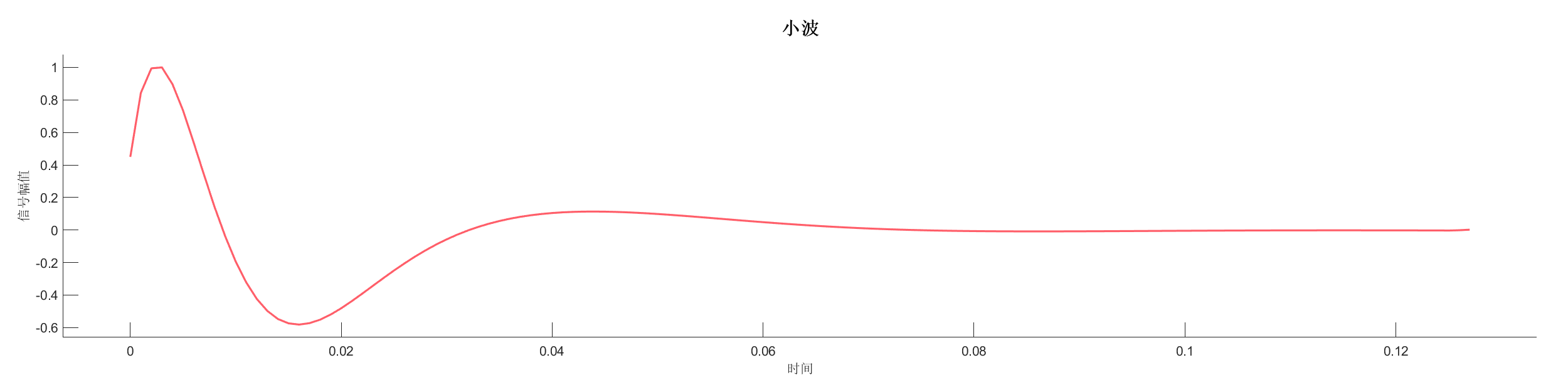
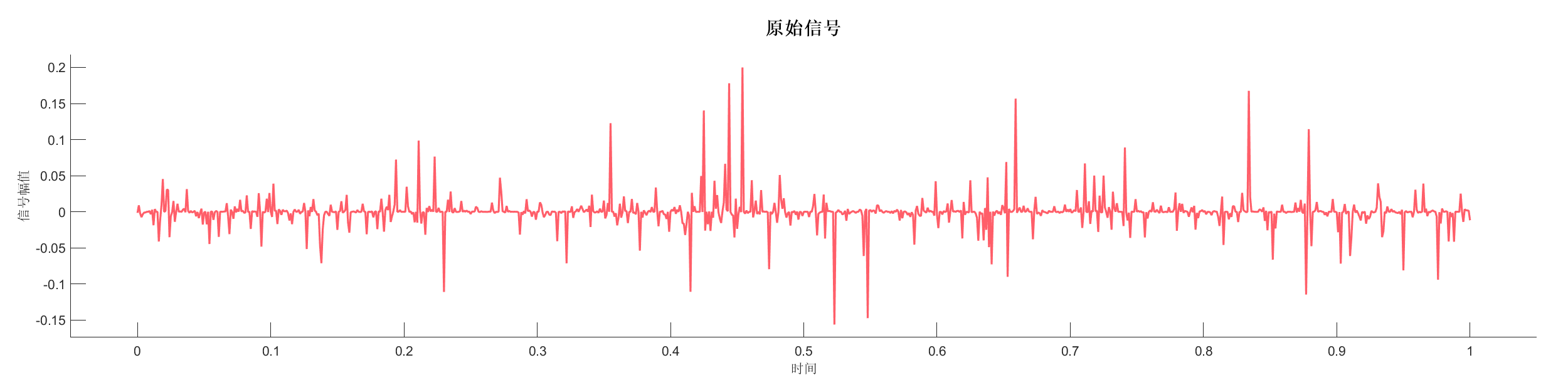
源代码：

% 参数设置
f1 = 20;  % 第一个子波的中心频率 (Hz)
f2 = 60;  % 第二个子波的中心频率 (Hz)

[r, t] = reflec(1, .001);  % make a reflectivity

% 输入结构
inputStruct.t = t';
inputStruct.s = r';

% 参数结构
paramsStruct.Name = 'Demo16';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();
PlotOriSignal(SA1);

SA1 = WaveletTransform(SA1,'WaveType','min','fdom',f1);
PlotWavelet(SA1);
PlotTransformSignal(SA1);

SA1 = FreqDom(SA1,'Type',1,'p',2);
SA1 = FFT(SA1,'Type',0);
PlotFFT(SA1,'Type',0);

SA1 = WaveletTransform(SA1,'WaveType','min','fdom',f2);
PlotWavelet(SA1);
PlotTransformSignal(SA1);

SA1 = FreqDom(SA1,'Type',1,'p',2);
SA1 = FreqDom(SA1,'Type',1,'p',2);
SA1 = FFT(SA1,'Type',1);
PlotFFT(SA1,'Type',1);

Demo17 - 巴特沃斯滤波

案例介绍：

使用巴特沃斯带通滤波器对信号进行滤波，去除高频噪声。

图表：

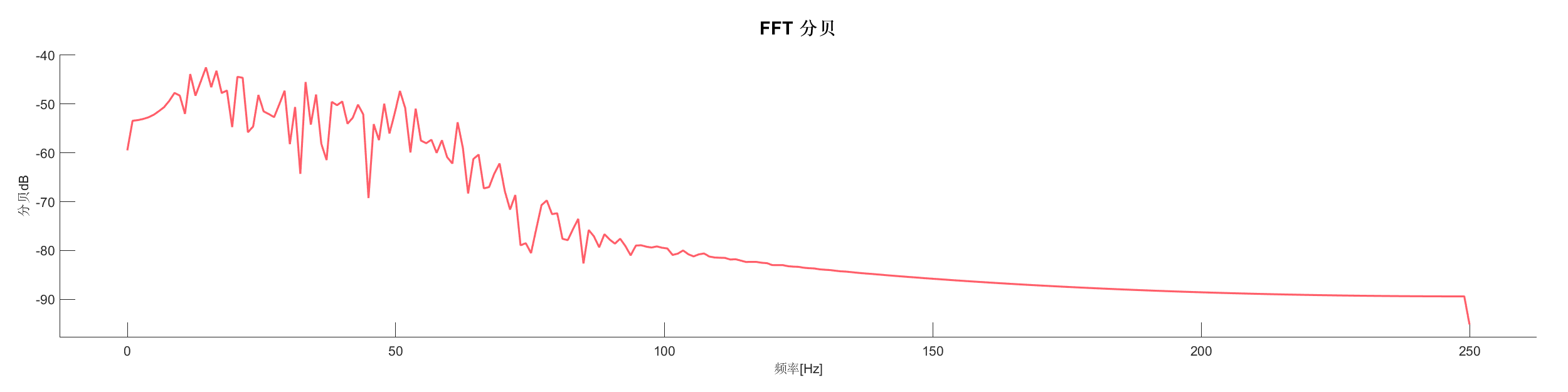
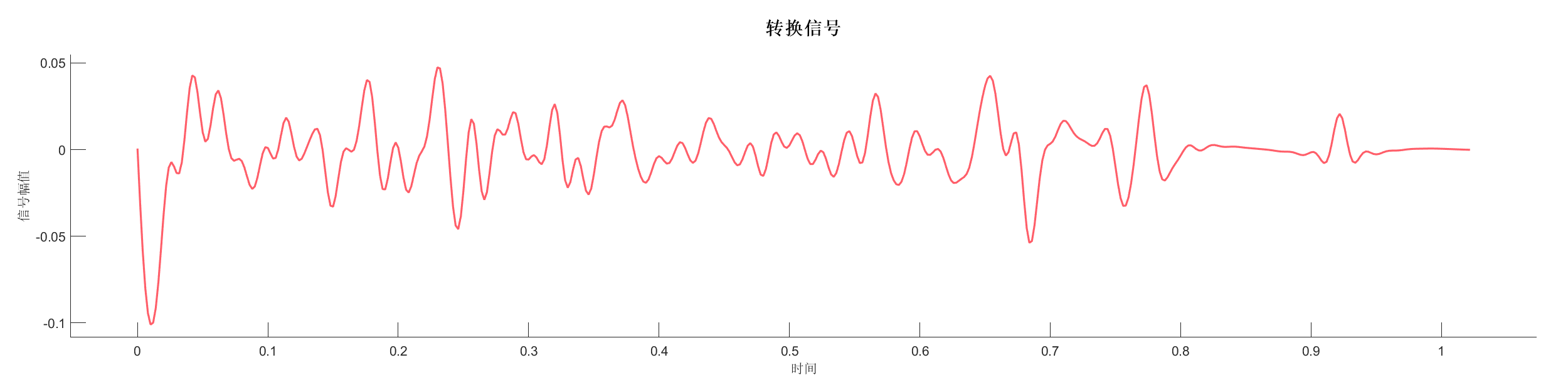
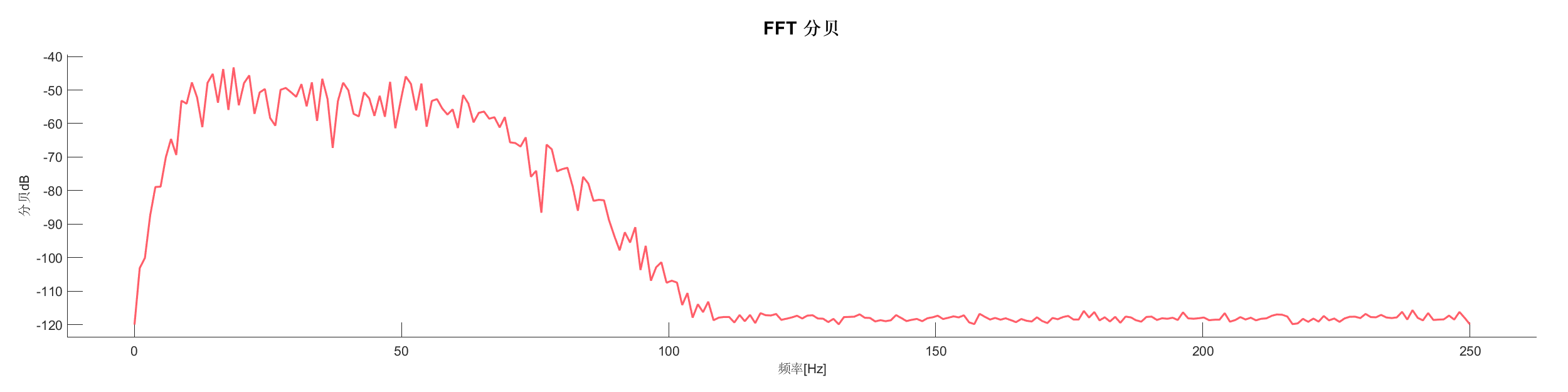
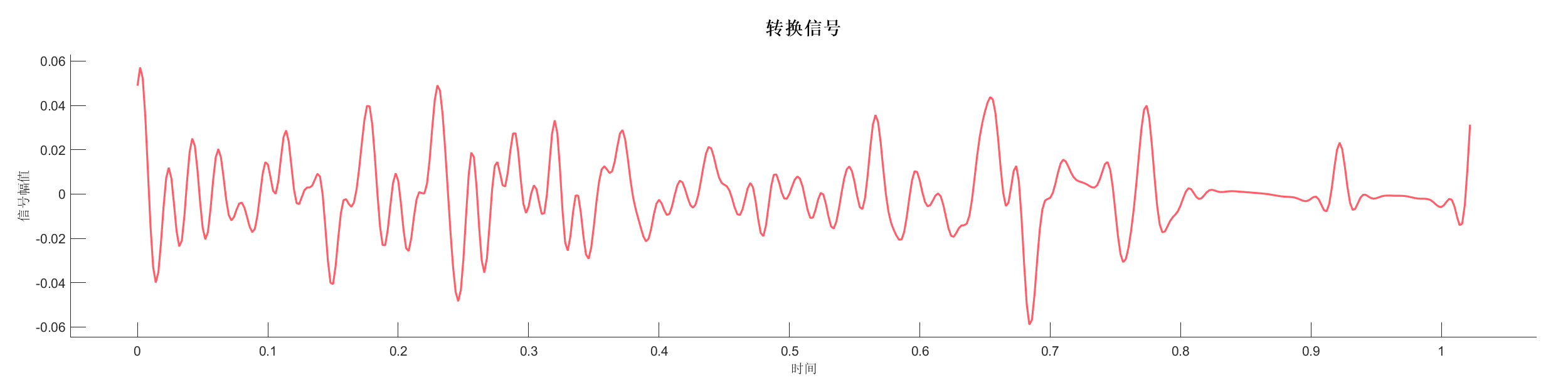
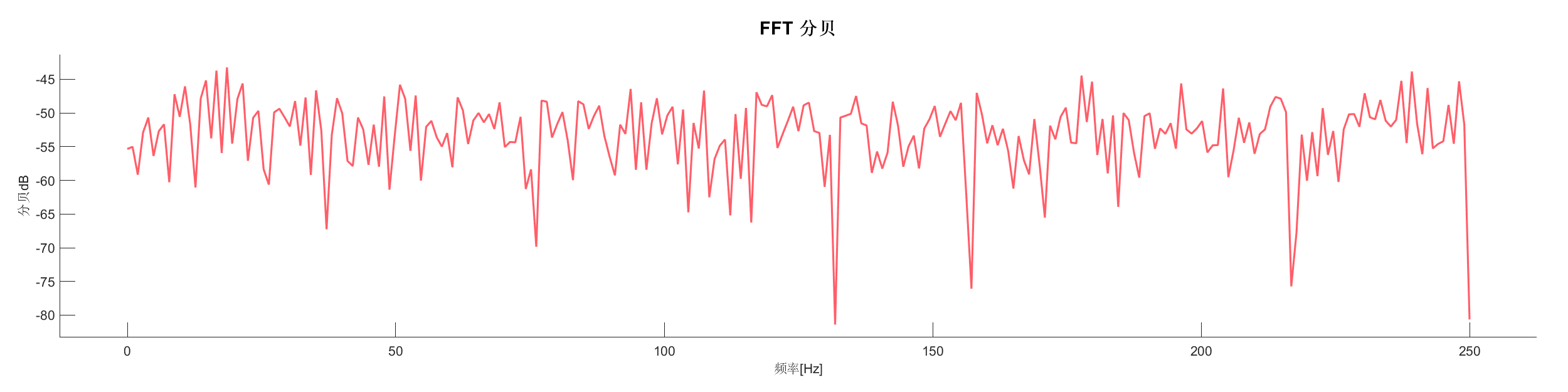
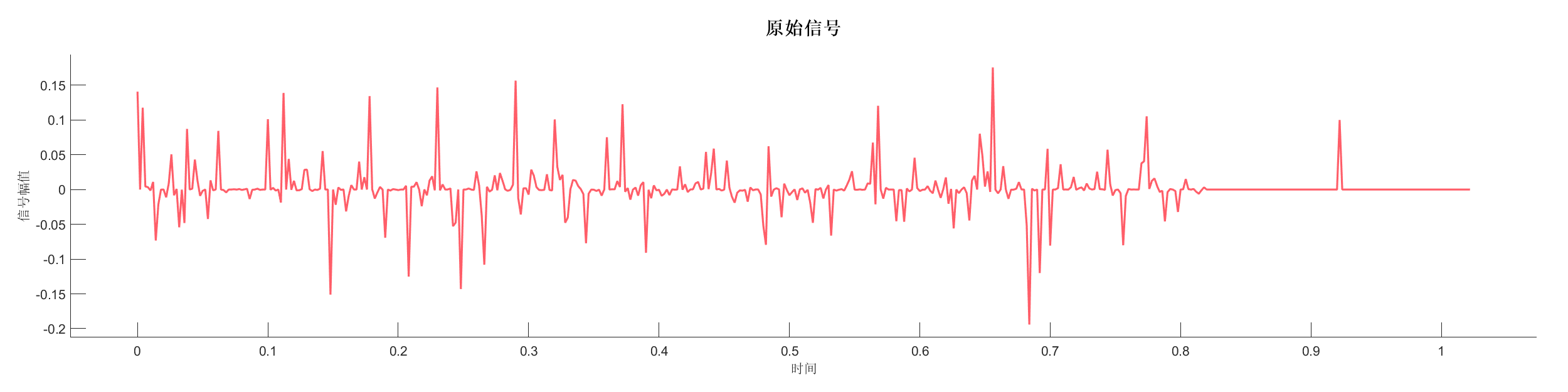
源代码：

dt = .002;  % 时间采样间隔
tmax = 1.022;  % 选择此值使长度为2的幂次
[r, t] = reflec(tmax, dt, .2, 3, 4);  % 生成反射系数序列
r(end-100:end) = 0;  % 将最后100个采样点置零
r(end-50) = .1;  % 在零值区域中间放置一个尖峰
fmin = [10 5]; fmax = [60 20];  % 用于 filtf 函数的频率参数
n = 4;  % 巴特沃斯滤波器阶数

% 输入结构
inputStruct.t = t';
inputStruct.s = r';

% 参数结构
paramsStruct.Name = 'Demo17';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();
PlotOriSignal(SA);

SA = FFT(SA);
PlotdB(SA);

SA = SignalSmooth(SA,'method','bandpass','fmin',fmin,'fmax',fmax);
PlotTransformSignal(SA);
SA = FFT(SA,'Type',1);
PlotdB(SA,'Type',1);

SA = SignalSmooth(SA,'method','butterband','fmin',fmin(1),'fmax',fmax(1),'n',n);
PlotTransformSignal(SA);
SA = FFT(SA,'Type',1);
PlotdB(SA,'Type',1);

Demo18 - Gabor 变换

案例介绍：

使用 Gabor 变换对线性调频信号（Chirp 信号）进行时频分析，展示 Gabor 变换的时频定位能力。

图表：

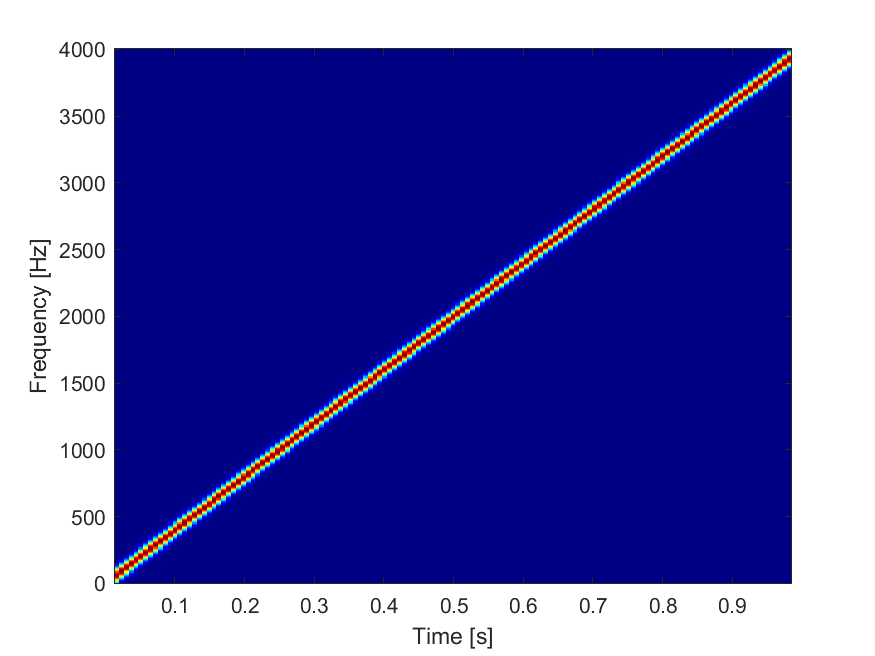
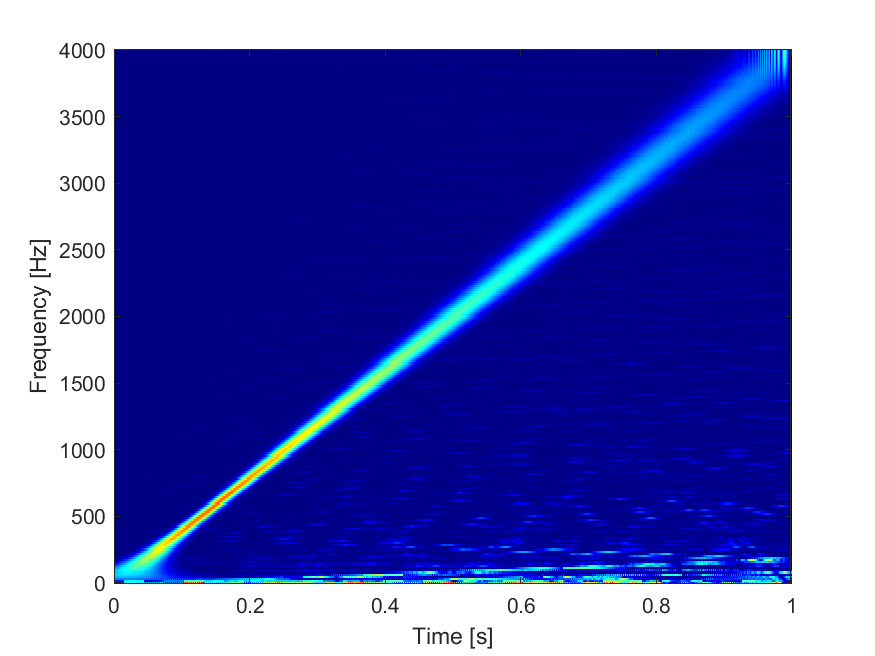
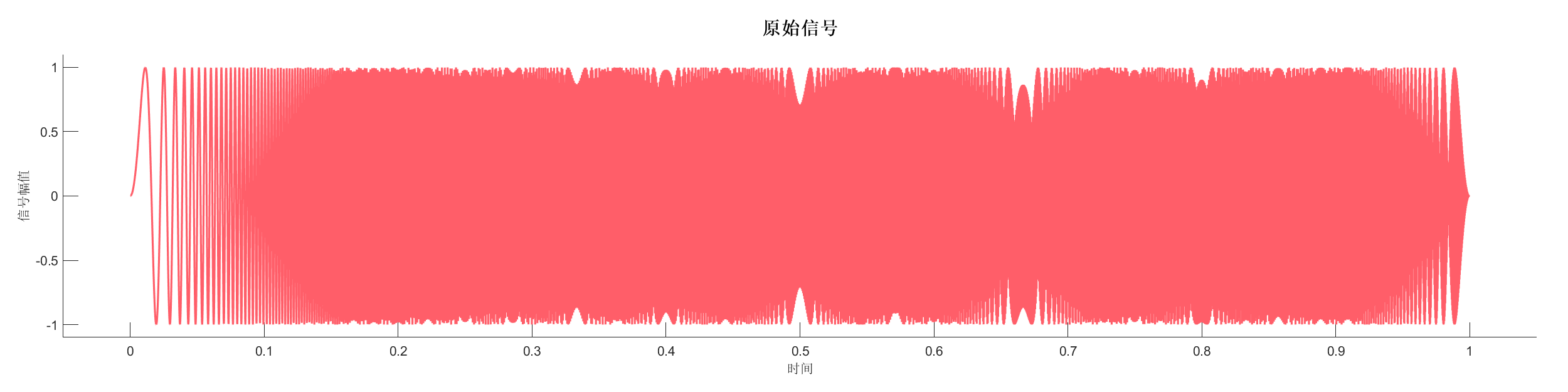
源代码：

% ========== Gabor Chirp（线性调频信号）==========
% 1秒线性调频信号，采样率为8000 Hz
Fs = 8000;  % 采样率
t = linspace(0,1,Fs);  % 时间向量（0到1秒）
x = sin(2*pi*2000*t.^2);  % 线性调频信号（从2000 Hz开始的线性调频）

% 输入结构
inputStruct.t = t;
inputStruct.s = x;

% 参数结构
paramsStruct.Name = 'Demo18';
paramsStruct.Echo = 1;

% 创建并求解 SignalAnalysis 对象
SA = signal.SignalAnalysis(paramsStruct, inputStruct);
SA = SA.solve();
PlotOriSignal(SA);

SA = WT(SA);
PlotWT(SA);

SA = Gabor(SA);
PlotGabor(SA);

Demo19 - 相关性分析

案例介绍：

演示三种相关性分析场景：

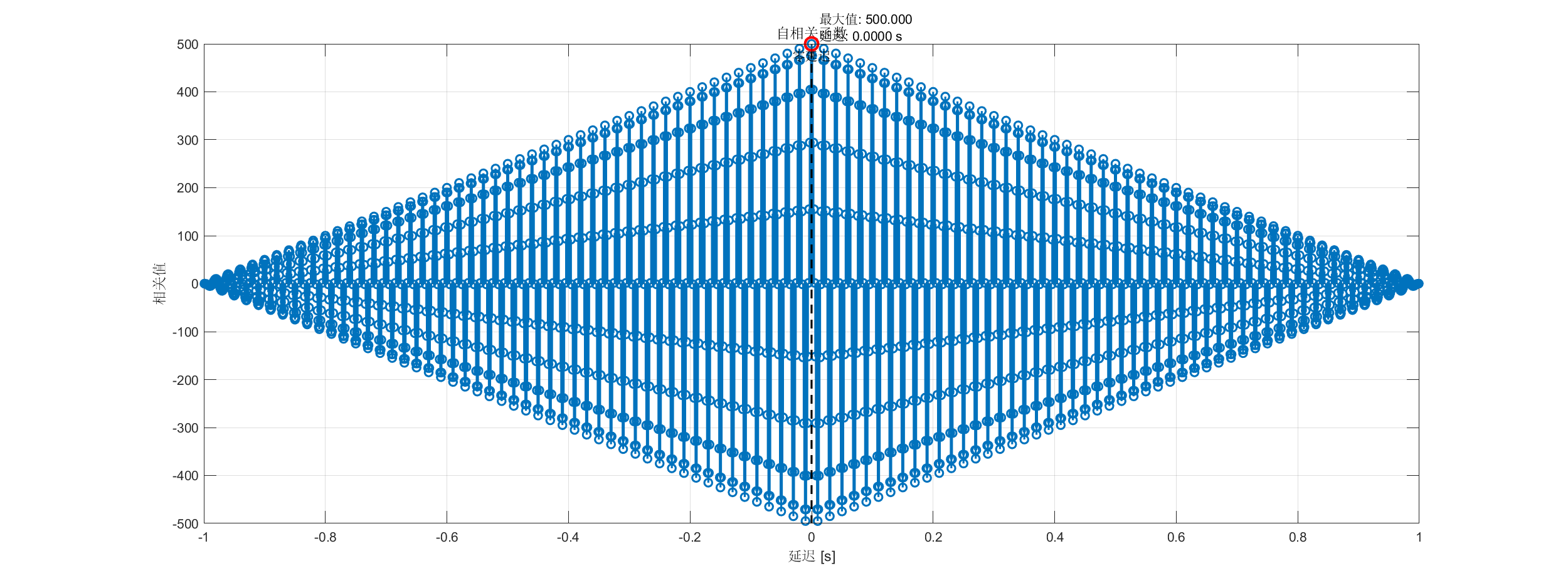
自相关分析 - 正弦波的自相关函数
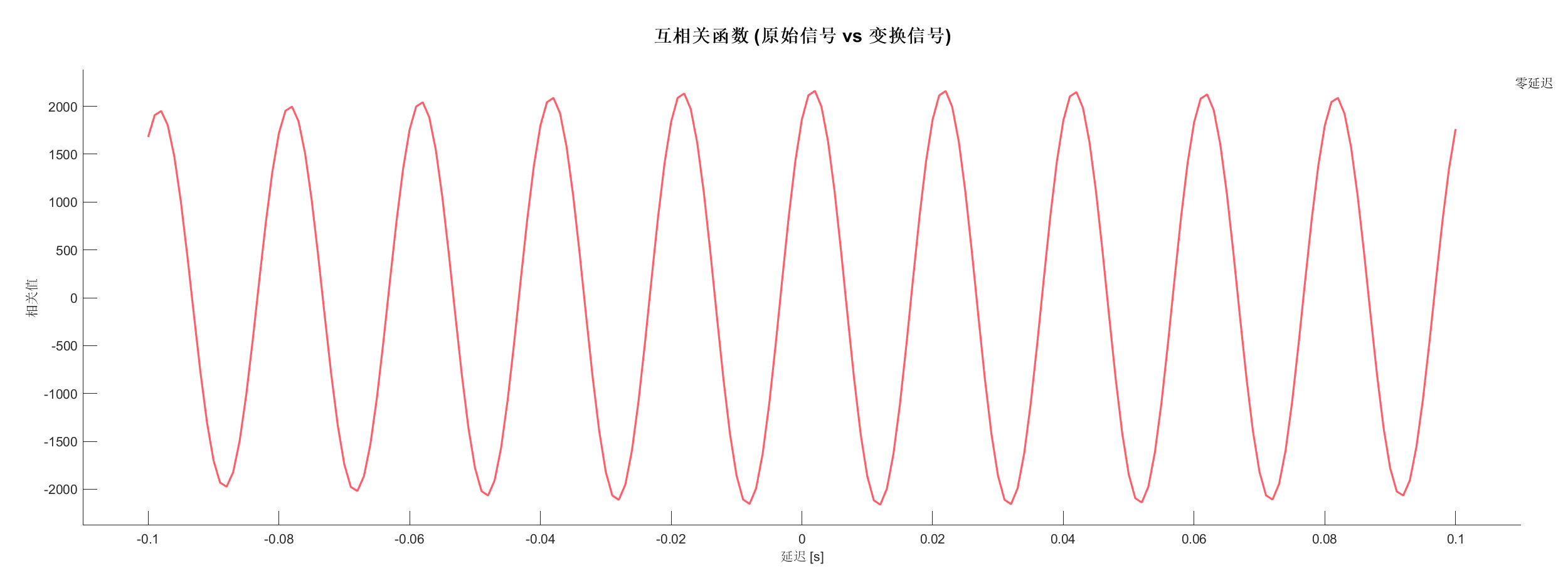
信号内部互相关 - 原始信号与变换信号的互相关
复合信号自相关 - 包含延迟信息的复合信号

图表：

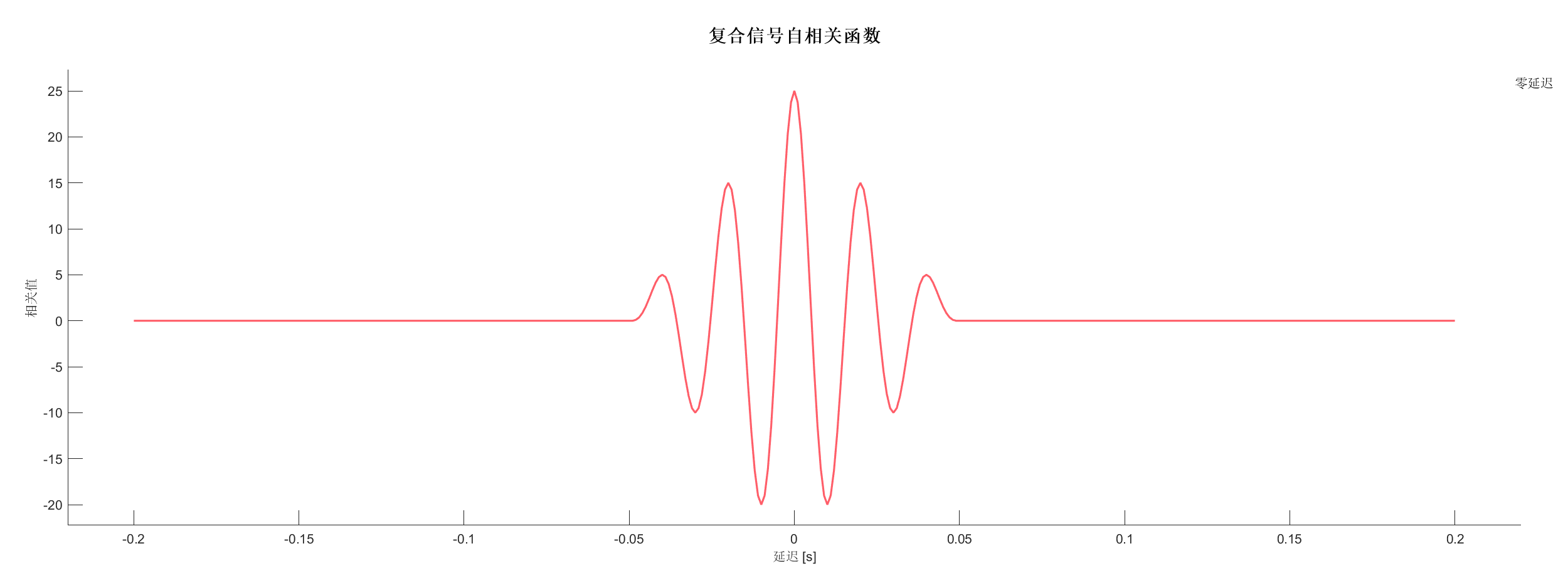
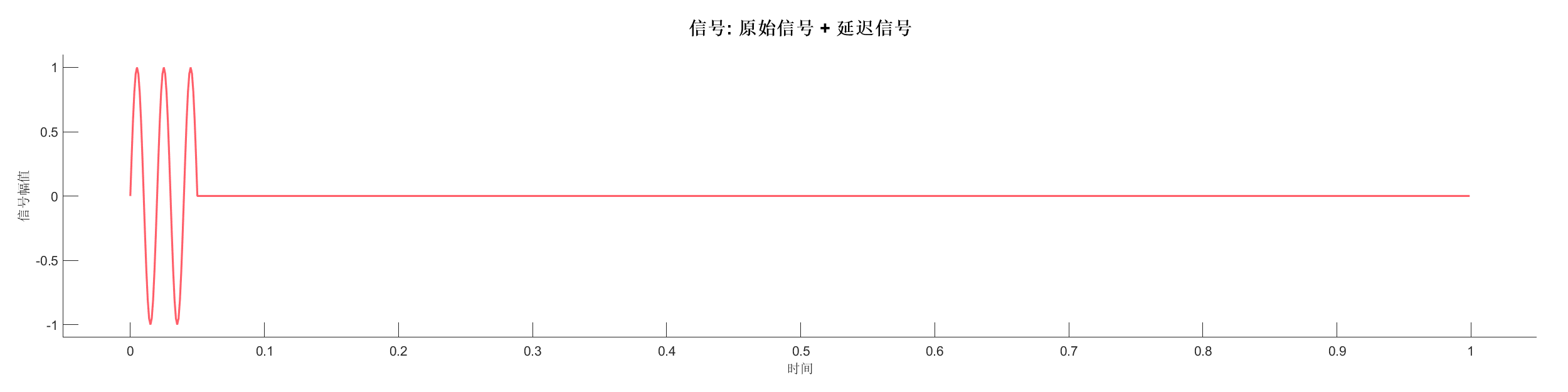
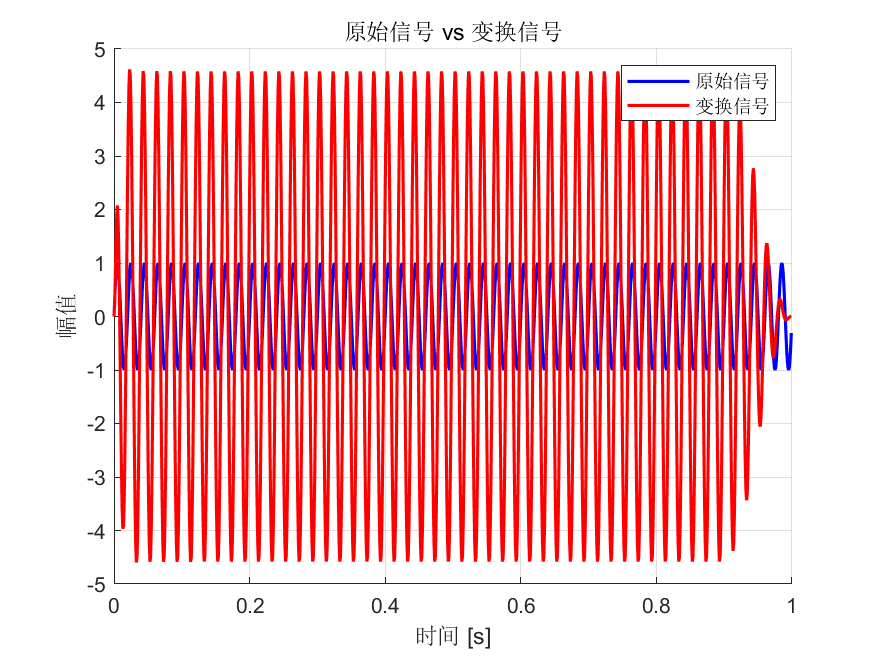
源代码：

%% 案例1: 自相关分析
fs = 1000;
T = 1;
t = 0:1/fs:T-1/fs;
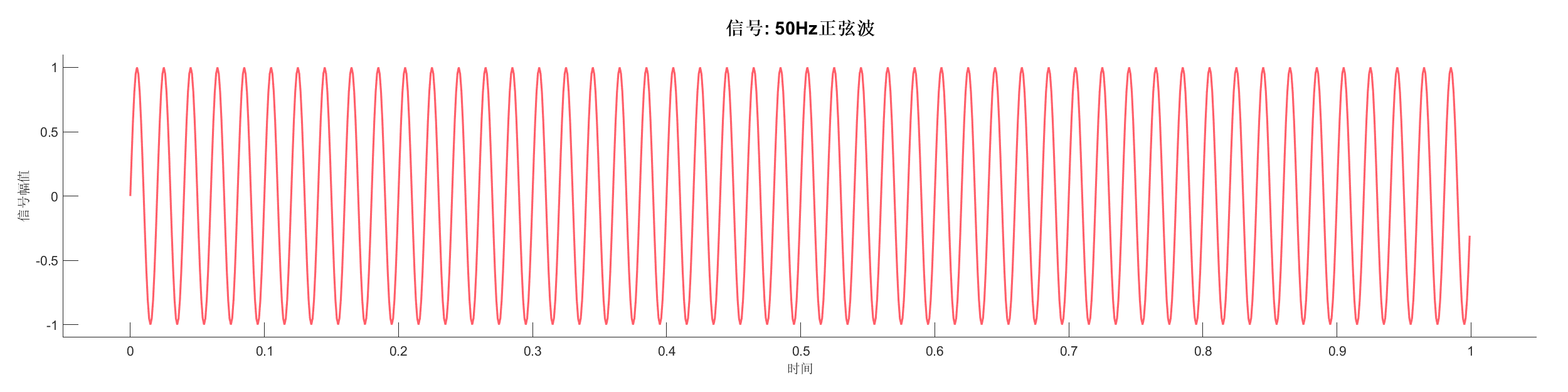
s1 = sin(2*pi*50*t);

inputStruct.t = t;
inputStruct.s = s1;
paramsStruct.Name = 'AutoCorrelation_Demo';
paramsStruct.Echo = 1;

SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();

% 自相关分析 (s1 vs s1)
SA1 = Correlation(SA1, 0, 0);
PlotCor(SA1, 'Title', '自相关函数', 'Geom', 'stem');

%% 案例2: 信号内部互相关
SA2 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA2 = SA2.solve();

% 进行信号变换
SA2 = WaveletTransform(SA2, 'WaveType', 'min', 'fdom', 50);

% 互相关分析 (input.s vs output.s_Transform)
SA2 = Correlation(SA2, 0, 1);
PlotCor(SA2, 'Title', '互相关函数', 'LagRange', [-0.1, 0.1]);

%% 案例3: 复合信号自相关
% 创建包含两个频率成分的复合信号
s3 = s1 + s2;  % 叠加原始信号和延迟信号

inputStruct.s = s3;
paramsStruct.Name = 'CrossCorrelation_Demo2';
paramsStruct.Echo = 1;

SA3 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA3 = SA3.solve();

% 自相关分析
SA3 = Correlation(SA3, 0, 0);
PlotCor(SA3, 'Title', '复合信号自相关函数', 'LagRange', [-0.2, 0.2]);

Demo20 - 功率谱分析

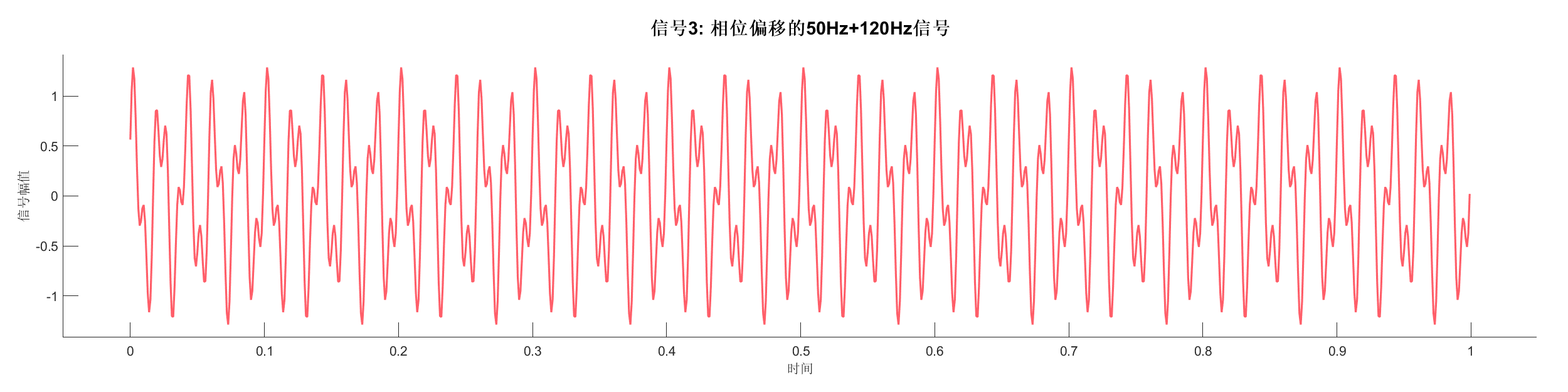
案例介绍：

演示功率谱密度分析的三个场景：

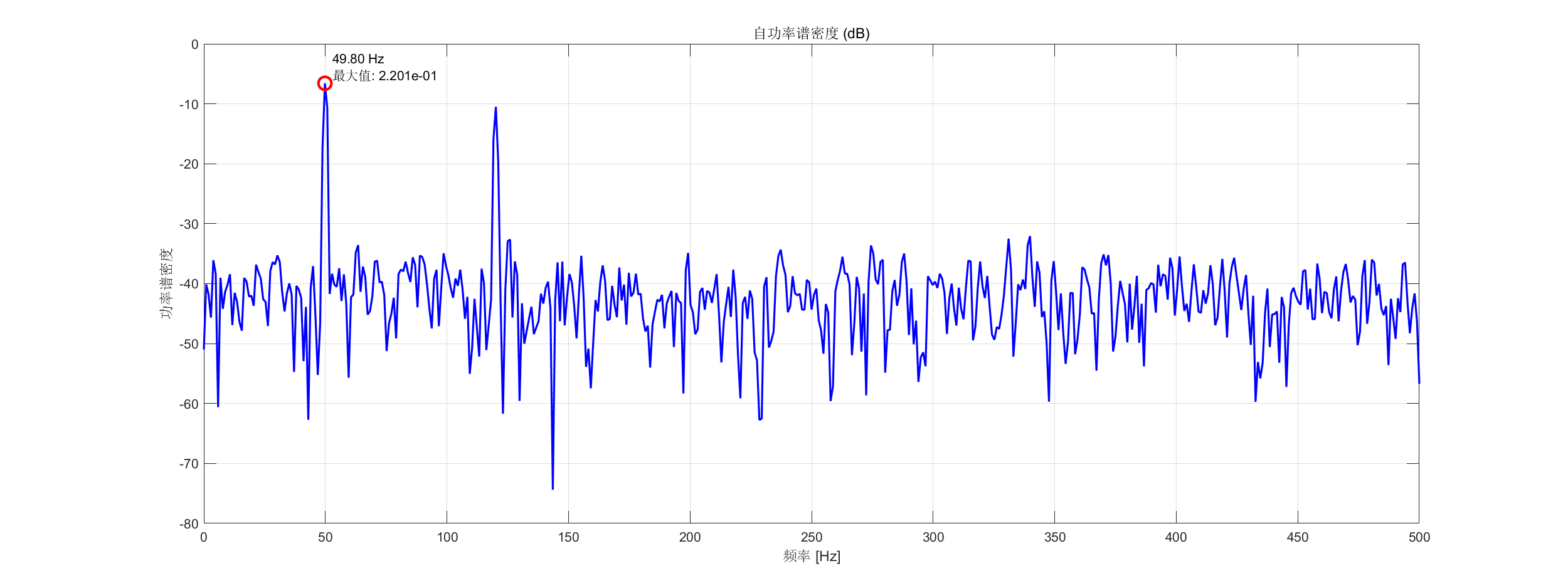
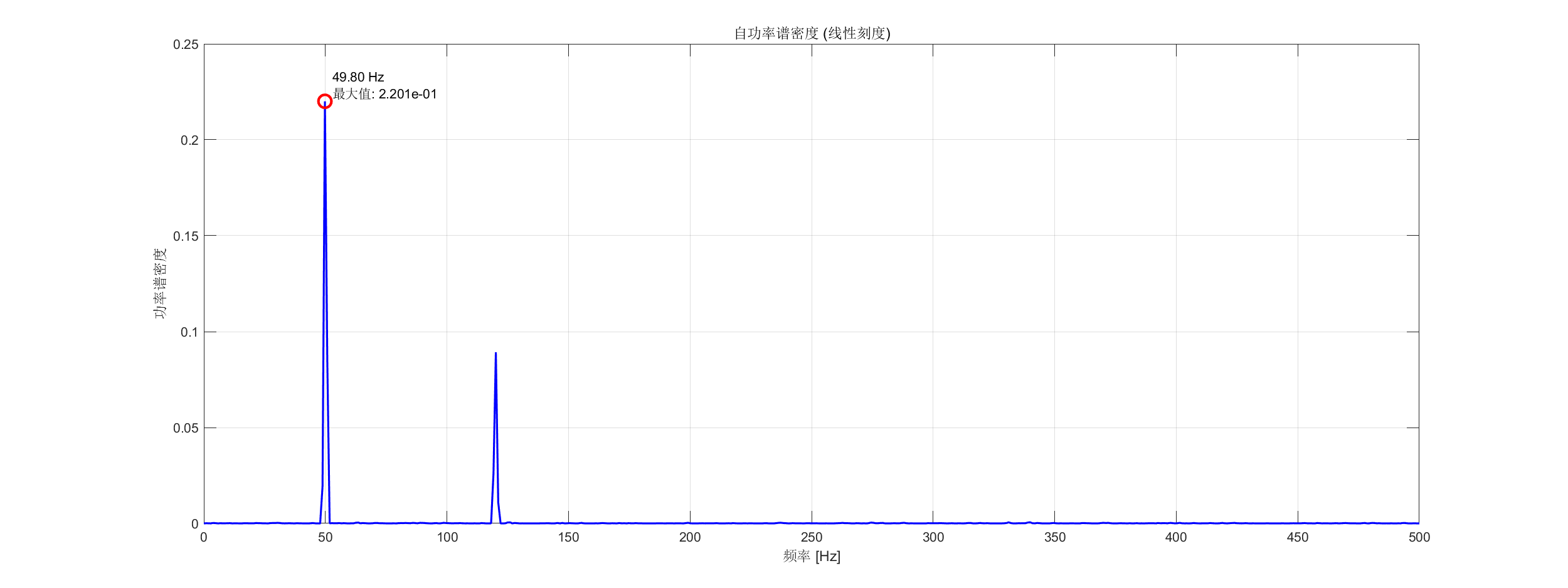
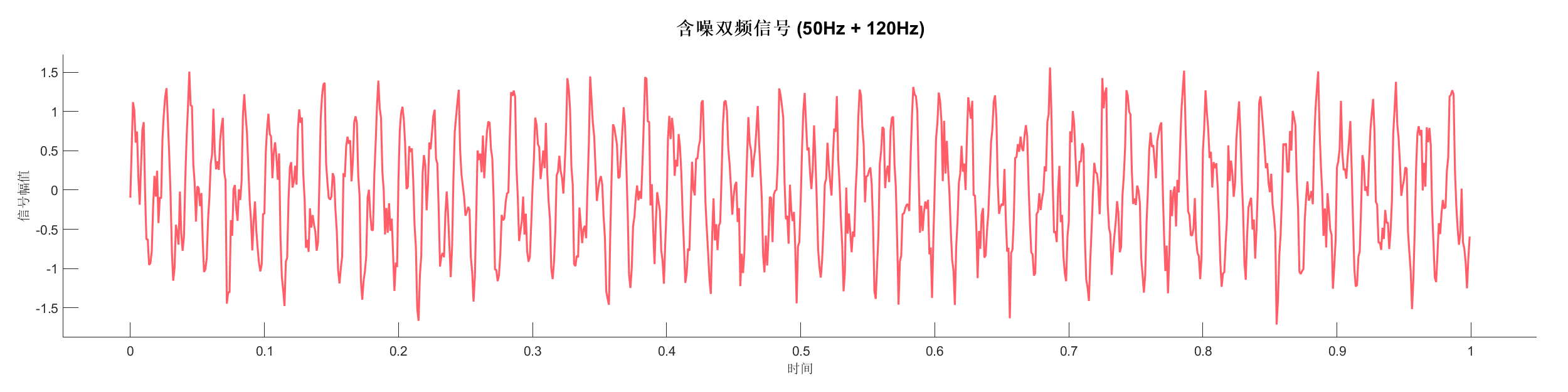
自功率谱分析 - 使用 Welch 方法估计含噪双频信号的 PSD
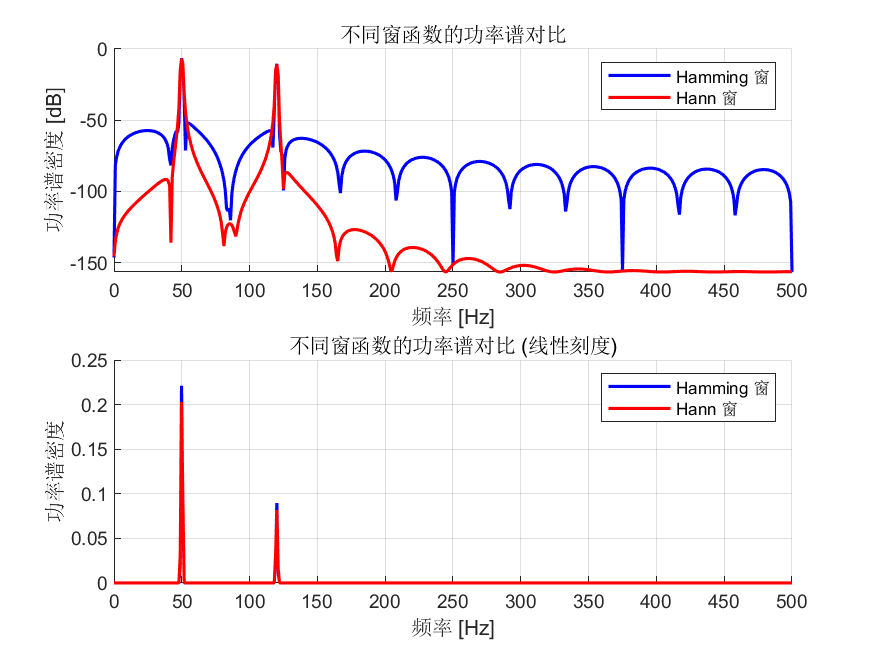
不同窗函数对比 - Hamming 窗和 Hann 窗的效果对比
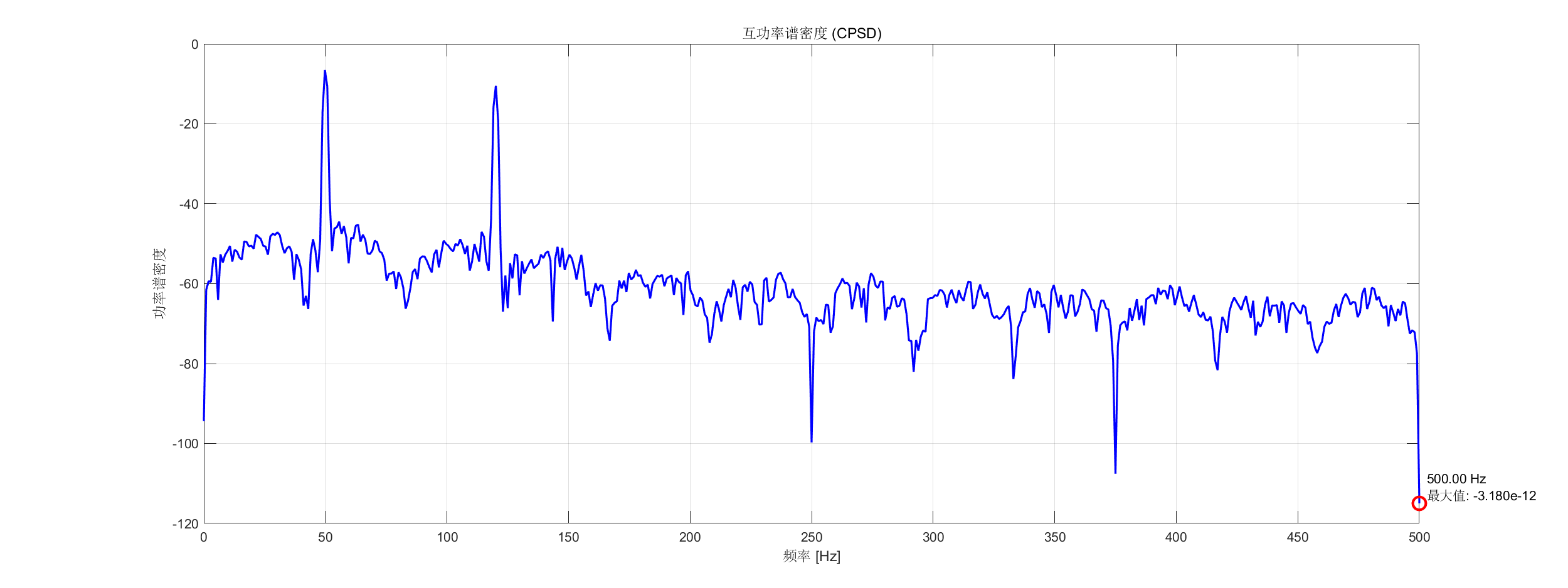
互功率谱分析 - 分析两个相关信号的互功率谱

图表：

源代码：

%% 案例1: 自功率谱分析
fs = 1000;
T = 1;
t = 0:1/fs:T-1/fs;

% 信号1: 包含两个频率成分的信号
s1 = 0.8 * sin(2*pi*50*t) + 0.5 * sin(2*pi*120*t);
s1 = s1 + 0.2 * randn(size(t));  % 添加随机噪声

inputStruct.t = t;
inputStruct.s = s1;
paramsStruct.Name = 'PowerSpectrum_Demo1';
paramsStruct.Echo = 1;

SA1 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1 = SA1.solve();

% 自功率谱分析 (s1 vs s1)
SA1 = PowerSpectrum(SA1, 0, 0, 'Window', 'hamming', 'WindowLength', 1024);

% 绘制线性刻度的功率谱
PlotPowerSpectrum(SA1, 'Title', '自功率谱密度 (线性刻度)', 'YScale', 'linear');

% 绘制 dB 刻度的功率谱
PlotPowerSpectrum(SA1, 'Title', '自功率谱密度 (dB)', 'YScale', 'db');

%% 案例3: 互功率谱分析
% 信号3: 与信号1有相似成分但相位不同
s3 = 0.8 * sin(2*pi*50*t + pi/4) + 0.5 * sin(2*pi*120*t);

inputStruct.s = s3;
paramsStruct.Name = 'PowerSpectrum_Demo3';
SA3 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA3 = SA3.solve();

% 重新创建信号1的对象用于互功率谱
inputStruct.s = s1;
paramsStruct.Name = 'PowerSpectrum_Demo1_2';
SA1_2 = signal.SignalAnalysis(paramsStruct, inputStruct);
SA1_2 = SA1_2.solve();

% 将信号1的数据存到SA3的output中
SA3.output.s_Transform = SA1_2.input.s;

% 互功率谱分析 (input.s vs output.s_Transform)
SA3 = PowerSpectrum(SA3, 0, 1, 'Window', 'hamming', 'WindowLength', 1024);

% 绘制互功率谱
PlotPowerSpectrum(SA3, 'Title', '互功率谱密度 (CPSD)', 'YScale', 'db');

参考文献

[1] MATLAB Signal Processing Toolbox Documentation

[2] Oppenheim, A. V., & Schafer, R. W. (2009). Discrete-Time Signal Processing (3rd ed.). Pearson.

本网站基于Hexo 3-Hexz主题生成。如需转载请标注来源,如有错误请批评指正,欢迎邮件至 392176462@qq.com